“随机数的产生与应用”课堂实录及反思
2013-10-26
●
(温州中学 浙江温州 325014)
“随机数的产生与应用”课堂实录及反思
●孙军波徐芳芳
(温州中学 浙江温州 325014)
“上好一节课好难,上好一节公开课更难”,这是很多一线教师的心声.笔者有幸参加了2012年第6届全国高中青年数学教师优秀课观摩与展示活动,深有体会.大会指定给笔者的课题是“随机数的产生与应用”,以下为笔者在备课和上课过程中的一些想法,敬请大家批评指正!
1 备课困惑
“随机数的产生与应用”即人教版《数学(必修3)》第3章“概率”中“(整数值)随机数的产生”一节.主要内容是借助计算机产生随机数,通过数学建模解决实际问题,让学生体会频率稳定趋于概率的客观规律.这是易被忽视但却极具数学内涵的一节课.学生通过前期学习,已掌握随机事件的概率、古典概型,并且在第2章统计中接触过随机数表.有些学生在计算器中学习过随机函数,因此对学生而言,随机数有点熟悉却还是陌生.根据内容解析和教学任务,本节课的教学目标确定为:
(1)通过对计算机模拟抛硬币问题的解决,运用计算器(机)等信息技术手段,获得计算机模拟抛硬币的试验结果,比较模拟实验结果和科学家物理试验的结果,认识到它们之间的区别和共同之处,体会伪随机数模拟随机数的过程,认识到计算机模拟实际问题的可行性,了解随机模拟的方法:建模——模拟——分析.
(2)通过合理地介绍随机模拟的历史、用途,表达实际问题中引进随机模拟方法的必要性,认识到随机模拟方法的实用性.
(3)经历建立和运用随机模拟方法的过程,初步体验数学建模的基本思想,体会数学的作用与价值,培养分析问题、解决问题的能力.
这部分内容的教学处理,以随机数的产生与应用这一内容为主线,让解决模拟投掷硬币为先导,引入随机数的产生,以天气预报问题为实际应用,将前面已学过的内容及处理问题的思想方法紧密结合起来,使之成为一个整体.因此教学中应当注意贯彻教材的设计意图,让学生经历计算机模拟硬币的全过程,能在这一过程中认识实际问题转化为数学问题的过程,认识计算机模拟的作用,体会随机模拟的思想方法.
结合以上分析,本节课的教学重点为:将实际问题转化为数学模型,在计算机模拟试验的过程中,体会随机数产生的必要性及随机数的实用价值.其中教学最大的难点确定为:如何让学生体会到一个事件的概率与随机数的产生有关,以及数学模型的建立.
根据教学重点和难点,本节课的教学流程主要分为4个环节:群策群力建模型、计算机模拟抛硬币、追溯历史知用途、亲身试验深感受.
2 课堂实录
2.1 课堂教学片断1:群策群力建模型
师:在“随机事件的概率”一节课中,同学们做了大量重复试验,这样做试验很费时间,有没有其他方法可以代替试验呢?
生:用计算机模拟.
师:如何用计算机模拟抛硬币呢?计算机不能像人一样用手去抛硬币,也不能用肉眼来观看结果,那如何用计算机模拟抛硬币呢?
生1:可以规定硬币正面向上为1,反面向上为0,再用计算机随机产生0,1,就可以代替抛硬币.
师(追问):为什么要规定硬币正面为1,反面为0?
生1:因为计算机能处理数字、函数.
师:这是一个划时代的想法,当我们给予试验结果以数字特征后,便实现了计算机模拟的可行性.
师:其实在大家身边的计算器中就存在一个可以随机产生0,1的函数,有没有同学知道?
生2:是ranint函数.
(该生上台操作演示给其他学生看.)
师:随机函数就在大家身边,这样做速度是比手工抛硬币快,但是记录结果还是要依赖手工.其实在Excel中也存在一个函数,叫randbetween(a,b),它可以等可能地返回[a,b]内的任意一个整数.接下来我们一起来用计算机模拟一下.
设计意图通过讨论“如何用计算机模拟抛硬币”,让学生自己给予试验结果以数字特征.因为他们发现只有给予试验结果以数字特征,计算机才好处理,数学建模的思想才能很好地渗透进去.
2.2 课堂教学片断2:追溯历史知用途
通过用Excel模拟抛硬币,获得了一张试验结果的统计图.通过观察发现,计算机模拟的结果与数学家的试验结果基本吻合.在这一环节中,通过众所周知的抛硬币问题肯定了随机模拟方法是可行的、可信的.那随机模拟方法有什么用?是谁发明的?什么才是真的随机数?
其实用计算机随机函数产生的并不是真正的随机数.例如要产生0,1之间的随机整数,我们把2个大小形状相同的小球分别标上0,1放入一个袋中,把它们充分搅拌,然后从中摸出一个,这个球上的数就称为随机数.计算机或计算器上产生的随机数并不是真正的随机数,它们具有类似随机数的性质,我们称为伪随机数.上面用计算机或计算器模拟了掷硬币的试验,我们称用计算机或计算器模拟试验的方法为随机模拟方法或蒙特卡罗方法.
蒙特卡罗方法由在20世纪40年代美国第二次世界大战中研制原子弹“曼哈顿计划”的成员乌拉姆和冯·诺伊曼首先提出.数学家冯·诺伊曼用驰名世界的赌城——摩纳哥来命名这种方法,为它蒙上了一层神秘色彩.在这之前,蒙特卡罗方法就已经存在.1777年,法国数学家布丰提出用投针实验的方法求圆周率π.这被认为是蒙特卡罗方法的起源.
借助计算机技术,蒙特卡罗方法实现了2大优点:一是简单:省去了反复的数学推导和演算过程,使得一般人也能够理解和掌握;二是快速.简单和快速,是蒙特卡罗方法在现代项目管理中获得应用的技术基础.
2.3 课堂教学片断3:亲身试验深感受
通过历史的介绍,一下子点燃了学生的求知欲望.在应用环节,笔者主要解决书上的例题:
天气预报说,在今后的3天中,每一天下雨的概率均为40%,这3天中恰有2天下雨的概率是多少?请你设计一个用随机数模拟的方案.
一下子从抛硬币问题到这个问题难度有点大.硬币只有2个面,学生根据已有的认知水平,容易建立数学模型.但是3天中恰好有2天下雨的问题,它涉及3个随机数,并且概率还是40%,跳跃幅度大.这是本节课的一个教学难点,为此在这个环节中笔者设置了这样一个铺垫:
(1)已知袋中有大小相同的7个黄球和3个红球,假设每个球被摸到都是等可能的,利用随机模拟的方法,估计任取一球得到红球的概率.
生3:将红球标为1,2,3,黄球标为4,5,6,7,8,9,10.用随机函数randbetween(1,10)统计其中1,2,3出现的频率,计算不同次数下的频率,观察红球出现的频率是不是随着试验次数的增加越来越稳定在某个常数附近.
师:非常好!我们不仅可以解决概率为0.5的数学概率模型,还可以模拟其他概率模型,不过这个问题大家用所学过的古典概型即可解决,接下来我们一起来挑战一下.
(2)书本上关于“天气预报”的例题.
经过充分的讨论后,请学生讲解其方案,其他学生进行讨论.
生4:能不能用古典概型来算?排除3天都不下雨、3天都下雨、恰好1天下雨的事件.
生5:不可以,显然由于每天下雨的概率是40%,3天连着下雨和3天都不下雨这2个基本事件不是等可能的,不能用古典概型.
(大家对这位学生的想法表示肯定.)
生6:首先取1~10这10个数字,规定1,2,3,4为下雨,5~10为不下雨,3个随机数为一组,产生数字以后,统计3个数字中恰好有2个小于5的数的组数,根据这个组数除以总数,计算频率,用频率来估计它的概率.
师:好,就按这位同学说的,大家试试看.
(教师强调试验的各项条件,试验后汇总数据,如图1所示.)

图1
师:就目前的结果而言,频率有没有出现稳定,那我们应该怎么办?
(有学生点头,有学生摇头.)
生(众):增加试验次数.
借助Excel绘制得到如图2的统计图:
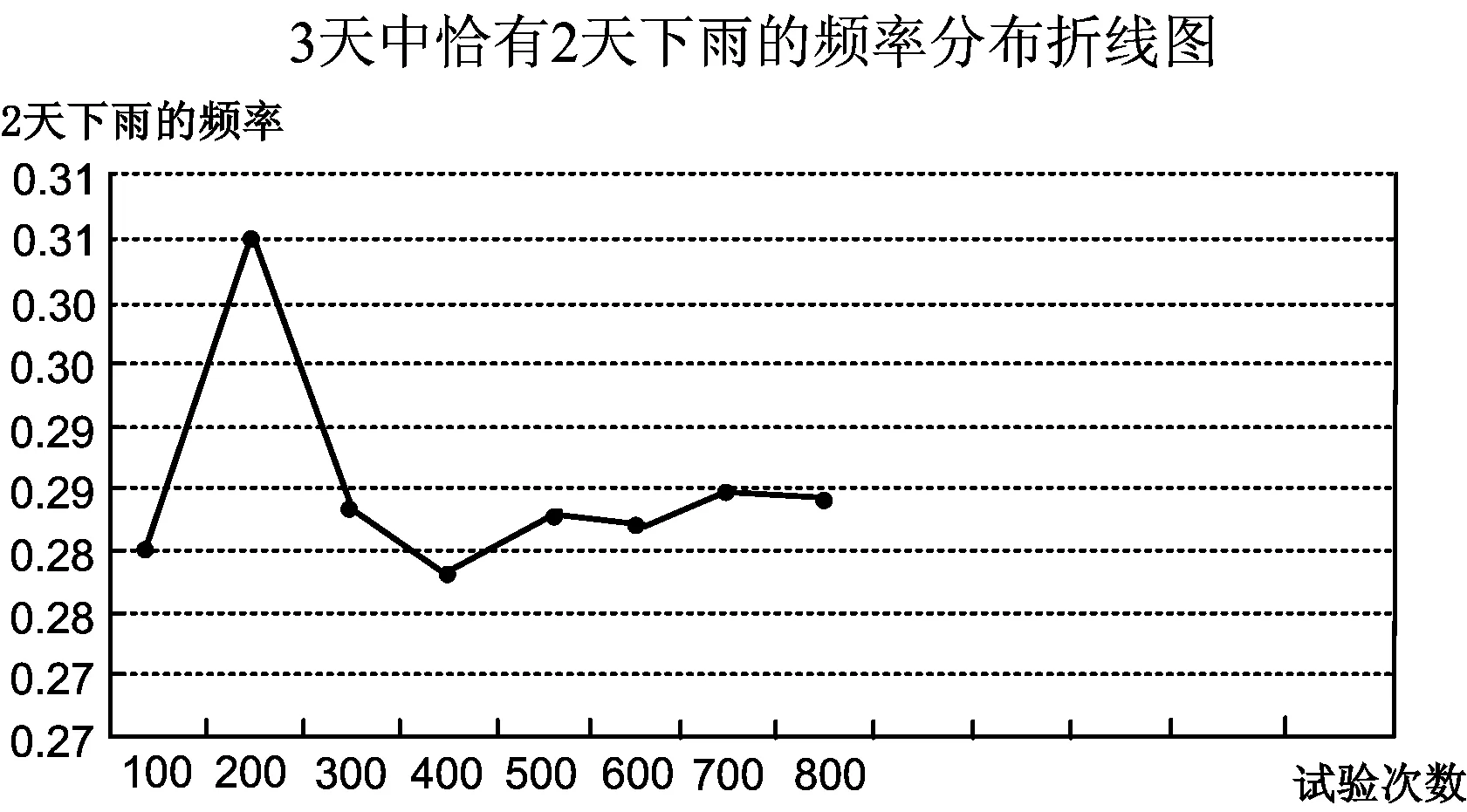
图2
通过观察发现,随着试验次数的增加,频率大约稳定在0.29.至此学生发现蒙特卡罗方法还可以解决一些更为复杂的概率问题.
3 专家点评
本课例是笔者参加第6届全国高中青年数学教师优秀课观摩与展示活动,为大会指定的课题.组委会聘请了全国知名的教授作为评委,因此本课有幸得到了几位专家的点评和意见.他们提出的许多宝贵且具有深远意义的意见和建议,也引发了笔者更多、更深的思考.整理如下:
3.1 活用教材
备好一节课,首先应该要用好教材,教材理解深刻、到位,才能出好课.情境创设要接近生活,不可脱离实际,不要为了创设而有情景,合理的情景创设可以更好地激发学生的兴趣;问题设置必须清晰合理,好的问题可以引领着学生去思考,帮助学生理解概念;信息技术的有机融合,就像本课对信息技术的处理非常好,随机数要用Excel来产生.教师如果把握不好,极易把数学课变成信息课,使得学生的兴奋点停留在计算机上,更会淡化数学味道,因此对教材一定要理解到位;数学应该提供思想,提供建模的思想,信息技术是辅助我们实现想法的工具;数学文化的渗透非常必要,在了解蒙特卡罗方法历史的环节中,学生兴奋的表情表达了他们极大的求知欲望,这也是教材把历史背景放在其中的重要原因.
3.2 尊重学生
课堂教学一定要注重学生活动与自主探究,学生有没有动起来是非常重要的.比如在随机数应用的环节,让学生讨论,学生间的讨论代替了传统教师的评价,使得学生更容易发现以目前的古典概型知识较难解决天气预报问题,在学生成功提出方案后,让所有的学生参与进来,更加体现出数据的随机性和真实性,让学生亲身经历了模型的建立,数据的产生与处理,试验结果的分析,成功渗透了数学建模思想.很多时候,教师担心学生讲不好,着急地越俎代庖,这样做的效果并不是真正的有效教学,学生亲历的往往是他印象最深的,因此个别环节教师甚至可以更大胆地放手.
4 自我反思
在听完教授的分析点评后,笔者思考良久,多次的磨课经历涌上心头,有2点感悟特别深刻:
(1)备一节课好难,但是好课就在身边.刚开始备这节课时,感觉不知从何挖掘.因为这是一节对信息技术依赖比较大的课,所以易被大家所忽视.通过长时间的磨课后,笔者发现这是一节非常具有数学内涵的课,它的核心内容是用计算机产生随机数,帮助解决更复杂的概率问题.首先通过硬币试验需要耗时耗力提出问题,在借助计算机解决模拟抛硬币问题的同时,发现计算机模拟的结果与科学家手工试验的结果基本吻合,肯定了蒙特卡罗方法是可行的、可信的.其次利用随机数解决目前古典概型相对难解决的天气预报问题,使学生再次回顾了利用频率来估计概率的大数定律.而整个问题的解决过程不就是一个数学建模过程吗?这节课不就是一个数学知识实际应用问题吗?教材需要我们好好去思考和挖掘,好课的发现需要我们好好再去思考一下.
(2)“尊重学生,以人为本”不能只停留在口号上.当课堂变得无趣,学生变得不配合时,也许可以考虑一下,我们是不是真的尽力了.笔者在磨课过程中,就曾经遇到学生冷场的情况.回头想想,其实是当时的问题设计得不够到位,不能真正地引发学生的思考,有些时候是自己拼命地讲,学生只好乖乖地等着、瞪着.尊重学生,尊重学情,好的课堂才会自然而来.
