与数论有关的竞赛题类型探究
2013-10-26
●
(元培中学 浙江绍兴 312000)
与数论有关的竞赛题类型探究
●章国水
(元培中学 浙江绍兴 312000)
初等数论问题是数学竞赛的热点内容,它所涉及的范围主要有十进制整数及表示方法、奇数和偶数、整除性(被2,3,4,5,8,9,11等数整除的判定)、素数和合数、最大公约数与最小公倍数、带余除法、同余、完全平方数、不定方程等等.初等数论问题在初中数学竞赛中占有较大比例,本文通过对全国各地初中数学竞赛中的有关初等数论的试题进行研究,结合一些有关数论的竞赛试题进行题型及解法介绍.
1 奇偶性分析
自然数可以分为奇数和偶数.对于奇数与偶数的性质,在解答竞赛题时只要合理、灵活、巧妙、有意识地利用它并运用正确的推理分析方法,就可以解决许多与奇偶数相关的有趣问题.
例1将1,2,3,4,5这5个数字排成一排,最后一个数是奇数,且使得其中任意连续3个数之和都能被这3个数中的第1个数整除,那么满足要求的排法有
( )
A.2种 B.3种 C.4种 D.5种
(2008年数学周报杯全国初中数学联赛试题)
解设a1,a2,a3,a4,a5是1,2,3,4,5的一个满足要求的排列.
首先,对于a1,a2,a3,a4,不能有连续的2个数都是偶数,否则,这2个数之后都是偶数,与已知条件矛盾.
又如果ai(1≤i≤3)是偶数,ai+1是奇数,则ai+2是奇数,这说明一个偶数后面一定要接2个或2个以上的奇数,除非接的这个奇数是最后一个数.
因此a1,a2,a3,a4,a5只能是:偶,奇,奇,偶,奇,有如下5种情形满足条件:2,1,3,4,5;2,3,5,4,1;2,5,1,4,3;4,3,1,2,5;4,5,3,2,1.故选D.
2 带余除法
给定整数a,b,b≠0,如果有整数q,r(0≤r<|b|)满足a=qb+r,则q和r分别称为a除以b的商和余数.特别地,当r=0时,称a被b整除,记作b|a,或者说a是b的倍数,而b是a的约数.
2.1 整除
例2小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我2元,我的钱数将是你的n倍”;小玲对小倩说:“你若给我n元,我的钱数将是你的2倍”,其中n为正整数,则n的可能值的个数是
( )
A.1 B.2 C.3 D.4
(2012年数学周报杯全国初中数学联赛试题)
解设小倩所有的钱数为x元、小玲所有的钱数为y元,均为非负整数.由题设可得
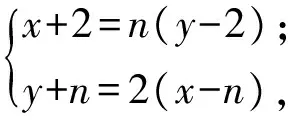
消去x得
(2y-7)n=y+4,
则
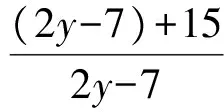

2.2 约数与倍数
例3对于i=2,3,…,k,正整数n除以i所得的余数为i-1.若n的最小值n0满足2 000 (2010年数学周报杯全国初中数学联赛试题) 解因为n+1为2,3,…,k的倍数,所以n的最小值n0满足n0+1=[2,3,…,k],其中[2,3,…,k]表示2,3,…,k的最小公倍数.由于 [2,3,…,8]=840,[2,3,…,9]=2 520, [2,3,…,10]=2 520,[2,3,…,11]=27 720, 因此满足2 000 素数、合数与完全平方数都是比较特殊的整数,在竞赛中常常可以看到关于这类数的问题.只要抓住这些数的特性,问题就迎刃而解.如完全平方数的特性,奇数的平方是8n+1型;偶数的平方为8n或8n+4型. 3.1 素数与合数 例4设p(≥5)是质数,并且2p+1也是质数.求证:4p+1是合数. 证明由于p是大于3的质数,故p不会是3k的形式,从而p必定是3k+1或3k+2的形式,k是正整数. (1)若p=3k+1,则 2p+1=2(3k+1)+1=3(2k+1) 是合数,与题设矛盾. (2)若p=3k+2,这时 4p+1=4(3k+2)+1=3(4k+3) 是合数.故4p+1是合数. 3.2 完全平方数 例5能使2n+256是完全平方数的正整数n的值为______. (2011年全国初中数学联赛试题) 解当n<8时,2n+256=2n(1+28-n),若它是完全平方数,则n必为偶数. 若n=2,则2n+256=22×65; 若n=4,则2n+256=24×17; 若n=6,则2n+256=26×5; 若n=8,则2n+256=28×2. 因此,当n≤8时,2n+256都不是完全平方数. 当n>8时,2n+256=28(2n-8+1), 若它是完全平方数,则2n-8+1为一奇数的平方.设2n-8+1=(2k+1)2(k为自然数),则 2n-10=k(k+1). 由于k和k+1是一奇一偶,因此k=1,于是2n-10=2,故n=11. 对于整数a,b,c,且c≠0,若c|(a-b),则称a,b关于模c同余,记作a≡b(modc),比如26≡14(mod12). 例6设n为整数,且1≤n≤2 012.若(n2-n+3)(n2+n+3)能被5整除,则所有n的个数为______. (2012年数学周报杯全国初中数学联赛试题) 解(n2-n+3)(n2+n+3)= (n2+3)2-n2= n4+5n2+9, 可知5|(n4+9),从而n4≡1(mod5),于是 n=5k±1或n=5k±2, 又 2 012÷5=402……2, 因此共有2 012-402=1 610个数. 不定方程也称为丢番图方程,是数论的重要分支学科,也是历史上最活跃的数学领域之一.数学竞赛中的不定方程问题,不仅要求学生对初等数论的一般理论、方法有一定的了解,而且讲究思想、方法与技巧,要求创造性地解决问题. 例7已知直角三角形的边长均为整数,周长为60,求它的外接圆的面积. (2012年全国初中数学联赛试题) 解设直角三角形的3条边长分别为a,b,c(a≤b a+b+c=60. 显然,三角形的外接圆的直径即为斜边长c,下面先求c的值.由a≤b 60=a+b+c<3c, 从而 c>20. 由a+b>c及a+b+c=60,得 60=a+b+c>2c, 从而 c<30. 又因为c为整数,所以21≤c≤29.根据勾股定理可得 a2+b2=c2, 把c=60-a-b代入,化简得 ab-60(a+b)+1 800=0, 即 (60-a)(60-b)=1 800=23×32×52. 因为a,b均为整数且a≤b,所以只可能是 或 解得 高斯函数是一个非常重要的数论函数,其应用非常广泛.在数学竞赛中经常出现关于[x]的方程、等式、不等式、整除问题、格点问题、组合数问题等.对任意实数x,[x]是不超过x的最大整数.亦称[x]为x的整数部分,[x]≤x<[x]+1. (2006年全国初中数学联赛试题) 因此 故 18≤30<19, 例9小明家电话号码原为6位数,第1次升位是在首位号码和第2位号码之间加上数字8,成为一个7位数的电话号码;第2次升位是在首位号码前加上数字2,成为一个8位数的电话号码.小明发现,他家2次升位后的电话号码的8位数,恰是原来电话号码的6位数的81倍,则小明家原来的电话号码是______. (2006年全国初中数学联赛试题) 记x=b×104+c×103+d×102+e×10+f,于是 81×a×105+81x=208×105+a×106+x, 解得 x=1 250×(208-71a). 因为 0≤x<105, 所以 0≤1 250×(208-71a)<105, 故 因为a为整数,所以a=2,于是 x=1 250×(208-71×2)=82 500. 因此,小明家原来的电话号码为282 500. 这类竞赛题所涉及到的数论知识比较多,要结合以上几种类型的方法进行解决. 例9如果对一切x的整数值,x的二次三项式ax2+bx+c的值都是平方数(即整数的平方).证明: (1)2a,2b,c都是整数; (2)a,b,c都是整数,并且c是平方数; (3)反过来,如果第(2)小题成立,是否对一切的x的整数值,x的二次三项式ax2+bx+c的值都是平方数? (2002年全国初中数学联赛试题) 证明(1)由题设,分别令x=0,-1,1,可得c=m2,2a=n2+k2,2b=n2-k2均为整数(其中m,n,k为整数). (2)第(1)小题中已证c是整数且是平方数. 假设2b为奇数2t+1(t为整数),取x=4得16a+4b+m2=h2(h为整数).因为2a为整数,从而16a可被4整除,故16a+4b=16a+4t+2除以4余2,所以16a+4b为偶数.又因为 16a+4b=(h+m)(h-m). 若h,m的奇偶性不同,则 16a+4b=(h+m)(h-m) 为奇数,这与16a+4b为偶数矛盾. 若h,m的奇偶性相同,则 16a+4b=(h+m)(h-m) 能被4整除,从而2b为偶数,这与假设矛盾. 因此假设不成立,即2b应为偶数,b为整数,故a=k2+b-c为整数. (3)令a=b=c=x=1,则ax2+bx+c=3,不是平方数,因此不一定成立.3 素数、合数与完全平方数
4 同余
5 不定方程
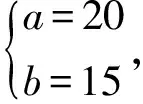

6 高斯函数
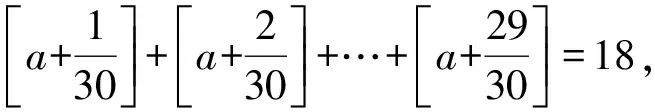


7 进位制



8 综合型
