基于LZW算法的声波测井数据压缩研究

邹学玉，冯振，张少华，韩付伟

（长江大学电子信息学院，湖北 荆州 434023）

0 引 言

目前，井下传输系统的带宽扩容速度远远不及声波测井数据的增长速度，且传输系统的带宽不可能无限制增长。因此，必须对井下声波测井数据进行压缩。不少的研究方法都是基于软件压缩，其缺点是压缩速度慢，不适用于对大量数据进行实时压缩。压缩数据总目标是要减少容纳给定消息集合的信号空间。存储空间的减少意味着传输效率的提高和占用频带的节省，这就提高了在有限传输带宽的情况下测井数据的传输效率。目前对声波测井数据的压缩方法：有损压缩算法预测编码与小波变换相结合［1］；SPIHT 算法［2］；FLAC 算法；APE 算法［11］；帧相关压缩算法［3］；LZW 压缩方法［4］等。但上述不少编码是基于数据源的统计概率特性和软件的。基于统计概率的信源编码是Shannon信息论的基本特征，但是在某些需要实施压缩的场合，要确定实际信源的统计特性相当困难。

本文提出了引入哈希函数的LZW算法，它是基于数据串特性的编码方法，不依赖于信源统计特性的编码方法称为通用码［5］。LZW是基于字典的无损压缩编码，试验证明，LZW算法和Hash函数相结合，不仅压缩效率高，而且易于用硬件实现。

1 LZW算法

LZW是一种基于字典的算法。所谓字典算法，即认为信源输出的信息序列是由一本字典中的各种词条构成的。显然，该字典的词条应由信源符号的不同排列组合产生。但该字典不是固定不变，而是根据信源发出的编码动态建立。编码过程也就是建立字典的过程。如果接收端建立的字典与发送端一样，就达到了正确的信息传送目的。

LZW算法是Terry A.Welch 1984年在LZ78的基础上加以改进提出来的［6］。该算法速度快，压缩率高，最重要的是不需要知道待压缩数据的概率统计特性。LZW算法通过字典，把输入的字符串映射成等长码字输出。LZW算法的字典具有前缀特性，这样就使得任何一个字典中的字符串的前缀也一定在字典中。例如：如果一个字符串是WK，其中W是一个字符串，K是单个字符，如果WK在字典中，那么W也一定在字典中。

LZW算法对每个输入字符串进行逐个字符检查，试图找到最长的和字典已有字符串匹配的字符串并进行解析，这样字典内的编码项会越来越多，匹配几率也会随之增大，从而达到压缩目的。每个被解析了的字符串通过下一个输入字符扩展，这样形成的新字符串会被存入字典，新字符串会有一个新的标示符，称为编码值，并且同时输出前缀码也就是W的编码值［6］。LZW编码流程见图1。

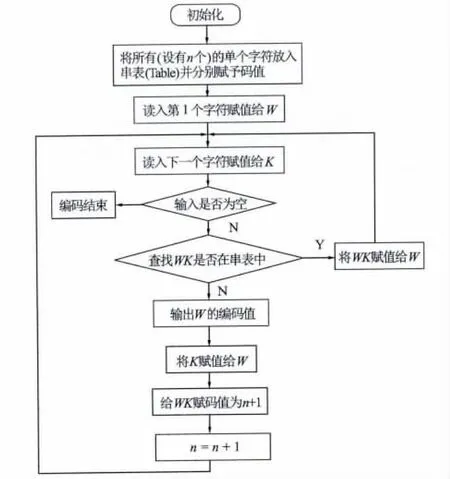
图1 LZW算法流程图

2 Hash函数

由于传统LZW算法每次需要查找当前词条是否与字典已有词条匹配，如果对逐个词条进行查找，查找效率势必非常低，从而影响压缩速率。因此，本文引入了Hash函数，利用哈希查找，只要根据对应函数找到给定值K的像h（K）。若结构中存在关键字和K相等的记录，则必定在h（K）的存储位置上，由此，不需要进行比较便可直接取得所查记录。在此，称这个对应关系h为哈希（Hash）函数，据此建立的表为哈希表（Hash table）。

然而，对不同关键字可能得到同一哈希地址，即key1≠key2，而h（key1）＝h（key2），这种现象称冲突（collision）。因此，在建造哈希表时不仅要设定一个哈希函数，而且要设定一种处理冲突的方法［7］。

假设消息M的长度是L。将M分成为n位的块，其中n≪L，p＝［L／n］，则M＝（m1，m2，…，mp），mj表示第j块，其中mp块不足n位用0填充。

将第j块mj写成行向量

式中，mji是一个位。将这些向量堆放在一起形成一个矩阵。散列函数h（M）输出n位，第i位是将矩阵的第i列的所有位进行异或得到的，即ci＝m1i⊕m2i⊕…⊕mli可以表示为

因此，在本文中实际用于压缩的哈希函数采用移位和基本算数运算构造，这样使得哈希函数不仅运算速度快，易于实现，而且从理论上证明了比特之间的异或运算和位移运算能够提高哈希值的随机特性［8］。哈希函数如式（3），其中code表示当前字符，pre＿code表示前缀字符（串）［9］。

为了减少哈希函数冲突的发生，在实际压缩时定义了一个偏移量，通过探测再散列来解决哈希函数的冲突问题。

3 压缩测试及结果分析

3.1 Hash函数测试结果

本文从哈希值的期望、方差、非空桶深期望、非空桶深方差、ASL（平均查找长度）、最大桶深、空桶率、冲突率［10］等方面对哈希函数的性能进行了测试，测试结果如表1至表3所示。

表1 字典深度为512B

表2 字典深度为1kB

表3 字典深度为1kB，并加入偏移量减少哈希冲突

从表1至表3可以看出，在字典深度一定的情况下，哈希值期望、方差、非空桶深期望、非空桶深方差与输入词条数目的关系不大，且比较稳定，说明所测试的异或哈希函数散列性能好。ASL在字典深度不变的情况下，随着输入词条数目的增加略微增加，但均不超过2，说明字典的查找效率高。通过最大桶深可以确定字典在冲突发生几次后清空字典。

最后从空桶率和冲突率可以看出，冲突率是随着字典深度的增加而减小，随着输入词条数目增加而增加的，但如果输入词条数太少，就会使得字典的利用率降低，通过统计测试一般输入词条数一般控制在字典深度的70%～75%。这样既能保证空桶率低于50%，又能保证冲突率低于20%。

3.2 数据压缩测试结果

本文测试的是井下声波测井数据，共有4大帧数据，每大帧数据对应1个深度点的4道波形数据。数据格式为16进制数。文件为AcData.txt，文件大小为32kB（32 802B）。

压缩率＝压缩后数据字节数／压缩前数据字节数，本文中压缩前数据为32 802B，为了节省存储空间，字典深度为512B，压缩后数据为16 460B，经计算压缩率为50.18%，在压缩率方面要比算术编码的压缩率80%左右，预测编码的压缩率70%～90%提高不少［11］。

4 结束语

针对声波测井数据压缩提出无损压缩方法，不仅压缩效率理想，易于软硬件实现，而且LZW和哈希函数的结合可以独立于信源的统计特性，实现实时无损压缩。该方法为硬件压缩系统的实现提供了参考，在测井数据大幅增长的情况下具有很好的应用前景。

［1］李传伟，慕德俊，李安宗，等.随钻声波测井数据实时压缩算法 ［J］.西南石油大学学报，2008，30（5）：81-84.

［2］张伟，师栾兵.声波测井数据压缩的一种SPIHT改进算法 ［J］.电子测量与仪器学报，2008，22（1）：15-19.

［3］汉泽西，郭枫，秦李颗.一种基于测井数据特征的无损压缩方法 ［J］.西安石油大学学报，2006，21（1）：61-63.

［4］刘付斌，李艾华.偶极子数字阵列声波测井仪中数据压缩的实现 ［J］.设计与研发，2007，12：58-61.

［5］Knuth D E.The Art of Computer Programming，volume 1／Fundamental Algorithms；volume3／Sorting and Searching［M］.USA：Addison-Wesley，1973.

［6］Welch T A.A Technique for High-performance Data Compression［J］.IEEE Computer，1984，17（6）：8-18.

［7］Wade Trappe，Lawrence C Washington.Introduction to Cryptography with Coding Theory：Second Edition［M］.USA：Pearson Education，Inc.，publishing as Prentice Hall，2002.

［8］程光，龚俭，丁伟，等.面向IP流测量的哈希算法的研究 ［J］.软件学报，2005，16（5）：652-658.

［9］Li Leiding，Ma Tiehua.FPGA-based Implementation of LZW Algorithm ［J］.Electronic Measurement Technology，2008，31（10）：170-172.

［10］林亚平.异或哈希函数查找中文词组性能评价 ［J］.中文信息学报，1995，9（1）：42-48.

［11］贾安学，乔文孝，鞠晓东，等.声波测井井下数据压缩算法压缩效果测试 ［J］.测井技术，2011，35（3）：288-291.