高效的top-k相似字符串查询算法
2014-01-01陈子阳韩玉俊王璿周军锋
陈子阳,韩玉俊,王璿,周军锋
(1. 燕山大学 信息科学与工程学院,河北 秦皇岛 066004;2. 河北省计算机虚拟技术与系统集成重点实验室,河北 秦皇岛 066004)
1 引言
top-k字符串相似性查询在很多领域有重要应用,如数据清洗、数据集成、生物信息学和模式识别等。一个典型的例子是对文本进行拼写检查时,spellchecker需要从词典库里查找k个与用户输入最相似的单词[1]。在生物信息领域,字符串相似性查询用来找到 top-k相似基因序列,用于疾病预测和新药品研发[2]。数据清洗会从一个实体集合找到top-k个与给定实体最相似的实体[1]。
已有的基于阈值的字符串相似性查询方法[1,3~5]需要用户提前指定相似性函数(如编辑距离)和阈值,然后返回与查询字符串相似性以及在给定阈值内的字符串。当应用该方法求解 top-k相似字符串时,用户很难提前确定一个合适的阈值,当返回结果为空或者返回大量结果时,需要多次根据不同的阈值重复计算,查询效率低。文献[6]使用Trie树索引来组织集合中的所有字符串,通过递增的方式计算查询字符串与Trie树节点所对应的字符串之间的编辑距离来求解top-k结果,由于Trie树节点所对应的字符串仅是字符串集合中字符串的前缀,当字符串长度变大时,由于长字符串的公共前缀较短,该方法会处理很多不相似字符串的前缀,导致系统性能下降。
针对已有方法在求解 top-k相似字符串时效率低的问题,提出了一种长度跳跃索引以及基于该索引的长度过滤策略和计数过滤策略,用以减少需要处理的字符串数量;提出无匹配特征的字符串之间的编辑距离下界,用以进一步减少需要处理的候选字符串数量。基于以上策略,提出了相应的 top-k字符串相似性查询算法,并在不同特征的数据集上进行实验,实验结果验证了本文算法的高效性和扩展性。
2 背景知识
2.1 问题定义
用Σ表示一个有限字符的集合,字符串s可以看成由Σ中字符组成的有序序列,|s|表示字符串s的长度。
现有广泛使用的衡量字符串相似性的标准之一是编辑距离[1~8]。2个字符串的编辑距离是将一个字符串转换成另一个字符串所需要的最少单字符编辑操作次数,允许的单字符编辑操作有:插入、删除和替换。符号ed(r,s) 表示字符串r和s之间的编辑距离。假设r=“srajit”,s=“seraji”,则ed(r,s) = 2表示将字符串“srajit”变为“seraji”所需的最少单字符编辑操作次数为2。
问题定义(top-k字符串相似性查询):给定字符串集合S和查询字符串σ,top-k字符串相似性查询返回集合R⊆S,其中|R|=k,且对∀r∈R和∀s∈S-R,有 ed(r,σ) ≤ ed(s,σ)。
例1表1是字符串集合S中的字符串,假定查询字符串σ=“geometric”,top-3 字符串相似性查询返回的结果R={“geometrics”,“isometric”,“biometric”},σ与这3个字符串的编辑距离分别是1、2、2,集合中其他字符串与σ的编辑距离都不小于2。

表1 字符串集合S中的字符串
2.2 基本概念
q-gram和q-chunk:q-gram 是字符串中所有长度为q的子串,gq(s)表示字符串s的q-gram集合,为保证s中每个字符都有对应的q-gram,需要在字符串s结尾添加q-1个$字符。q-chunk是指字符串中长度为q且起始位置为iq(i≥ 0)的子串,字符串s的q-chunk集合是对s完整且不相交的划分,用cq(s)表示。为了保证字符串最后一个q-chunk有q个字符,需要在s结尾添加(q-(|s|%q))%q个$字符。以字符串“genetic”为例,q= 2,gq(“genetic”) ={“ge”,“en”,“ne”,“et”, “ti”, “ic”,“c$”},cq(“genetic”) = {“ge”,“ne”,“ti”,“c$”}。
字符串s的任意q-gram和q-chunk都称为s的特征(signature)。由于直接计算字符串之间的编辑距离代价较高,已有方法[1,3,5,8~12]在计算与给定查询串相似的字符串时,第一步通过字符串特征进行过滤,以便缩小候选字符串的数量,进而降低第二步编辑距离计算的代价。
为了在第一步执行过滤,文献[1,4,5,8~10,13,14]都会为字符串集合中的所有字符串特征(q-gram)建立倒排表。倒排表中的每个元素是一个二元组<id,pos>,其中id表示相应的q-gram在id对应的字符串中出现,pos表示相应的q-gram在该字符串中出现的起始位置。每一个倒排表按照id升序有序,其中id值相等的元组按照pos升序有序。预处理时,可以按照字符串的长度排序,进而设定每个字符串的id,因此本文的后续讨论中,id小的字符串长度也较短。图1展示了表1中字符串集合的部分q-gram对应的倒排表。对于q-gram =“eo”,由图1可知,“eo”在字符串s3、s6、s7中出现,且起始位置都是1。
2.3 相关工作
在top-k字符串相似性查询方面,除了第1部分介绍的文献[6],文献[7]通过动态调整q-gram的长度来解决 top-k字符串相似性查询,但是动态调整q-gram 长度非常费时,过滤代价很大,导致查询效率降低[6],且该方法需要为不同长度的q-gram建立索引,所需的存储空间大。文献[3]使用B树来索引S中字符串的特征(如q-gram),通过迭代方式遍历B树中的节点,动态计算节点下的字符串与σ的编辑距离下界,并基于此更新阈值进行过滤,最后通过计算编辑距离求得 top-k相似性结果。这种方法需要枚举很多字符串来动态更新阈值,尤其当k较小时,阈值不紧确,剪枝效果不好[6]。

图1 倒排索引
除以上工作外,和 top-k字符串相似性查询相关的工作还体现在基于阈值的字符串相似性查询和相似性连接。
基于阈值的字符串相似性查询的问题定义可表述为:给定字符串集合S、查询字符串σ、字符串相似性函数(如编辑距离)以及一个阈值τ,返回S中与σ相似性小于等于τ的字符串。
已有基于阈值的方法[1,2,4,5,7]在过滤阶段利用q-gram倒排表得到和查询串的公共q-gram不小于|σ|-q+1-qτ的候选字符串;验证阶段调用动态规划算法求解每个候选串和查询串的编辑距离,并根据阈值τ确定该候选是否满足条件。当应用该方法来求解top-k相似字符串时,由于很难根据k值确定合适的阈值τ,因而可能存在返回结果过多和过少的问题,进而导致根据不同的阈值重复计算、效率较低。
以上基于阈值的方法对查询串和被查询串使用的都是q-gram,称之为对称特征方案,与此相反,文献[10]研究基于非对称特征方案的字符串相似性查询问题(非对称特征方案指查询串用q-chunk,被查询串用q-gram,或者反过来也称为非对称特征方案),并给出了非对称特征方案下2个字符串相似的公共特征下界。即给定2个字符串s和σ,假设ed(s,σ) ≤τ,如下2个不等式成立。
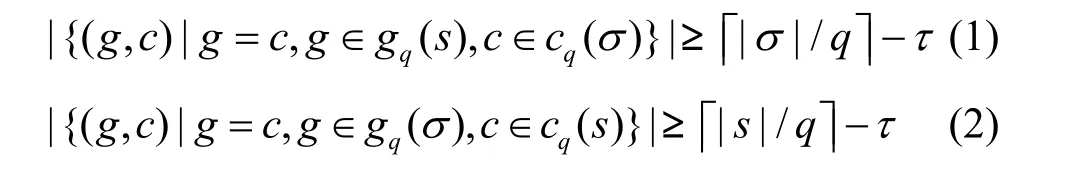
g和c表示相同的子串,对于式(1)和式(2)中二者匹配(即g=c),当且仅当g和c的位置差不大于τ。
相似性连接方面,对于给定的2个字符串集合S和R、字符串相似性函数(如编辑距离)以及相似性阈值,文献[8~10, 12~18]返回所有分属2个集合且相似性在阈值之内的(top-k)相似字符串对,感兴趣的读者可以参考相关文献获取详细信息。
3 top-k字符串相似查询算法
3.1 top-kLength算法
本节首先提出了一种长度跳跃索引,基于该索引提出了一种提前终止策略,根据该策略只需扫描局部倒排表;然后提出了查询字符串与字符串集合之间编辑距离的紧确下界,根据该下界,可以确定是否需要处理与查询串σ没有公共特征的字符串。基于上述2种策略,给出了基本的top-k字符串相似性查询算法,称为top-kLength 算法。
3.1.1 基于长度跳跃索引的长度过滤策略
给定查询串σ和字符串s,根据编辑距离的定义,如果 ed(σ,s)≤τ,则||s|-|σ||≤τ。根据该结论,将原始的q-gram倒排表(如图2(a)所示)按照字符串长度分段组织,如图2(b)所示,其中长度用来快速定位特定长度的字符串,在求解基于阈值的相似字符串时,通过该索引可以快速定位倒排表中和σ长度差不大于τ的字符串,从而实现基于长度的过滤策略,将该索引称为长度跳跃索引。

图2 长度跳跃索引举例
以图2(b)为例,倒排表中长度为9的字符串有s4和s5。
显然,基于长度跳跃索引可以高效支持基于阈值的相似字符串查询问题,但是当应用基于阈值的方法来解决 top-k相似字符串查询时,存在冗余计算问题。例如,给定查询串的长度|σ| = 9,k= 5,假设τ =1,则根据长度过滤的要求,需要处理的字符串长度应在[8,10]内,即s3,s4,s5,s7。由于被处理字符串个数小于5,需要增大阈值。当增大τ的取值来增加被处理字符串的个数时,需要重复计算s3,s4,s5,s7,显然存在重复计算问题。当|σ| = 9,k= 1,τ=1,假设ed(σ,s5) = 1,则不需要计算s3,s7,而基于阈值的方法会处理s3,s7,显然仍然存在冗余计算问题。
针对以上方法存在的冗余计算问题,提出一种基于长度跳跃索引的高效过滤策略,和以上方法相比,处理的字符串数量更少,且只需要一遍处理。其总体思路是根据被处理字符串和查询串的长度差从小到大进行处理。
定理1 假设当前top-k结果中与查询串σ编辑距离最大的字符串为sk,则对任意尚未处理的字符串r,如果||σ|-|r||≥ ed(σ,sk),则有 ed(σ,r)≥ ed(σ,sk)。
证明 假定 ed(σ,sk) =τk,因为||σ|-|r||≥τk,即σ和r的长度之差不小于τk,根据编辑距离的定义,必有 ed(σ,r)≥τk。证毕。
根据定理 1,当按照与查询串的长度差递增方式处理被查询串时,如果长度差满足定理1的条件,则可以提前终止,无需处理剩余字符串。
例2假定查询σ= “geometrics”,k= 1,以表1中的字符串集合为例,σ的q-chunk所对应的长度跳跃索引如图 3所示。因为|σ|=10,所以首先处理长度为10的字符串,即字符串s6,s7,此时ed(σ,s7) = 0;对于倒排表中剩余的任意字符串r有||σ|-|r||≥1,根据定理1,只需处理倒排表中的字符串s6,s7,其他字符串无需处理。
3.1.2 无匹配特征的字符串的处理策略

当处理完σ的q-chunk对应的倒排表后,根据定理2,假设当前top-k结果中与σ编辑距离最大的字符串为sk,当 ed(sk,σ)≤|cq(σ)时,可以保证当前top-k结果即最终结果;反之,当大于|cq(σ)|时,仅依赖σ对应的倒排表不能保证top-k结果的正确性,为了保证结果的正确性,这时仍然需要处理字符串集合中与查询串σ没有公共特征的字符串。
例3 假设σ=“geometric”,q= 2,k= 3,则|cq(σ)|=5。当处理完查询串σ的q-chunk对应的倒排表后,假设当前top-k结果与σ的编辑距离分别为0, 1, 2, 由于 2 < 5; 根据定理 2,当前 top-k结果即最终结果。假设当前top-k结果与σ的编辑距离分别为0, 1, 7,则仍需要处理字符串集合S中与σ没有公共特征的字符串,且这些字符串的长度应满足||s|-|σ||<ed(sk,σ)。
3.1.3 top-kLength算法描述
基于以上讨论,给出了top-kLength算法。在算法的执行过程中,使用一个优先队列Qtop-k来保存当前所求的 top-k结果,优先队列中的元素个数上限为k。
算法1top-kLength算法
输入:字符串集合S,查询字符串σ,结果个数k

图3 提前终止策略举例
输出:top-k相似字符串

算法1按照与查询字符串长度差递增的方式来处理倒排表中的字符串,初始化最初的长度差为ld=0(第2)行)。算法首先得到查询字符串σ的q-chunk对应的倒排表(第 3)行),在第 4)~10)行,根据长度差及长度跳跃索引确定满足||s|-|σ||=ld的局部倒排表(第5)行),然后调用 processPartialInvList()来计算局部的top-k结果(第6)行)。处理完局部的倒排表后,如果Qtop-k中有k个结果且head(Qtop-k).dis<ld+1 (第7)行),则根据定理1可以提前终止,不需要遍历剩余的倒排表;否则按照与查询字符串长度差递增的方式来处理剩余的倒排表。当处理完σ的q-chunk对应的倒排表后,算法得到当前的 top-k结果。最坏情况下,当 head(Qtop-k)dis> |cq(σ)|时,根据定理 2,仅依赖查询串对应的倒排表不能保证当前 top-k结果等于最终的结果。为了保证结果的正确性,这时仍然需要处理字符串集合中与查询串σ没有公共特征的字符串(第11)和12)行)。本文使用动态规划计算2个字符串的编辑距离[19]。
3.2 top-kLengthCount算法
与用基于阈值的方法来计算 top-k相似字符串相比,虽然 top-kLength 算法避免了对字符串的重复处理,且减少了需要处理的字符串数量,但对于需要处理的每个字符串,都需要计算编辑距离,代价较高。针对以上问题,提出了自适应计数过滤策略,进一步减少需要计算编辑距离的字符串数量。
3.2.1 自适应计数过滤策略
定理3 假设当前top-k结果中与查询串σ编辑距离最大的字符串为sk,ed(σ,sk) =τk,对于下一个要处理的字符串s,如果 ed(s,σ) ≤τk,则有下面的不等式(3)和式(4)成立

证明 首先证明式(3),式(4)根据对称性可得。
定理 3说明,下一个被处理的字符串是否能被过滤掉,依赖于当前所求得的sk与查询串σ的匹配特征个数。与文献[11]不同,对于top-k相似性查询,应用定理3时,阈值是动态调整的。在处理字符串的过程中,τk是单调递减的,所以公共特征匹配个数的下界在不断增大,因此可以过滤更多的字符串。
当应用定理3时,关键的操作是快速统计查询串的q-chunk与被查询串的q-gram的匹配个数。提出一种自适应的归并跳跃策略来求解查询串的q-chunk与被查询串的q-gram的匹配个数,如函数adaptiveMergeSkip所示。
假设当前top-k结果中与查询串σ编辑距离最大的字符串为sk,ed(σ,sk) =τk,则根据定理 3,后续处理的字符串和σ的匹配个数不能少于,函数adaptiveMergeSkip中用Tk表示该阈值。第2个输入参数INVp表示根据长度跳跃索引得到的对应特定长度的局部倒排表集合。
输入:INVp, 查询字符串σ,结果个数k,特征匹配阈值Tk
输出:top-k相似字符串


函数adaptiveMergeSkip使用优先队列Qp来存储当前需要处理的元素,Qp中元素按照id升序排序,并在第2)行将INVp中每个倒排表的第一个待处理元素插入Qp。在第3)~21)行,只要Qp不空,算法首先将与队头元素表示的字符串相同的所有元素出队列(第5)行),如果当前Qtop-k中少于k个结果,则算法直接计算队头元素所表示的字符串s和查询串的编辑距离,并将计算结果插入Qtop-k(第6)~8)行),并将弹出元素涉及的倒排表中的下一个元素入Qp(第 9)行)。反之,如果|Qtop-k| >k,算法首先计算下一个候选字符串s和σ的公共匹配个数的下界Tk(第11)行),然后判断出队列元素个数n和Tk的关系。如果n<Tk(第 12)行满足),则调用 pushBinSearch()(第 13)行),从队列中进一步弹出Tk-1-n个元素,加上前面处理的元素,总共从优先队列中出来Tk-1个元素。因为所有的倒排表中按照字符串id递增排序,令s’表示当前的队头元素,对于元素id小于s’的元素对应的字符串,其匹配的特征个数最好的情况下是Tk-1,必小于Tk,所以对于弹出元素的Tk-1个倒排表,直接定位到大于等于s’的最小元素r,中间的元素表示的字符串不需要处理,然后将r插入优先队列Qp。如果n≥Tk,则根据位置进一步计算n个元素中匹配的特征个数m(第15)行),如果m≥Tk,调用verifyEDThreshold( )函数计算s和σ的编辑距离d(第17)行),当d小于τk,即s和σ的编辑距离小于当前top-k结果和σ的最大编辑距离,则用s替换Qtop-k中编辑距离最大的字符串(第 18)~20)行)。并将弹出元素涉及倒排表中的下一个元素入Qp。
例 4假设经过长度过滤得到的局部倒排表如图4(a)的虚线框所示,且Tk=4。为了处理虚线框中的字符串,函数 adaptiveMergeSkip()首先将每个倒排表的第一个待处理元素,即36,100,50,115,115进入优先队列,如图4(b)所示。然后36出队列,这时n=1,由于1<Tk=4,所以再从优先队列中弹出Tk-1-n=2个元素,即弹出50和100,这时共有Tk-1=3个元素出队列,50和100不可能是满足条件的结果,可以直接跳过,无需计算编辑距离。之后当前优先队列中最小的元素为 115。对于刚刚弹出元素的Tk-1=3个倒排表,直接定位大于等于115的最小元素,这样可以跳过很多不可能成为top-k结果的元素,队列状态如图4(c)所示。下次处理时,当前优先队列的头元素为 115,个数为 4,调用基于阈值的编辑距离函数 verifyEDThreshold()来验证查询串σ和115对应的候选串的编辑距离。如果二者的编辑距离小于当前 top-k结果的最大编辑距离,则更新当前的 top-k结果,并根据定理 3更新匹配的q-gram和q-chunk的阈值为Tk。

图4 adaptiveMergeSkip函数举例
假设top-k结果中与查询串σ编辑距离第k大的字符串为sk, ed(σ,sk) =τk,在给定τk情况下只需判断字符串σ与s的编辑距离是否大于τk,根据文献[15]中的length pruning 策略,可以降低计算编辑距离的时间复杂度,如果2个字符串的编辑距离大于τk,则返回τk+1,否则返回实际编辑距离,用verifyEDThreshold(s1,s2,τk)表示基于阈值的编辑距离算法,verifyED(s1,s2)表示计算2个字符串的实际编辑距离的动态规划算法。
与 merge-skip[1]使用固定阈值的方法不同,adaptiveMergeSkip 函数的阈值是动态调整的。可以看出,首先使用长度跳跃索引定位特定长度的字符串,并使用 adaptiveMergeSkip函数对局部倒排表进行处理,可以首先定位与查询字符串较相似的字符串,所以τk可以快速降低,相应的q-gram和q-chunk的匹配个数快速增加,从而加速扫描查询相关的倒排表。
3.2.2 top-kLengthCount算法描述
基于以上介绍的自适应计数过滤策略,给出了top-kLengthCount算法,如算法2所示。
算法2top-kLengthCount 算法
输入:字符串集合S,查询字符串σ,结果个数k
输出:top-k相似字符串

top-kLengthCount算法与top-kLength算法的不同之处体现在:1)在第6)行调用adaptiveMergeSkip函数对局部倒排表进行处理,并在处理完局部倒排表后,根据定理2 更新Tk(第 10)行);2)与 top-kLength算法处理字符串集合中与查询串σ没有公共特征的字符串不同,在processNoCommonStr()中,虽然σ的q-chunk集合与未处理的字符串的q-gram集合的交集为空,根据式(4),通过计算σ的q-gram集合与未处理的字符串的q-chunk集合的交集(第3)行),进一步减少需要计算编辑距离的字符串。如果匹配的特征个数大于下界(第 4)行),则调用verifyEDThreshold()进行编辑距离的计算(第5)行),如果二者的编辑距离小于当前 top-k结果的最大编辑距离,则更新当前的top-k结果(第6)~8)行)。
4 实验评估
4.1 实验环境
实验所用的机器配置为Intel Pentium G2020,2.90 GHz CPU,4 GB内存,操作系统为 Ubuntu 12.04 LTS。
根据文献[6]的实验结果,Range算法比AQ[3]、Bed-tree[4]和 Flamingo[1]更高效,因此实验中只和Range算法进行比较,Range算法源码由原文作者提供注1注1 http://dbgroup.cs.tsinghua.edu.cn/dd/projects/topksearch/index.html注2 http://dbgroup.cs.tsinghua.edu.cn/dd/data/data.tar注3 http://www.ncbi.nlm.nih.gov/pubmed/注4 http://www.cse.unsw.edu.au/~weiw/project/simjoin.html#_download。基于C++实现了本文中提出的算法,并使用-O3flag的GCC4.8.2进行编译。实验环境与Range算法完全相同。
所用数据来自3个真实数据集,分别是:1) word数据集注2注1 http://dbgroup.cs.tsinghua.edu.cn/dd/projects/topksearch/index.html注2 http://dbgroup.cs.tsinghua.edu.cn/dd/data/data.tar注3 http://www.ncbi.nlm.nih.gov/pubmed/注4 http://www.cse.unsw.edu.au/~weiw/project/simjoin.html#_download,包含常用的英语单词字符串;2) author数据集,包含作者名称的字符串,从期刊pubMed注3注1 http://dbgroup.cs.tsinghua.edu.cn/dd/projects/topksearch/index.html注2 http://dbgroup.cs.tsinghua.edu.cn/dd/data/data.tar注3 http://www.ncbi.nlm.nih.gov/pubmed/注4 http://www.cse.unsw.edu.au/~weiw/project/simjoin.html#_download提取;3) DBLP数据集注4注1 http://dbgroup.cs.tsinghua.edu.cn/dd/projects/topksearch/index.html注2 http://dbgroup.cs.tsinghua.edu.cn/dd/data/data.tar注3 http://www.ncbi.nlm.nih.gov/pubmed/注4 http://www.cse.unsw.edu.au/~weiw/project/simjoin.html#_download,包含作者名字与文章名字连接起来的长字符串。表2给出了3个数据集的基本统计信息。图5中展示了3个数据集中字符串的长度分布情况。由图5可知,所有数据集的字符串长度都呈近似的正态分布,其中word和author数据集的字符串长度较短,而DBLP数据集的字符串长度较长。
对于每一个数据集,从数据集中随机选择了100组查询,然后比较平均运行时间。

表2 数据集基本信息
4.2 性能比较
4.2.1q-gram长度的确定
由于本文算法的性能与q-gram的长度相关,这部分首先通过实验为每个数据集确定合适的q-gram长度。在每个数据集上运行100个查询,每个查询返回top-100结果。图6展示了在q-gram长度变化的情况下,本文算法的性能波动情况。由图6可知,本文算法在word/author/DBLP数据集上性能最好时q-gram的长度分别为2、2、6,因此,在后续实验中,本文算法的运行时间都是基于这里确定的q-gram长度。

图5 数据集字符串长度分布

图6 不同q-gram 长度运行时间
4.2.2 过滤效果比较
由于本文得到的Range算法是二进制可执行代码,没有算法运行过程中的统计信息,因此这里的过滤效果仅展示本文方法之间的比较。
由表3可知,通过长度跳跃索引进行过滤,在求解top-10结果时,本文算法无需计算所有字符串(每个数据集的字符串数量见表2)的编辑距离。对于word、author、DBLP数据集来说,需要计算编辑距离的字符串数量分别为22 488、279 046、976(表3第5列),比例分别为相应数据集中字符串总量的3/20, 1/5, 1/100。进而,通过提出的自适应计数过滤技术,在验证结果时计算编辑距离的字符串数量分别为9 266、134 560、141,和不使用计数过滤技术相比,需要计算编辑距离的字符串数量分别为原来的2/5, 12/25, 7/50。
另外,从表3的第3列可知,算法top-kLength Count需要的过滤时间比算法top-kLength稍长,但是验证阶段所用时间得到了显著的改善(表3第4列),原因在于通过计数过滤,减少了需要计算编辑距离的字符串数量(表3第5列)。
4.2.3 查询时间比较
图 7给出本文的算法 top-kLengthCount和Range算法的运行时间比较。由图 7(a)可知,对于word数据集而言,算法top-kLengthCount在k小于18的时候要比Range算法慢,但是随着k值的增大本文的算法要比 Range算法更高效。原因在于Range算法采用一种递进的方式来计算top-k结果,需要计算所有字符串的前缀,当k值较小的时候,需要计算的字符串前缀的数量少,运行时间比较短;但随着k值逐步增大,需要计算前缀字符串数量迅速增多(根据文献[6],当k从10变到100时,需要处理的字符串前缀数量增长了 5倍多),需要的运行时间相应变长,而本文的算法 top-kLengthCount按照与查询串长度差递增的方式访问倒排表中的字符串,同时使用计数过滤并结合提前终止条件来减少需要处理的字符串,当k值增大时,需要处理的字符串数量的增长没有Range算法增长的字符串前缀数量(当k从10变到100时,需要处理的字符串前缀数量增长了3倍),因而当k值增大时,可以获得比Range算法更好的处理性能。

表3 3个数据集上处理top-10结果时本文算法的性能比较

图7 top-kLengthCount算法与Range算法性能对比
随着字符串数量和平均长度的同时增长,本文的算法top-kLengthCount在author和DBLP数据集上较 Range算法的优势更明显(如图 7(b)和图 7(c)所示)。原因在于,字符串数量以及字符串长度同时增加(word数据集包含146 033个字符串,而author和DBLP数据集分别包含1 266 150和156 506个字符串,长度由8.76增长到151.9)会导致字符串前缀数量的成倍增加,加之相应的查询串变长,Range需要处理的字符串前缀数量的增长速度更快,所需时间更长。与之对应,本文算法基于自适应的长度和计数过滤,可以过滤很多字符串而不用处理。由图7(b)和图7(c)可知,当k取100时,本文的算法在author数据集上比Range 算法快4.5倍,在DBLP数据集上比Range算法快2.5倍。
4.3 扩展性
图8展示的是本文算法top-kLengthCount在不同k值和不同大小的数据集上处理100个查询的平均运行时间。

图8 可扩展性
由图8可知,随着数据集和k值的增大,算法top-kLengthCount体现出了较好的扩展性。以author数据集为例,当k=100、字符串个数是900 000时,运行时间是326 ms,当数据集是1 200 000个字符串时,运行时间是390 ms。在DBLP数据集上,当k=10时,基于150 000字符串的运行时间比基于120 000和90 000个字符串的运行时间还要少,原因在于算法top-kLengthCount按照与查询字符串的长度差递增的方式访问倒排表,随着数据集的增大,在局部倒排表中有更多的相似字符串。按照早终止策略,可以更早地得到 top-k结果,所以在数据集增大的时候,运行时间会更短。
5 结束语
针对已有 top-k相似字符串算法存在的冗余计算问题,提出了基于长度跳跃索引的2种高效的自适应过滤策略,包括基于字符串长度差递增方式的过滤策略和基于当前 top-k结果的动态计数过滤策略,以减少字符串之间的编辑距离计算次数,针对查询串对应的倒排表存在不能正确求解 top-k结果的问题,提出了查询字符串与不匹配字符串集合的编辑距离下界来进一步减少字符串之间编辑距离的计算次数。实验结果表明,被处理的字符串越长,本文方法的优势越明显;k=100时,所提算法比现有的最好算法快2~4倍。
[1] LI C, LU J, LU Y. Efficient merging and filtering algorithms for approximate string queries[A]. ICDE[C]. 2008. 257-266.
[2] KAHVECI T, SINGH A K. Efficient index structures for string databases[A]. VLDB[C]. 2001.351-360.
[3] ZHANG Z, HADJIELEFTHERIOU M, OOI B C,et al. Bed-tree: an all-purpose index structure for string similarity query based on edit distance[A]. SIGMOD[C]. 2010.915-926.
[4] CHAUDHURI S, GANJAM K, GANTI V,et al. Robust and efficient fuzzy match for online data cleaning[A]. SIGMOD[C]. 2003.313-324.
[5] HADJIELEFTHERIOU M, KOUDAS N, SRIVASTAVA D. Incremental maintenance of length normalized indexes for approximate string matching[A]. SIGMOD[C]. 2009.429-440.
[6] LI G, DENG D, FENG J,et al. Top-kString Similarity Search with Edit-Distance Constraints[A]. ICDE[C]. 2013.925-936.
[7] YANG Z, YU J, KITSUREGAWA M. Fast algorithms for top-kapproximate string matching[A]. AAAI[C]. 2010.1467-1463.
[8] GRAVANO L, IPEIROTIS P G, JAGADISH H V,et al. Approximate string joins in a database (almost) for free[A]. VLDB[C]. 2001. 491-500.
[9] XIAO C, WANG W, LIN X. Ed-join: an efficient algorithm for similarity joins with edit distance constraints[A]. VLDB[C]. 2008.933-944.
[10] XIAO C, WANG W, LIN X,et al. Top-kset similarity joins[A].ICDE[C]. 2009.916-927.
[11] QIN J, WANG W, LU Y,et al. Efficient exact edit similarity query processing with the asymmetric signature scheme[A]. SIGMOD[C].2011.1033-1044.
[12] ARASU A, GANTI V, KAUSHIK R. Efficient exact set-similarity joins[A]. VLDB[C]. 2006. 918-929
[13] CHAUDHURI S, GANTI V, KAUSHIK R. A primitive operator for similarity joins in data cleaning[A]. ICDE[C]. 2006.5-16.
[14] SARAWAGI S, KIRPAL A. Efficient set joins on similarity predicates[A]. SIGMOD[C]. 2004.743-754.
[15] BAYARDO R J, MA Y, SRIKANT R. Scaling up all pairs similarity query[A]. WWW[C]. 2007.131-140
[16] WANG J, LI G, FENG J. Trie-join: efficient trie-based string similarity joins with edit-distance constraints[A]. VLDB[C]. 2010. 1219-1230.
[17] WANG J, LI G, FENG J. Fast-join: An efficient method for fuzzy token matching based string similarity join[A]. ICDE[C]. 2011.458-469.
[18] LI G, DENG D, WANG J,et al. Pass-join: A partition-based method for similarity joins[A]. VLDB[C]. 2011.253-264.
[19] WAGNER R A, ANDFISCHER M J. The string-to-string correction problem[A]. ACM[C]. 1974.168-173.
