(2+1)-维强排斥玻色-爱因斯坦凝聚体中的解析解*
2013-10-25姜云青
姜云青, 林 机
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
(2+1)-维强排斥玻色-爱因斯坦凝聚体中的解析解*
姜云青, 林 机
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
运用经典李群方法,以“硬核”玻色子为模型,研究了原子间为强排斥作用的(2+1)维玻色-爱因斯坦凝聚体中的物质波.在特殊情况下,得到了物质波的一些解析解,包括暗孤子解、亮孤子解及周期解.分析了此强关联体系的物理参量,包括最近邻格点间的跃迁强度、最近邻格点间原子的相互作用,对物质波的波速及振幅的影响.
经典李群方法;“硬核”玻色子;玻色-爱因斯坦凝聚;解析解
0 引 言
物质波的非线性动力学已成为当今物理学的研究热点之一.近年来,稀薄金属气体中玻色-爱因斯坦凝聚(简称BEC)的实现为非线性物理学的研究开创了新领域.在BEC中,物质波暗孤子是凝聚体密度缺损的一种表现,只存在于凝聚体的内部,而物质波亮孤子本身就是凝聚体,且不同性质的原子间相互作用会形成不同的物质波孤子.对于原子间相互作用比较弱的情形,BEC的动力学问题可由Gross-Pitaevskii(GP)方程[1]来描述:当相互作用为排斥作用时,GP方程有暗孤子解[1];当相互作用为吸引作用时,GP方程有亮孤子解[2];二维情况下有模拟的孤子解[3]. 实验上弱相互作用BEC中的暗孤子[4]、亮孤子[5]等也已被成功观察.对于凝聚原子相互作用比较强的情形,当原子之间为强排斥作用时,玻色体系的行为就如同相互排斥的粒子体系,“硬核”玻色子(hard-core boson (HCB))就能恰如其分地表现这一点,并在此基础上建立了“硬核”(Bose-Hubbard)模型.一维“硬核”玻色气体也称为“Tonks-Girardeau”原子气[6-7],于2004年在实验上实现了这一物质状态[8].
对于强排斥BEC体系,不再用GP方程对其动力学行为进行描述[9-10],非“GP”型孤子是近期研究的热点[11].对于“硬核”玻色子体系,一维情形下的暗孤子[12]、亮孤子[13]及其他类型的孤子[14]已被获得,但现有的数值及解析结果并不多,特别对于高维体系,解析结果更是少.2009年,Balakrishnan等[15]用新的“自旋相干态平均法(spin-coherent state averages)”得出了一维强排斥BEC的新型孤子解[14]. 本文在此工作的基础上,运用经典李群方法[16]研究了(2+1)维的情形,得出了(2+1)维强排斥BEC中物质波的一系列解析结果.
1 经典李群约化
以近邻格点原子间存在相互作用的“硬核”Bose-Hubbard为模型,(2+1)维强排斥BEC体的动力学方程为[14]
式(1)中:下标表示对时间变量t和空间变量x,y的求导;η(r),δ(r)分别表示BEC中凝聚原子的局域序参量(local order parameter)和粒子-空穴不平衡变量(particle-hole imbalance variable);Ue=2(T-V);Ve=Va2;T为Bose-Hubbard模型中最近邻格点间粒子的跃迁强度;V为引入的最近邻格点上原子间的相互吸引作用(V>0)(当V<0,即为排斥作用时,所得结果也成立);a为晶格常数;μ为化学势.由“自旋相干态平均法”[16]得凝聚序参数η(r)=2-1sin(θ)ejφ(r);凝聚粒子数密度ρc=|η|2=4-1sin2(θ);总粒子数密度ρ=sin2(θ/2).这里易得ρc=ρ(1-ρ),而对于描述弱相互作用的BEC的GP方程,有ρc=ρ.又总粒子数密度ρ与空穴数密度ρh有关系ρh=1-ρ,所以,可得粒子-空穴不平衡变量δ(r)=ρh-ρ=1-2ρ=cos(θ(r)).将η(r),δ(r)代入式(1)中,消去η,得到关于δ,φ的方程组
式(2)中取ћ=1,m=1.
对方程组(2),运用经典李群方法,要求方程组(2)的解集在无穷小变换{x,y,t,δ,φ}→{x,y,t,δ,φ}+ε{X,Y,T,ξ,ζ}是不变的,就要求下述方程

成立.式(3)中的Pr(2)V是保持方程组(2)不变的单参数群的向量场(生成元)V=X∂x+Y∂y+T∂t+ξ∂δ+ζ∂φ的二阶延拓
式(4)中系数Kt=∂i(K-Xkx-Tkt)+Xkxi+Tkit,Kii=∂ii(K-Xkx-Tkt)+Xkxii+Tkiit(K=(ξ,ζ),k=(δ,φ),i=(x,y,t))分别表示一阶无穷小和二阶无穷小.把式(2)、式(4)代入方程(3),将含有δ,φ的各阶导数合并同类项,使δ,φ各阶导数的系数为零,即可得到一系列线性偏微分方程组,解之,可以得到

式(5)中,a1,c1,c2,c3,c4是任意实常数.当a1=0时,通过积分特征方程
可以得到相似变量z和相似解δ,φ为

式(7)中,f(z),g(z)为积分不变量且c1=c2.将式(7)代入方程组(2),通过E1对z积分得

c是积分常数.再将式(8)代入E2,则可得约化方程
式(9)中,g′,f′,f″分别表示对变量z的一次、二次求导.方程(9)为非线性常微分方程,对其求解,再联合式(7)、式(8),则可得到方程(2)关于δ,φ的解.再由上文已知δ(r)=1-2ρ,ρc=ρ(1-ρ),则可得(2+1)维具有强排斥BEC中物质波ρc的解析解形式.
2 精确解
方程(9)是一个复杂的非线性常微分方程,直接求解非常困难.但是,当方程的参数取某些特定值的情况下,方程(9)存在着一系列解析解.以下给出一系列关于物质波ρc的精确解析解形式,主要有暗孤子、亮孤子及周期解形式.
2.1暗孤子

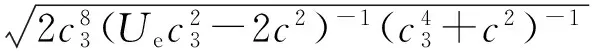

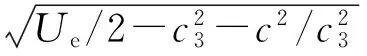

图1 物质波暗孤子在t=1时刻的演化图 图2 物质波暗孤子随速度变化图
2.2亮孤子
情形1



图3 物质波亮孤子在t=1时刻的演化图
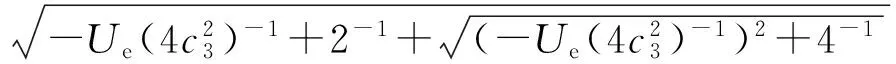

(13)
v=c1/c3为孤子的传播速度,只与参量Ue有关.该物质波为一亮孤子,图3即为t=1时物质波亮孤子的演化图,具体参数取值为c3=c1=c=1,v=1,b1=0.5.
情形2


则凝聚的粒子数密度为

它是一定态的亮孤子解,如图4所示,取c3=1.此特殊情形中,有Ue=2(T-V)<0,即要求最近邻格点间的跃迁强度T小于最近邻格点上原子间的相互作用V.因此可以得出,当体系中的物理参量μ与T,V取适当的关系时,此凝聚体中的物质波为一定态亮孤子波,此时,强关联体系的物理量T或V的变化不会引起物质波的变化,即对凝聚体中粒子的空间分布几率无影响.
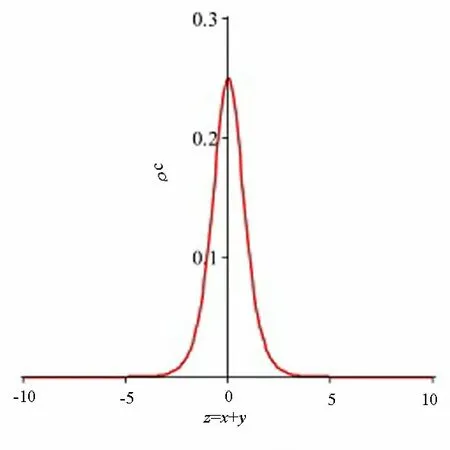
图4 物质波定态亮孤子的演化图 图5 物质波定态hump孤子的演化图
情形3
当Ue=0,c4=(μ∓c23)c3,Ve=1,c=0,c1=0时,方程(9)有解

强关联BEC中的凝聚粒子数密度为

它是一定态的hump孤子,如图5所示,取参量c3=1.在此情形中,特别是当Ue=2(T-V)=0,即要求最近邻格点上的跃迁强度T等于最近邻格点上原子间的相互作用V,并且化学势μ独立存在,与变量Ue无关.同上,在此情形中,强关联体系的物理参量T或V的变化不会影响此hump孤子的宽度及振幅,即不会影响凝聚体中粒子的空间分布几率.
2.3周期解
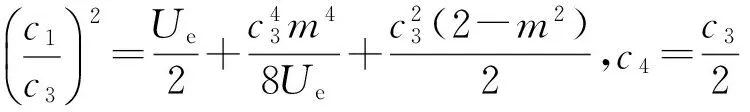

图6 周期性物质波的演化图
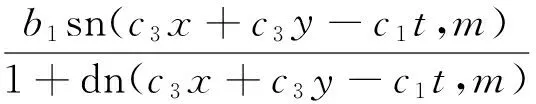
(18)



3 结 论
本文以“硬核”玻色气体为模型,研究了原子间为强排斥作用的(2+1)维玻色-爱因斯坦凝聚体中的物质波.首先,由具有强排斥作用的玻色-爱因斯坦凝聚体的动力学方程出发,运用经典李群方法,通过约化,得到了一常微分方程,求解此常微分方程,最终得到了物质波的一系列解析解,包括亮孤子、暗孤子与周期解.然后,对这些解的物理意义进行了讨论,分析了各种情况下所得的物质波中,强关联体系中的物理参量如最近邻格点间粒子的跃迁强度、最近邻格点上原子间的相互作用对物质波的传播速度及振幅的影响.
[1]Pitaevskii L,Stringari S.Bose-Einstein condensation[M].Oxford:Oxford University Press,2003.
[2]Al Khawaja U,Stoof H T C,Hulet R G,et al.Bright soliton trains of trapped Bose-Einstein condensate[J].Phys Rev Lett,2002,89(20):200404-200408.
[3]Lashkin V M.Two-dimensional nonlocal vortices,multipole solitons,and rotating multisolitons in dipolar Bose-Einstein condensates[J].Phys Rev A,2007,75(4):43607-43613.
[4]Burger S,Bongs K,Dettmer S,et al.Dark solitons in Bose-Einstein condensates[J].Phys Rev Lett,1999,83(25):5198-5201.
[5]Strecker K E,Partridge G B,Truscott A G,et al.Formation and propagation of matter-wave soliton trains[J].Nature,2002,417:150-153.
[6]Girardeau J M.Relationship between systems of impenetrable bosons and fermions in one dimension[J].J Math Phys,1960,1(6):516-524.
[7]Lieb E H,Liniger W.Exact analysis of an interacting Bose gas. I . The general solution and the ground state[J].Phys Rev,1963,130(4):1605-1616.
[8]Kinoshita T,Wenger T,Weiss D S.Observation of a one-dimensional Tonks-Girardeau gas[J].Science,2004,305(5687):1125-1128.
[9]Kolomeisky E B,Newman T J,Straley J P,et al.Low-Dimensional bose liquids:beyond the Gross-Pitaevskii approximation[J].Phys Rev Lett,2000,85(6):1146-1149.
[10]Mishmash R V,Danshita I,Clark C W,et al.Quantum many-body dynamics of dark solitons in optical lattices[J].Phys Rev A,2009,80(5):053612-053625.
[11]Krutitsky K V,Larson J,Lewenstein M.Dark solitons near the Mott-insulator-superfluid phase transition[J].Phys Rev A,2010,82(3):033618-033627.
[12]Girardeau M D,Wright E M.Dark solitons in a one-dimensional condensate of hard core bosons[J].Phys Rev Lett,2000,84(25):5691-5694.
[13]Gligoric G,Maluckov A,Hadzievski L,et al.Bright solitons in the one-dimensional discrete Gross-Pitaevskii equation with dipole-dipole interactions[J].Phys Rev A,2008,78(6):063615-063625.
[14]Balakrishnan R,Satija I I,Clark C W.Particle-Hole asymmetry and brightening of solitons in a strongly repulsive Bose-Einstein condensate[J].Phys Rev Lett,2009,103(23):230403-230407.
[15]Balakrishnan R,Sridhar R,Vasudevan R.Hydrodynamics of superfluid He4in a pseudospin model[J].Phys Rev B,1989,39(1):174-182.
[16]Lakshmannan M,Kaliappan P.Lie transformations,nonlinear evolution equations,and Painlevé forms[J].J Math Phys,1983,24(4):795-807.
(责任编辑 杜利民)
Analyticalsolutionsofthe(2+1)-dimensionalstronglyrepulsiveBose-Einsteincondensate
JIANG Yunqing, LIN Ji
(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)
Using the classical Lie-group method, it was studied a (2+1)-dimensional strongly repulsive Bose-Einstein condensate system known as the hard-core bosons and some analytical solutions were obtained including dark soliton, bright soliton and periodic solutions for the matter wave of the strongly repulsive Bose-Einstein condensate in special cases. It was also elucidated how the factors including the nearest-neighbor hopping parameter and the nearest-neighbor interaction of the system to determine the solution characteristics including the velocities and the amplitudes of the matter waves.
classical Lie-group method; hard-core bosons; Bose-Einstein condensates; analytical solutions
O41
A
1001-5051(2013)02-0182-06
2012-03-08
国家自然科学基金资助项目(11175158)
姜云青(1984-),女,江苏淮安人,硕士研究生.研究方向:非线性物理.
林 机.E-mail: linji@zjnu.cn.
