扶手椅型石墨烯纳米带在单轴应力下的能隙调控*

孙 娜, 童国平

(浙江师范大学 凝聚态物理研究所,浙江 金华 321004)

扶手椅型石墨烯纳米带在单轴应力下的能隙调控*

孙 娜, 童国平

(浙江师范大学 凝聚态物理研究所,浙江 金华 321004)

利用紧束缚方法研究了扶手椅型石墨烯纳米带沿其长度方向受单轴应力的电子能谱及能隙与形变量的关系.结果表明：在一定的应力下，3m和3m+1型纳米带的能隙随纳米带宽度的变化呈现零能隙拐点，而这种拐点随着非近邻项的逐渐计入向着纳米带宽度窄的方向移动.当带宽较窄时，无论非近邻项是否计入，除了3m+2外,只有3m的三近邻情形能隙与形变量(小形变)的曲线才有拐点；随着宽度的增加，除了3m+1的最近邻情况外，3种宽度3m，3m+1和3m+2都出现零能隙拐点.

石墨烯纳米带；紧束缚方法；单轴应力；能隙

0 引 言

自从2004年由Novoselov等[1]制备出石墨烯以来，人们对其拓朴结构产生了极大的研究兴趣.通过研究发现，不同的几何结构有不同的电子性质及其输运性质.由于石墨烯有极好的电子迁移率，因而在单电子晶体管、纳米聚合物等电子器件方面将有很好的应用前景.由于石墨烯纳米带(GNRs)是几何结构受限的石墨烯，依据边界形状的不同，常见的石墨烯纳米带可分为扶手椅型(armchair)和锯齿型(zigzag).石墨烯纳米带的准一维特征及可以调节带隙的性质，在纳米电子器件运用中有着重要的意义.理论上研究石墨烯纳米带的电子性质，其方法主要有基于第一性原理的密度泛函理论[2]、狄拉克理论[3]、紧束缚近似[4-7]等.由紧束缚方法研究表明，锯齿型石墨烯纳米带是金属性的[6]，而扶手椅型石墨烯纳米带的金属性和绝缘性与宽度有关；电子的非近邻跳跃对GNRs的能带及能隙的影响也是明显的[8-9].另外，当GNRs的几何形状确定后，如何调节其电子性质也成为人们关注的热点.由于石墨烯有非常好的强度，故可利用施加外力[9]或单轴应力[10-12]来改变其电子性质.运用ab initio或第一性原理方法来计算电子性质,其结果比较准确，且无需设定参数，但是现在用的计算软件使得计算的原子数是受限的.笔者将运用紧束缚近似、弹性力学理论及哈里森理论[13]来研究扶手椅型GNRs在单轴应力下的电子能谱和能隙随形变参数的变化特点，计算时分别考虑最近邻、次近邻和三近邻这3种情况，并且忽略了不同原子之间波函数的交叠.

1 理论与方法

石墨烯纳米带的电子性质主要是由π电子决定的，计及三近邻时石墨烯的紧束缚哈密顿量为

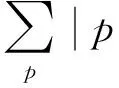
式(1)中:p〉和〈q|分别表示处于第p个和第q个碳原子的π电子态；求和指标(p,q),((p,q))和(((p,q)))分别表示对最近邻、次近邻和三近邻求和；ε0表示格点原子的自由能，这一项可吸收到H中，即取ε0=0；γ0,γ1和γ2分别表示最近邻、次近邻和三近邻跳跃积分，它们的值可取为[7]γ0=2.97 eV，γ1=0.076 eV,γ2=0.33 eV.由于每个元胞有2个不等价的原子，故波函数为

式(2)中:CA和CB是组合系数，将式(2)代入薛定谔方程HΨ〉=EΨ〉,可得GNRs的久期方程

忽略不同原子间的交叠积分(SAB=0),可解得

式(4)中,“+”表示导带，“-”表示价带.

图1 扶手椅型石墨烯纳米带(虚线框为晶胞)

扶手椅型石墨烯纳米带由2种子晶格A和B组成，其几何结构如图1所示，灰点表示A原子，黑点表示B原子.在y方向对碳原子依次从0到n+1标记，即n可以表示带的宽度.由于x方向上是无限长的，故仍有周期性.图1中的虚线框内是在x方向上的一个晶胞，含有2n个A原子和B原子，碳-碳键长a=0.142 nm.根据平移不变性，可选取沿x方向为平面波基矢.在紧束缚近似下，扶手椅型石墨烯纳米带(AGNRs)2个子晶格的波函数可写成

式(5)中：kx的取值仅局限于第一布里渊区；Nx表示x方向的元胞数；φA(i)和φB(i)分别是子晶格A和B的基波函数在y方向上的分量；NA和NB是归一化系数.A〉,B〉分别表示子晶格A和B的π电子波函数.由于纳米带的宽度有限，故其边界条件为

式(7)表明，y方向的波矢是量子化的.当n=6时，p=1表示驻波波长最长，即反映能带的宽度；而p=5代表着导带与价带之间的能隙.

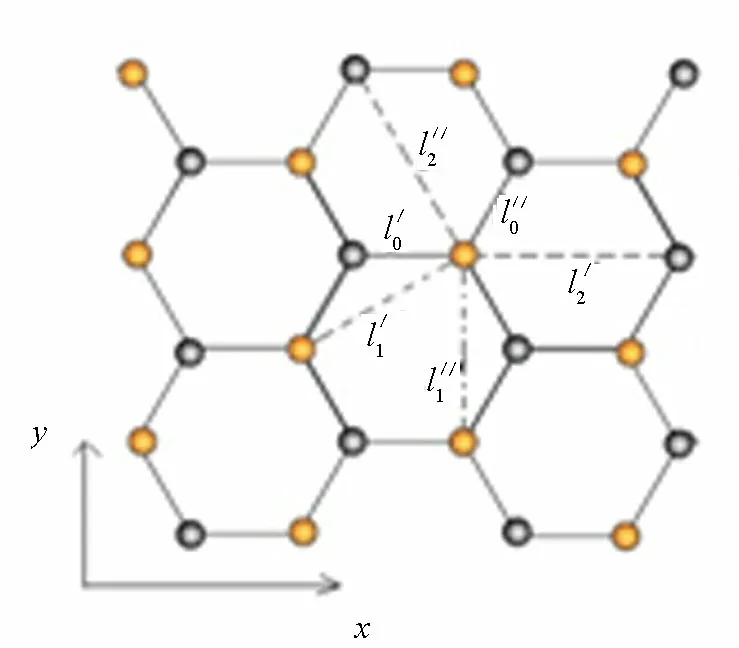
图2 沿x轴拉伸的石墨烯纳米带

设沿着x方向施加单轴应力[14-15]，AGNRs的形变如图2所示.根据弹性力学原理，如果形变较小，碳原子形变前的位置(R)与形变后的位置(R′)满足下列关系：

式(8)中,δ是沿x方向的应变系数.形变后碳-碳原子之间的键长发生改变，从而导致跳跃积分改变.根据Harrison公式[13]，跳跃积分和键长变化关系是γ′=(l′/l)2γ，这里l,l′分别表示形变前后碳-碳原子的键长，γ,γ′分别代表相应的跳跃积分.设形变后碳-碳原子间的最近邻距离为l′0,l″0，次近邻为l′1,l″1，三近邻为l′2,l″2，所对应的跳跃积分分别是γ′0,γ″0,γ′1,γ″1,γ′2,γ″2.

考虑最近邻时，形变后的跳跃积分为

由式(4)可得电子能谱为

考虑到次近邻时，电子的跳跃积分为

考虑到第三近邻时，电子的跳跃积分为

其电子能谱为

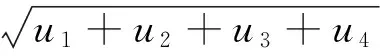
式(14)中:

2 计算结果与讨论

AGNRs的宽度可分为3种类型：n=3m;n=3m+1;n=3m+2(m是整数)，而n=3m+2是金属性的.当单轴应力沿着带的长度方向作用时， AGNRs的能带和能隙随之而改变.

下面分别就最近邻、次近邻和三近邻的情况进行计算和讨论.用ΔE′1,ΔE′2和ΔE′3分别表示最近邻、次近邻和三近邻的能隙变化，即

式(17)中:

当n一定时，纳米带的能谱与δ有关.考虑次近邻时n分别取6，7,8，δ分别取-10%，0，10%的能谱如图3所示.从图3可以看出，宽度一定时，拉伸或压缩会改变扶手椅型石墨烯纳米带的带隙.当n=6时，压缩能够明显地减小带隙，而拉伸能较大地增大带隙；当n=7时，情况恰好与n=6相反，但不如n=6那么显著；当n=8时，拉伸或压缩均使得金属型转变成非金属型.从图3中还可以看出，当n=7时出现1条水平导带和价带，即表现范霍夫奇异性，压缩使得2条能带间隔增大，而拉伸情况正好相反.在计算中发现，如果计及三近邻，范霍夫奇异性不再出现.

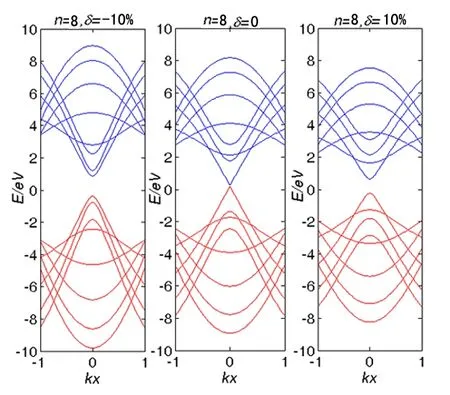
图3 考虑次近邻时 n=6,7,8在不同形变参数下的能谱

当δ一定时，能隙是宽度n的函数.为了弄清能隙的非近邻效应，图4给出了分别计及最近邻、次近邻、三近邻时，3种类型扶手椅型石墨烯纳米带能隙随宽度(用m表示宽度n)的变化.由图4不难看出，对于n=3m来说，当δ=-10%时能隙随着带宽的增加先减少到零再增加并且趋于稳定值,能隙变化存在拐点(零能隙)；当δ=0和δ=10%时能隙随宽度增加而减小.当n=3m+1时，δ=10%的能隙随带宽先减小到零再慢慢增加最后趋于固定值，也存在能隙的拐点；δ=0和δ=-10%时能隙减小，无拐点.当n=3m+2时，能隙不随带宽改变,是一个定值.比较图4还可以看出，对于n=3m纳米带压缩而言，随着非近邻的计入，能隙拐点向着小宽度方向移动.

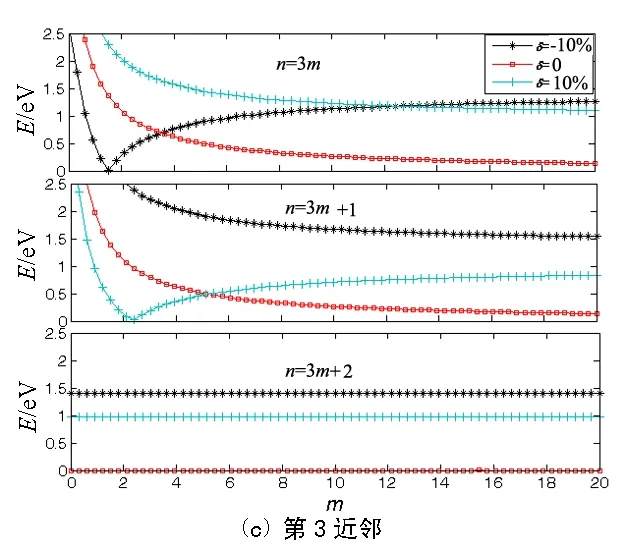
图4 形变一定时，3种不同类型的扶手椅型石墨烯纳米带的能隙随宽度的变化

图5 当n=6，7，8，18，19，20时能隙随形变参数的改变

当宽度n一定时，能隙随形变参数δ(-10%～10%)的变化如图5所示.在同一形变参数范围内，不同宽度的能隙变化不完全相同.n=6只有三近邻计入时才出现能隙变化的拐点;而n=8无论是最近邻还是三近邻情况，都有能隙的拐点出现，且拐点是重合的；当宽度n较大时，无论3m，3m+1还是3m+2型，最近邻与非最近邻几乎都会出现能隙变化的拐点.这些结果与第一性原理的结果[8]基本一致，用紧束方法来讨论可以作为结果的一种补充.从图5可见，“V”字形的出现意味着对于较宽的纳米带，在拐点附近调控能隙变得不易控制.

3 结 论

当石墨烯纳米带沿其长度方向受力应变时，紧束缚近似的计算结果显示：当形变一定时，3m和3m+1型纳米带的能隙随纳米带宽度的变化呈现零能隙拐点，而这种拐点随着非近邻项的逐渐计入向着小宽度带的方向移动；当带宽较窄时，无论是否考虑非近邻项，除了3m+2外能隙与形变量的曲线几乎没有拐点，但随着宽度的增加，3种宽度(3m，3m+1和3m+2)几乎都出现零能隙拐点.这些结果意味着，纳米带受力形变能够较大地改变其电子性质，而且非近邻项是否被考虑，对计算结果也非常重要.值得一提的是，笔者的结果呈现出长带特点，即在长度方向具有周期性，从上面的计算与分析可知，在长度方向通过拉伸或压缩石墨纳米带是完全可以调控其能隙的，这对纳米带电子器件的制作有重要参考作用.

[1]Novoselov K S,Geim A K,Morozov S V,et al.Electric fied effect in atomically thin carbon films[J].Science,2004,306(5696):666-669.

[2]Son Y W,Cohen Marin L,Louie S G.Energy gaps in graphene Nanoribbons[J].Phys Rev Lett, 2004,97(21):216803.

[3]Brey L,Ferting H A.Electronic states of graphene nanoribbons studied with the Dirac equation[J].Phys Rev B,2006,73(23):235411.

[4]Zheng Huaixiu,Wamg Zhengfei,Luo Tao.Analytical study of electronic structure in armchair graphene nanoribbons[J].Phys Rev B,2007,75(16):165414.

[5]Son Y W,Cohen M L,Louie S G.Halfk-metallic graphene nanoribbons[J].Nature,2006,444(7117):347-349.

[6]Areshkin D,Gunlycke D,White C T.Graphene nanostrip digital memory device[J].Nano Lett,2007,7(12):3608-3611.

[7]Reich S,Maultzsch J,Thomsen C.Tight-binding description of graphene[J].Phys Rev B,2002,66(3):035412.

[8]金子飞，童国平，蒋永进.非邻近跳跃对扶手椅型石墨烯纳米带电子结构的影响[J].物理学报，2009,58(12):8537-8543.

[9]Tong Guoping.Physics and applications of graphene-theory:Chapter 4 the non-neighbor effect in graphene ribbons[M].Croatia:Intech,2011：71-92.

[10]Sun Lian,Li Qunxiang,Ren Hao,et al.Strain effect on electronic structures of graphene nanoribbons:A first-principles study[J].Chem Phys,2008,129(7):074704.

[11]Gui Gui,Li Jin,Zhong Jianxin.Band structure engineering of graphene by strain:First-principles calculations[J].Phys Rev B,2008,78(7):075435.

[12]De-Andres P L,Verges J A.First-principles calculation of the effect of stress on the chemical activity of graphene[J].Appl Phys Lett,2008,93(17):171915.

[13]Harrison W A.Electronic structure and properties of solids[M].San Franciscro:Freeman,1980.

[14]Liu Yang,Han Jie.Electronic structure of deformed carbon nanotubes[J].Phys Rev Lett,2000,85(1):154-157.

[15]Chang Chengpeng,Wu B R,Chen Rongbin,et al.Deformation effect on electronic and optical properties of nanographite ribbons[J].J Appl Phys,2007,101(6):063506.

(责任编辑 杜利民)

Energy-gapcontrolofarmchairgraphenenanoribbonsunderuniaxialstrain

SUN Na, TONG Guoping

(InstituteofCondensedMatterPhysics,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

The electronic energy spectrum and energy gap of armchair graphene nanoribbons under uniaxial strain along the length direction of the ribbon were studied by using the tight-binding approach. When the strain was fixed, for widths 3mand 3m+1, the change of the energy gaps with the width of the nanoribbon showed the inflexion points of zero energy gaps and the points moved toward the small width as the non-neighbor hopping was taken into account gradually. When the width was narrowed, whether the non-neighbor hopping was included or not, there was inflexion point when the third neighbor was included for width 3mapart from 3m+2. But the inflexion points appeared as increasing of the widths apart from the nearest neighbor of width 3m+1.

graphene nanoribbons; tight-binding approach; uniaxial strain; energy gap

O481.1

A

1001-5051(2013)02-0176-06

2012-05-02

国家自然科学基金资助项目(20804039)

孙 娜(1985-)，女，湖北襄阳人，硕士研究生.研究方向：凝聚态理论.

童国平.E-mail: tgp6463@zjnu.cn.