带有临界指数的非齐次Klein-Gordon-Maxwell方程解的存在性*
2013-10-25赵婧琳沈自飞
赵婧琳, 沈自飞
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
带有临界指数的非齐次Klein-Gordon-Maxwell方程解的存在性*
赵婧琳, 沈自飞
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
主要研究了以下一类非齐次Klein-Gordon-Maxwell方程:
解的存在性.在g(x)满足一定的假设条件下,通过变分方法得出系统解的存在性结论.
Klein-Gordon-Maxwell 方程;山路引理;变分方法;非齐次;Ekland变分原理
0 引 言
主要研究了一类非齐次Klein-Gordon-Maxwell方程
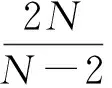
本文主要讨论了当g(x)≠0,即方程组为非齐次方程组时解的存在性问题,并得到了方程组至少有2个解,且其中有一个为局部极小值解的结论.
本文的主要结论是下面的定理:

1 预备知识

系统(2)具有变分结构,考虑泛函F:H1(R3)×D1,2(R3)→R,
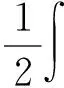
类似于文献[1]中所用的方法,为了克服泛函本身的无界性,需要对泛函进行一些简化.
引理1(u,Φ)是系统(2)的弱解当且仅当它是F在H1(R3)×D1,2(R3)上的临界点.
证明 由F∈C1(H1(R3)×D1,2(R3),R)知,对于∀ξ∈H1(R3),η∈D1,2(R3),F的偏导形式为
由式(4)知,结论显然成立.引理1证毕.
引理2对于每一个u∈H1(R3),存在唯一的φ=φu∈D1,2(R3),使得系统(2)中的第2式成立.映射Φ:u∈H1(R3)→φu∈D1,2(R3)是连续可导的,且
1)在集合{x|u(x)≠0}上,-ω≤φu≤0;

证明 1)由文献[1,4]直接可得.
2)为了证明性质2),将系统(2)中的第2式左右同时乘以φu,并分部积分,得

由于 -ω≤φu≤0,因此,

于是
‖φu‖D1,2≤cω‖u‖2≤c‖u‖2.
引理2证毕.

1)ψu是下面方程的解:

2)ψu≤0.
由引理1~引理3可以将泛函进行简化,考虑泛函E:H1(R3)→R,E(u)=F(u,Φ),
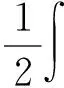
E是C1(R3)的,对任意的u,v∈H1(R3),有

引理4[1]以下结论是等价的:
1)(u,φ)∈H1(R3)×D1,2(R3)是F的临界点;
2)u是E的临界点,且φ=φu.
2 定理1的证明

证明 由式(6)及引理2知


‖u‖(a1‖u‖-a2‖u‖2*-1-‖g(x)‖L).
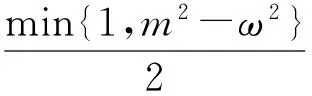
引理6存在v1∈H1,‖v1‖>ρ,使得E(v1)<0.
证明 由式(6)及引理2可知


(8)
由式(8)可知,存在v1=t1u,当t1>0且充分大时,E(v1)<0.引理6证毕.
由引理5和引理6及山路引理可知,存在序列{un}⊂H1(R3),使得

引理7序列{un}有界.
证明 由式(6)、式(7)和式(9)可知



当t>0充分小时,易得E(tψ)<0,且
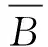



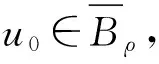
[1]Benci V,Fortunato D.Solitary waves of the nonlinear Klein-Gordon equation coupled with the Maxwell equations[J].Rev Math Phys,2002,14(4):409-420.
[2]Benci V,Fortunato D.The nonlinear Klein-Gordon equation coupled with the Maxwell equations[J].Nonlinear Anal,2001,47(9):6065-6072.
[3]D′Aprile T,Mugnai D.Solitary waves for nonlinear Klein-Gordon-Maxwell and Schrödinger-Maxwell equations[J].Proc Royal Soc Edinburgh:A,2004,134(5):893-906.
[4]D′Aprile T,Mugnai D.Non-existence results for the coupled Klein-Gordon-Maxwell equations[J].Adv Nonlinear Stud,2004,4(3):307-322.
[5]Azzollini A,Pomponio A.Ground state solutions for the nonlinear Klein-Gordon-Maxwell equations[J].Topol Meth Nonlinear Anal,2010,35:33-42.
[6]Cassani D.Existence and non-existence of solitary waves for the critical Klein-Gordon equation coupled with Maxwell′s equations[J].Nonlinear Anal,2004,58(7/8):733-747.
(责任编辑 陶立方)
SolutionsfornonhomgeneousKlein-Gordon-Maxwellequationswithcriticalexponent
ZHAO Jinglin, SHEN Zifei
(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)
The existence of solutions for a class of nonhomgeneous Klein-Gordon-Maxwell equations as follows was studied,
Under some assumptions on the nonhomgeneous itemg(x), the existence results of solutions for the system was obtained by variational methods.
Klein-Gordon-Maxwell equations; moutain pass theorem; variational methods; nonhomogeneous; Ekland variational principle
O175.25
A
1001-5051(2013)02-0146-04
2012-11-24
国家自然科学基金资助项目(11271331)
赵婧琳(1987-),女,河南信阳人,硕士研究生.研究方向:非线性泛函分析.
