灰色预测GM(1，1)模型的Matlab实现

朱登远，常晓凤

(1.长安大学公路学院，陕西西安 710064;2.长安大学信息工程学院，陕西 西安 710064)

灰色系统理论是20世纪80年代由我国邓聚龙教授提出的一种数学方法，可用来解决小样本的信息不完备系统的复杂问题，在岩土工程中得到了广泛关注［1－2］。如果有一个程序能够使工程人员只需输入数据，而不需编写计算公式，就可以得到分析预测结果，将会使灰色系统理论更好地应用在岩土工程中，因此有必要对其进行编程和算法实现，使其程序化、智能化。

在Matlab语言系统中，几乎所有的操作都是以矩阵操作为基础，而在灰色模型预测过程中，需要进行大量的矩阵运算，Matlab在这方面显示了独到之处。将Matlab和灰色模型结合，可以实现系统预测，提高计算的效率［2］。国内外学者结合相关领域做了一些研究并取得了很大进展。张艳萍［3］研究了基于Matlab的灰色系统预测，并结合广东省批发零售业预测进行了GM(1，1)模型的Matlab实现;曹玉珍［4］进行了基于Matlab的GM(1，1)模型在广州市降尘预测中的应用研究;彭利平［5］进行了基于Matlab的GM(1，1)模型在机械工业中的应用研究;李朝阳［6］进行了基于Matlab的GM(1，1)模型的大气污染物浓度预测;梁智勇［7］用Matlab实现了GM(1，1)模型的供电量预测;陈刚［2］研究了GM(1，1)模型在建筑物沉降预测中的应用及Matlab实现;唐丽芳［8］和周亚非［9］分别结合某高校教师人数预测和住宿餐饮业收入增加值预测研究了GM(1，1)模型的Matlab实现及其应用。虽然这些学者都对GM(1，1)模型进行了研究，并在此基础上给出了对应的Matlab算法，但由于各种原因，算法表达各不相同、不够全面且不规范，其正确性没有得到很好验证，有的算法用Matlab运行出现错误，无法使用。笔者在此基础上研究分析，综合其优点、改正不必要的细节和错误，重新整理编写GM(1，1)模型Matlab算法，以增强Matlab在GM(1，1)模型灰色预测中的实用性和通用性，方便工程人员使用。

1 GM(1，1)模型原理

灰色预测GM(l，l)模型是一个拟微分方程的动态系统［10］，其建模的实质是对原始数据先进行一次累加生成，使生成的数据序列呈现一定规律，而后通过建立一阶微分方程模型，求得拟合曲线，用以对系统进行预测。具体过程如下：

(1)给定原始序列

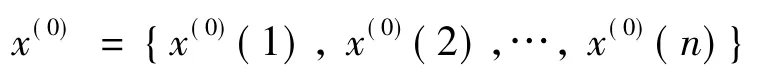
(2)1－AGO生成序列

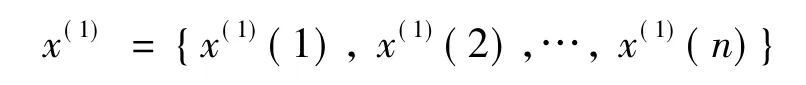
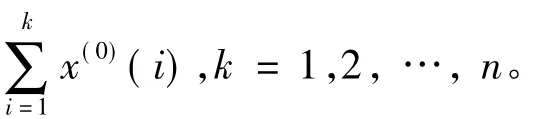
(3)紧邻均值生成序列

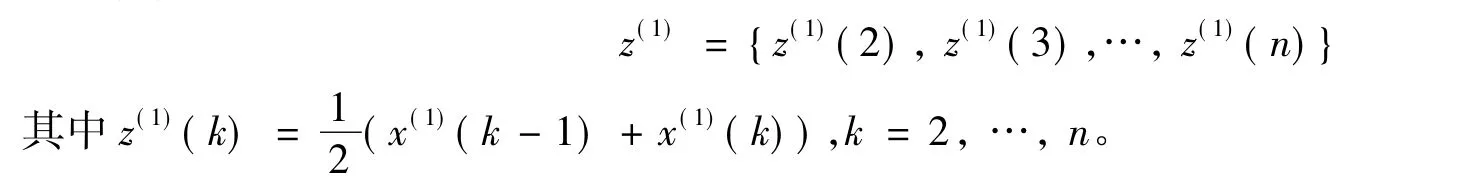
(4)建立灰色微分方程

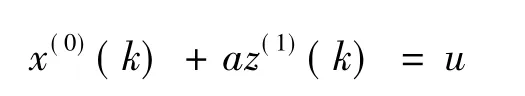
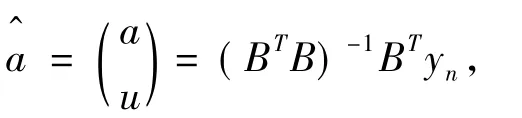
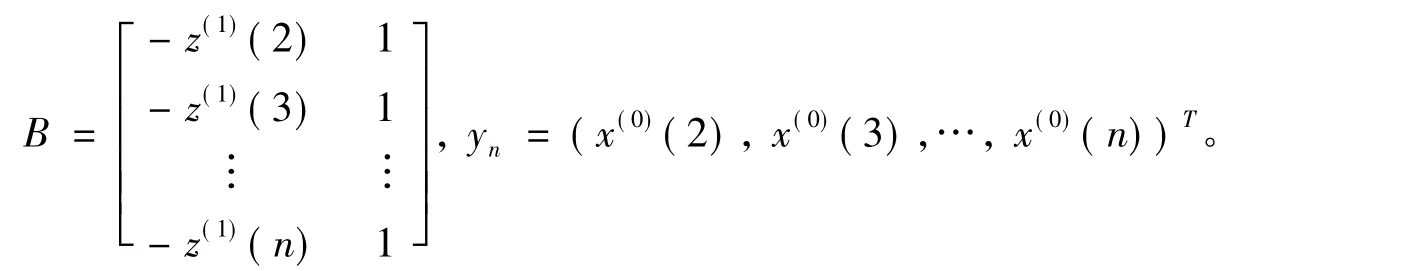
(5)对应的白化方程为

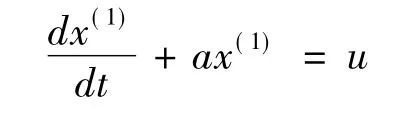
(6)解的离散化形式为

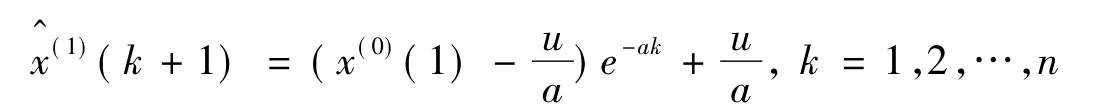
(7)I－AGO还原序列

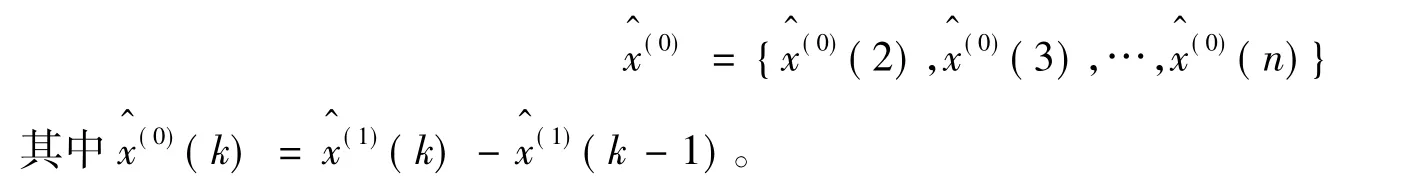
2 模型精度检验

(1)残差检验。

绝对残差序列

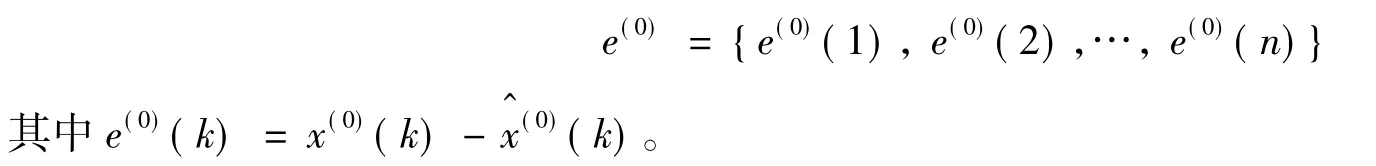
相对残差序列

平均误差

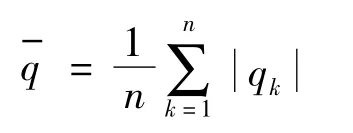
(2)后验差检验。

原始数据的平均值、均方差计算

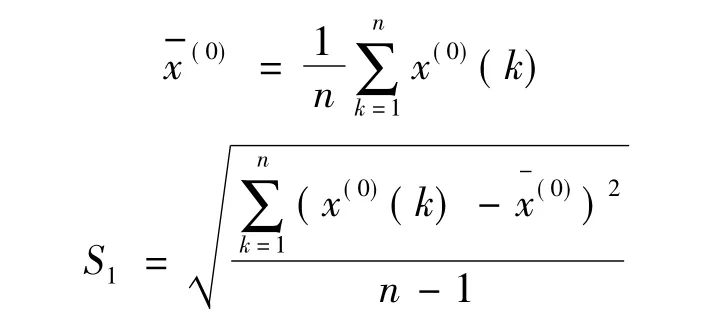
绝对残差的平均值、均方差计算

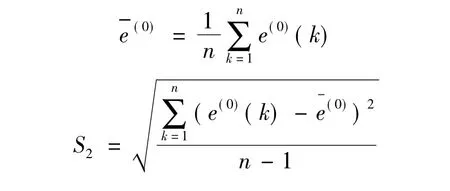
后验差比值计算

小误差概率计算

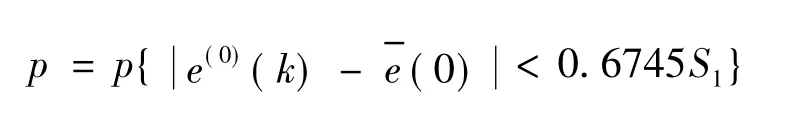
(3)关联度检验。

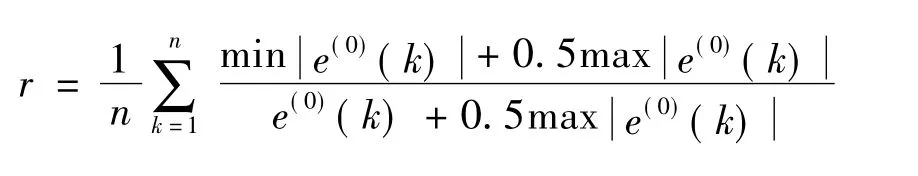
表1 模型精度检验标准［11］

3 Matlab算法实现

4 应用实例分析

为了检验GM(1，1)模型的Matlab算法正确性与通用性，选用以下两个实例进行验证。

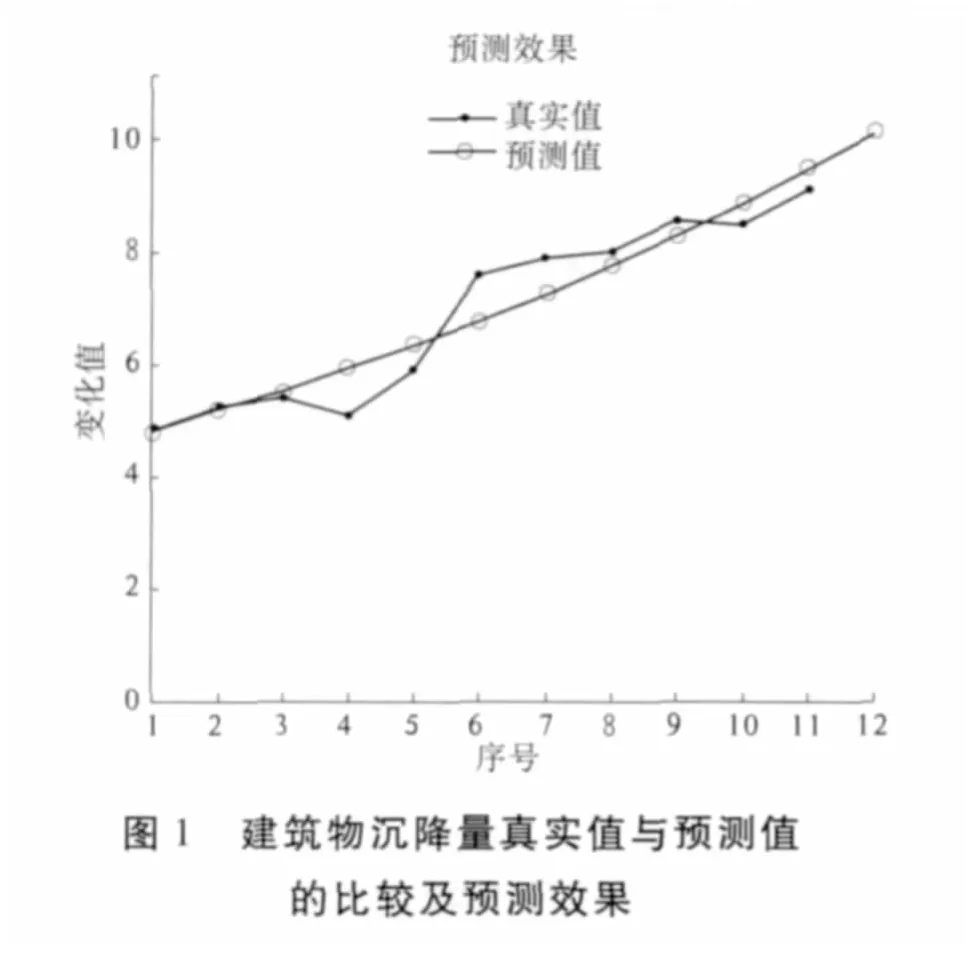
实例1：已知有11个月的某建筑物沉降观测数据，现建立GM(1，1)模型，进行模型精度检验，并对12 月份的沉降量进行预测，实际观测数据如表 2 所示。显然，x0=［4.8，5.2，5.4，5.1，5.9，7.6，7.9，8.0，8.6，8.5，9.1］，x=［1，2，3，4，5，6，7，8，9，10，11，12］。

表2 某建筑物沉降量观测数据

Matlab 运行结果：xx0=［4.800 0，5.176 7，5.536 8，5.921 9，6.333 9，6.774 5，7.245 7，7.749 8，8.288 9，8.865 5，9.482 2，10.141 8］，e0=［0.000 0，0.023 3，－ 0.136 8，－ 0.821 9，－ 0.433 9，0.825 5，0.654 3，0.250 2，0.311 1，－ 0.365 5，－ 0.382 2］，averq=0.055 3，C=0.391 2，p=1，r=0.639 2，相对误差检验为三级，后验差检验为二级，关联度检验为四级。沉降量真实值与预测值的比较及预测效果如图1所示。

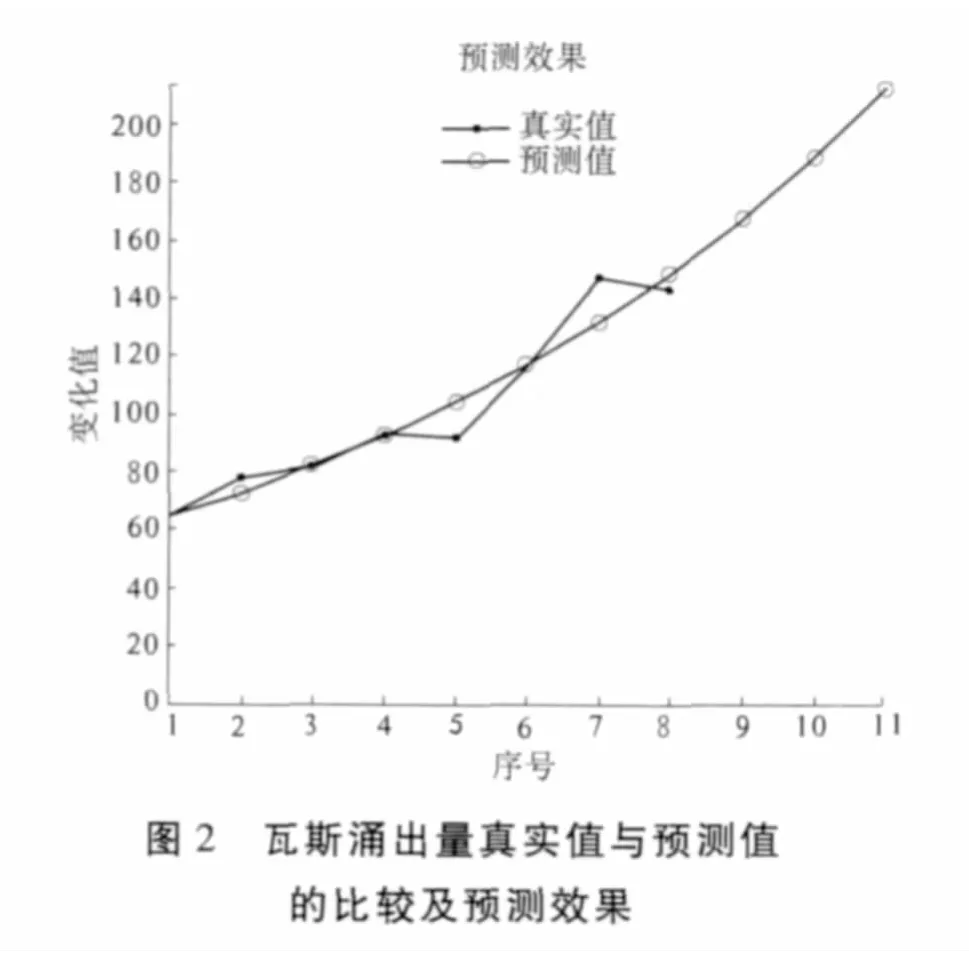
实例2：已知有8个月的某矿瓦斯涌出量记录数据，现建立GM(1，1)模型，进行模型精度检验，并对9、10和11月份的瓦斯涌出量进行预测，相关记录数据如表 3所示。显然，x0=［65.08，77.97，81.89，93.16，92.31，116.16，147.25，143.26］，x=［1，2，3，4，5，6，7，8，9，10，11］。

Matlab 运行结果：xx0=［65.080 0，72.875 4，82.085 3，92.459 2，104.144 1，117.305 6，132.130 6，148.829 1，167.637 9，188.823 8，212.687 1］，q= ［0，0.065 3，－ 0.002 4，0.007 5， － 0.128 2，－0.009 9，0.102 7，－0.038 9］，averq=0.044 4，C=0.305 2，p=1，r=0.885 0，相对误差检验为二级，后验差检验为一级，关联度检验为二级。瓦斯涌出量记录值与预测值的比较及预测效果如图2所示。

表3 某矿瓦斯涌出量记录数据

上面2个实例分别与文献［2］和［12］中的计算结果相同，充分证明了Matlab算法的正确性与通用性，减少了工程人员的编程和计算繁琐，能够较为快速、精确地进行计算，以及对所得数据的准确性分析和预测。

5 结论

灰色模型的公式化特点和Matlab独特的计算优点，使灰色预测建模和Matlab算法得到了很好结合。本文基于灰色系统理论基本原理，用Matlab建立了GM(1，1)模型算法，实现了Matlab在灰色预测中的应用。GM(1，1)模型的Matlab算法为建立其他相应的灰色模型提供了参考和依据，若将所有灰色模型编制成一个通用Matlab软件包，则可实现灰色理论的程序化、智能化。工程人员只需输入数据，而不需编写计算公式，就可以得到分析预测结果，减少了工程人员的工作量，在工程上具有一定的实用价值。GM(1，1)模型的Matlab算法具有一定的通用性，但精密性和细微之处有待进一步的完善和验证。

［1］李恒凯，刘传立.基于灰色理论的变形智能预测模型库研究［J］.岩土力学，2011，32(10)：3119－3124.

［2］陈刚，王波，邓哲.GM(1，1)模型在建筑物沉降预测中的应用及Matlab的实现［J］.城市勘测，2011(1)：107－109.

［3］Zhang Yanping，Li Mingsheng.Grey System Forecasting Based on MATLAB and Its Example Application［J］.2011(1)：107－109.

［4］曹玉珍，莫翠云，蔡明.基于MATLAB的灰色模型在广州市降尘预测中的应用［J］.中国环境监测，2006，22(5)：54－56.

［5］彭利平，颜於滕，黄剑，等.基于Matlab的灰色GM(1，1)模型在机械工业中的应用探究［J］.煤矿机械，2009，30(12)：63－65.

［6］李朝阳，魏毅.基于MATLAB灰色 GM(1，1)模型的大气污染物浓度预测［J］.环境科学与管理，2012，37(1)：48－53.

［7］梁智勇.用Matlab实现GM(1，1)灰色模型的供电量预测［J］.电脑编程与维护，2009(24)：93－102.

［8］唐丽芳，贾冬青，孟庆鹏.用MATLAB实现灰色预测GM(1，1)模型［J］.沧州师范专科学校学报，2008，24(2)：35－37.

［9］周亚非.GM(1，1)的MATLAB实现及其应用［J］.长春师范学院学报：自然科学版，2010，29(1)：32－35.

［10］于国芳.地基变形的灰色预测模型［J］.西部探矿工程，2009(2)：11－13.

［11］仇环，曲国庆，苏晓庆.GM(1，1)模型的改进［J］.山东理工大学学报：自然科学版，2008，22(2)：32－35.

［12］胡永梅.灰色系统GM(1，1)模型在煤矿瓦斯涌出量预侧中的应用［J］.能源与环境，2008(4)：45－46.