人工神经网络在边坡稳定分析中的应用

翟永勇

(江苏华东建设集团有限公司，江苏南京 210007)

随着我国经济的蓬勃发展，重大项目如水电、露天采矿等项目相继上马。这些重大工程的建设，由于受到规模宏大及场地的限制，经常需要在复杂地质环境条件下，开挖各种各样的高陡边坡［1］。因实际地质环境条件的不同，边坡工程因地而异、复杂多变。这种变异性与复杂性容易使得边坡性质及稳定性呈现出很大的非线性关系，给边坡稳定性分析带来很大困难。

现有的资料［2－4］显示边坡的破坏会对国民经济建设和社会发展造成重大损失。边坡工程是一类典型的岩土工程，边坡稳定性分析与评价是边坡工程的核心内容之一，它贯穿于边坡工程的始终［5］。边坡稳定分析是经典土力学最早试图解决而至今仍未圆满解决的课题［1］。目前在实际工程应用中，评价边坡稳定的普遍性方法是基于极限平衡理论的条分法，且传统条分法有十几种之多［6］，而且其中的一些计算方法还进行了改进［7］。这种方法通过细分土条和假定条间力分布与参数的形式，取任意的滑动面，建立安全系数的抗滑力矩和滑动力矩之比，或者抗剪强度和剪应力之比。通常假定不同的滑裂面，经计算求得土坡稳定的不同安全系数后，得到最小的安全系数值，将其作为土坡安全稳定的安全评价的依据［8］。这种方法以一定的假设条件为前提，可以看出这种方法受到人为因素的影响，会给边坡的稳定分析效果带来一定的影响。

边坡失稳的因素包括地质、地下水、外部环境等因素［9］。边坡工程是一个复杂的非线性系统，其已知量与未知量之间是非线性关系。本文将人工神经网络应用到边坡稳定性分析中。人工神经网络是基于模拟生物大脑结构和功能的一种信息处理系统，具有较好的容错性、高度非线性映射以及自适应、自组织学习的能力，能够捕捉边坡稳定性与影响边坡稳定因素之间的相关规律，反映边坡工程的特性，弥补传统方法在分析边坡稳定性上面的不足，实现对边坡稳定性的分析。

1 人工神经网络

人工神经网络(Artificial Neural Network，简称ANN)的研究始于20世纪40年代。它是在现代神经科学研究成果的基础上，依据人脑基本功能特征，利用工程技术手段模拟生物神经系统的功能或结构而发展起来的一种新型信息处理系统或计算体系［10］。人工神经网络以大规模集团运算为特征，在使用性能上表现出良好的容错性，在功能行为上表现出自组织、自学习的自适应能力，是一个能处理知识背景不清楚、推理规则不明确等复杂类型模式识别问题的大规模非线性系统［10－11］。

1.1 BP人工神经网络

在已有的人工神经网络模型中，应用最为广泛和成熟的是误差反向传播网络，即BP人工神经网络。BP人工神经网络于1986年由Rumelhant和McClellan提出。20世纪80年代末开始在土木工程领域得到应用［12－14］，并取得了良好的效果。到目前为止，在岩土和结构的应用过程中，大多采用的是BP人工神经网络模型。

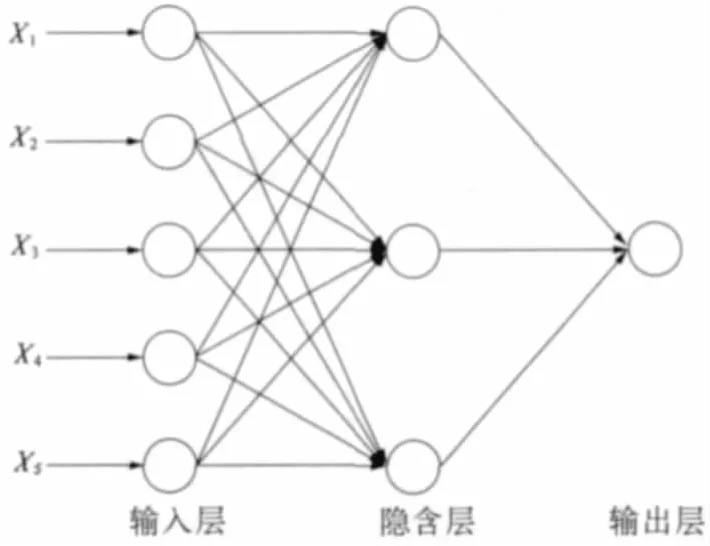
图1 神经网络模型

1.2 BP人工神经网络模型

本文建立的边坡稳定分析模型结构如图1所示，由输入层、隐含层和输出层组成。

1.2.1 输入层

各层神经元个数的选择对网络的性能影响很大。该层神经元的个数等于输入向量的分量维数。本文选取文献［13］中已经研究清楚且其稳定性状况已有明确结论的23个边坡样本作为研究对象，边坡的稳定性有稳定和破坏两种状态，其中1～20为训练样本，21～23为测试样本。为方便表示，X1表示边坡土体的重度，X2表示边坡土体的粘聚力，X3表示边坡土体的内摩擦角，X4表示边坡土体的坡角，X5表示边坡土体的高度(如表1所示)。

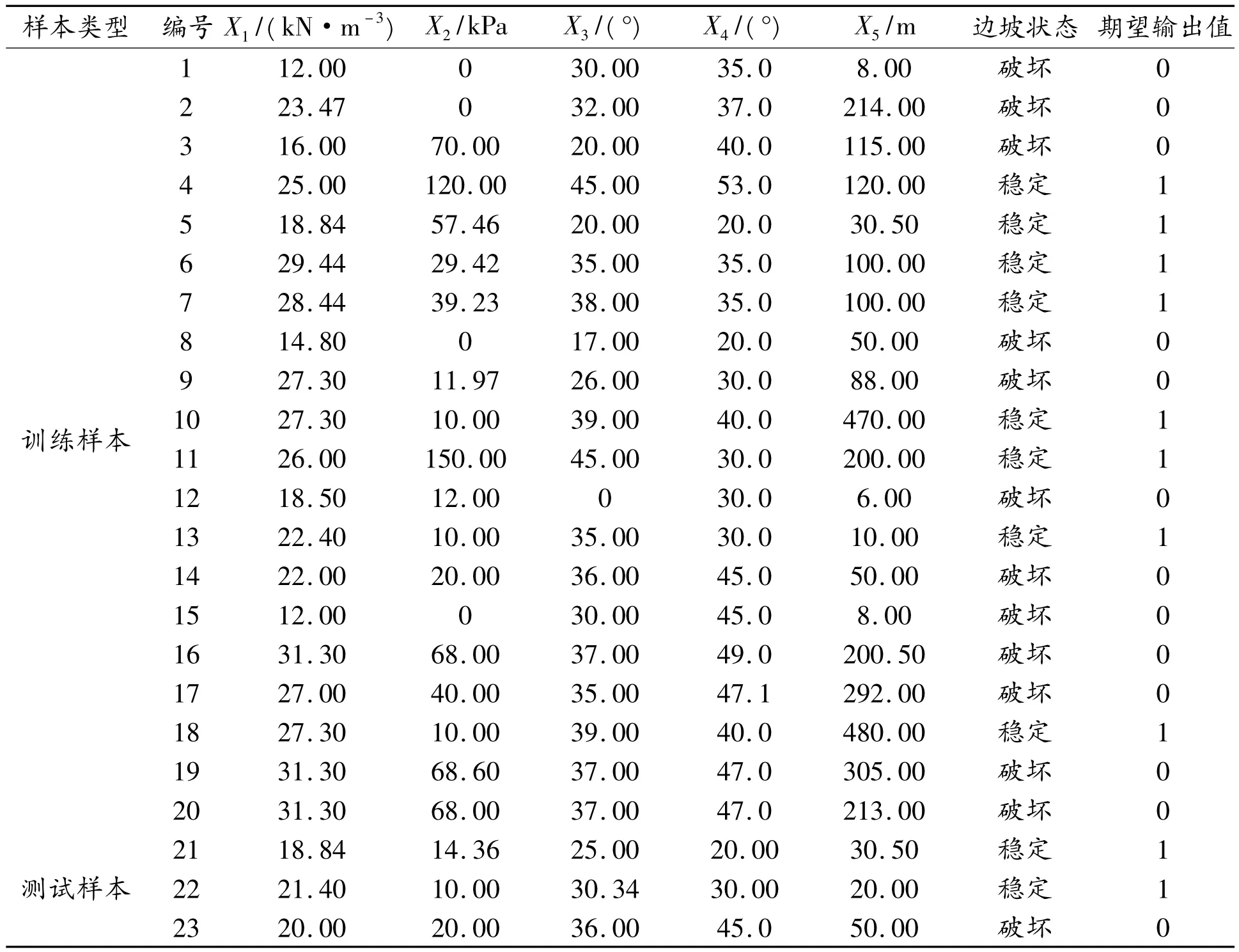
表1 边坡稳定性分析输入值

1.2.2 输出层

该层神经元个数为1个，输出向量是边坡稳定状态代码。若输出代码为1，表示边坡处于稳定状态;若输出代码为0，则表示边坡为破坏状态。

1.2.3 隐含层

隐含层神经元个数的选择直接关系到神经网络的规模和精度，其确定方法有直接定型法、修剪法和生长法等三种，根据实际的需要，本文采用Kolmogorov定理：如果输入变量的个数为n，那么隐含层神经元个数一般可取为2n+1个。本文中输入向量的维数为5，所以隐含层神经元的个数是11。

1.2.4 归一化公式

网络的初始值对网络的最终结果影响较大，且边坡各个分量的单位不统一，数量级差别也大，为使输出的数据在［0，1］区间，需要在网络训练前将数据进行归一化处理，即

式中：xn、xmin、xmax分别表示原始输入数据、原始输入数据中的最大值和最小值;yn、ymin、ymax分别表示原始输出数据、原始输出数据的最大值和最小值。

2 BP人工神经网络模型及预测

本文应用newff函数建立一个边坡稳定分析BP人工网络模型。在进行网络样本训练时，其中各参数的设定情况为：学习效率设为0.1，网络训练的最大迭代次数为1 000次，其收敛精度设置为0.01。网络的输入层和隐含层均采用对数型S型函数作为传递函数。在样本训练过程中，当网络训练达到所设置的目标精度或满足最大迭代次数时，自动停止训练。

网络学习后，测试样本21～23的结果如表2所示。

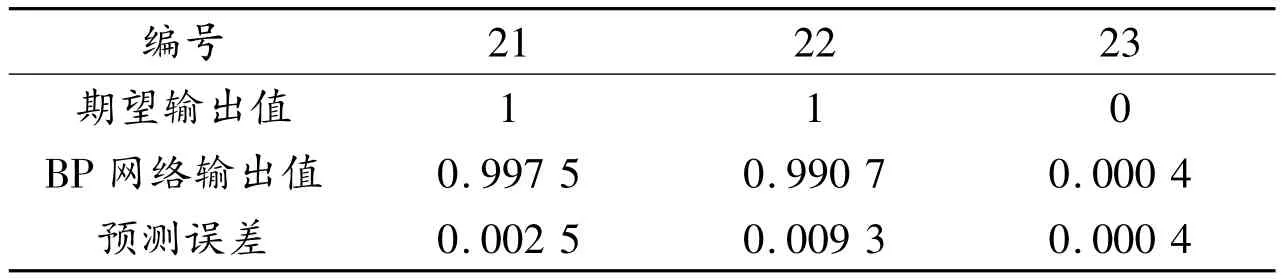
表2 测试样本输出值

从表2可以看出，BP网络输出值和期望输出值相差不大，说明该BP人工神经网络的学习效果较好。由于样本较少，且选取的影响边坡稳定性的因素只有5个，说明预测精度还有进一步提高的空间。随着样本数量的增加，选取的影响因素更符合实际情况，预测模型的预测精度会进一步提高。上述建立的BP人工神经网络模型从工程应用的角度看是合理的。

3 结论和展望

本文将BP人工神经网络应用于边坡稳定分析，BP神经网络模型评价的结果和传统安全系数评价结果基本一致，所以该模型可以应用于边坡稳定分析。但是，本文在进行分析时，对影响边坡稳定的因素只考虑了与地质相关的5个因素，而实际影响边坡稳定性的因素还有很多，诸如含水率、人工活动等。因此，利用BP人工神经网络分析边坡的稳定性还需要进一步的研究。

［1］刘文平，郑颖人，刘元雪.边坡稳定理论及局限性［J］.后勤工程学院学报，2005(1)：15－19.

［2］黄润秋.20世纪以来中国的大型滑坡及其发生机制［J］.岩石力学与工程学报，2007，26(3)：433－453.

［3］刘天翔，杨雪莲，周永江，等.“5.12”汶川大地震诱发边坡地质灾害及其对公路基础设施影响的初步研究［J］.2008(4)：192 －199.

［4］吉随旺，唐永建，胡德贵，等.四川省汶川地震灾区干线公路典型震害特征分析［J］.2009，28(6)：1250－1259.

［5］陈新民，罗国煜.基于经验的边坡稳定性灰色系统分析与评价［J］.岩土工程学报，1999，21(5)：638－641.

［6］Zhu D Y，Lee C F，Jiang H D.Generalised framework of limit equilibrium methods and numerical procedure for slope stability analysis［J］.Geotechnique，2003，53(4)：377 －395.

［7］朱大勇，李焯芬，黄茂松，等.对3种著名边坡稳定性计算方法的改进［J］.岩石力学与工程学报，2005，24(2)：183－194.

［8］王轶昕，王国体，方诗圣.边坡稳定和滑坡实例计算对比分析［J］.合肥工业大学学报：自然科学版，2011，34(5)：721－724.

［9］牟瑞芳.边坡稳定性分析与加固技术研究［D］.成都：西南交通大学，2002.

［10］冯夏庭.智能岩石力学导论［M］.北京：科学出版社，2000.

［11］傅鹤林，彭思甜，韩汝才，等.岩土工程数值分析新方法［M］.长沙：中南大学出版社，2006.

［12］高浪，谢康和.人工神经网络在岩土工程中的应用［J］.土木工程学报，2002，35(4)：77－81.

［13］刘勇健，李子生.人工神经网络在岩土工程中的应用综述［J］.广东工业大学学报，2004，21(4)：66－71.

［14］杨二静.人工神经网络和遗传算法在岩土及结构工程中的应用研究［D］.南宁：广西大学，2007.