一种碳酸盐岩储层横波速度估算方法

刘欣欣，印兴耀，张 峰

(1.中国石油大学地球科学与技术学院，山东青岛 266580;2.中国石油大学地球物理与信息工程学院，北京 102249)

碳酸盐岩储层是重要的油气勘探目标。该类储层非均质性很强，孔隙度、渗透率和储层其他特性之间的关系非常复杂，导致储层特征描述困难［1］。横波速度有利于储层岩性、物性和含油气性的分析与识别，在叠前地震反演、AVO属性分析、测井岩性解释以及多波资料解释等过程中都有非常重要的作用。由于横波测井成本高，解释难度大等原因，实际生产中许多井资料缺少横波测井信息［2］。基于岩石物理理论的方法是计算地震横波速度的重要手段，许多学者通过岩石物理试验和分析建立了多种经验关系［3-4］及理论模型［5-7］。目前，国内相关研究主要侧重于使用测井或其他资料约束提高横波速度计算精度或者改善实际应用效果［8-12］。针对碳酸盐岩储层的特殊性和复杂性，Kumar等［13-14］研究了孔隙几何形状对横波速度的影响，提出了估算不同类型孔隙的纵横比和孔隙度的方法。Vega等［15］研究了非均质碳酸盐岩中流体置换模型的适用性，指出斑块饱和模型能预测更大的速度变化。笔者根据岩石物理理论和模型计算饱和岩石的横波速度，讨论碳酸盐岩中孔隙微结构参数和矿物组分弹性模量的求取方法，进而确定岩石的孔隙结构和岩性参数，并在此基础上计算横波速度。

1 碳酸盐岩储层横波速度计算原理

岩石是由固体的岩石骨架和流动的孔隙流体组成的双相体，在波长远远大于岩石的不均匀尺度时，岩石的弹性性质等效于双相体的等效弹性性质［16］。根据岩石物理多孔介质理论，针对碳酸盐岩储层岩性和孔隙结构的复杂性，考虑岩石矿物组分、孔隙微结构、孔隙流体的影响，采用不同的岩石物理理论分别计算碳酸盐岩储层的岩石基质、干燥岩石骨架以及饱和岩石的等效弹性模量，进而计算储层的横波速度。

1.1 岩石基质等效弹性模量计算

Hashin和Shtrikman(1963)提出不同组分混合弹性体模量的最低上限和最高下限(HS界限)［17］。图1是用不同理论计算的方解石和泥质组成的岩石基质的体积和剪切模量。HS上下限比Voigt和Reuss界限范围要窄。在没有足够的信息的情况下，近似使用HS上下限的平均来计算岩石基质的弹性模量。

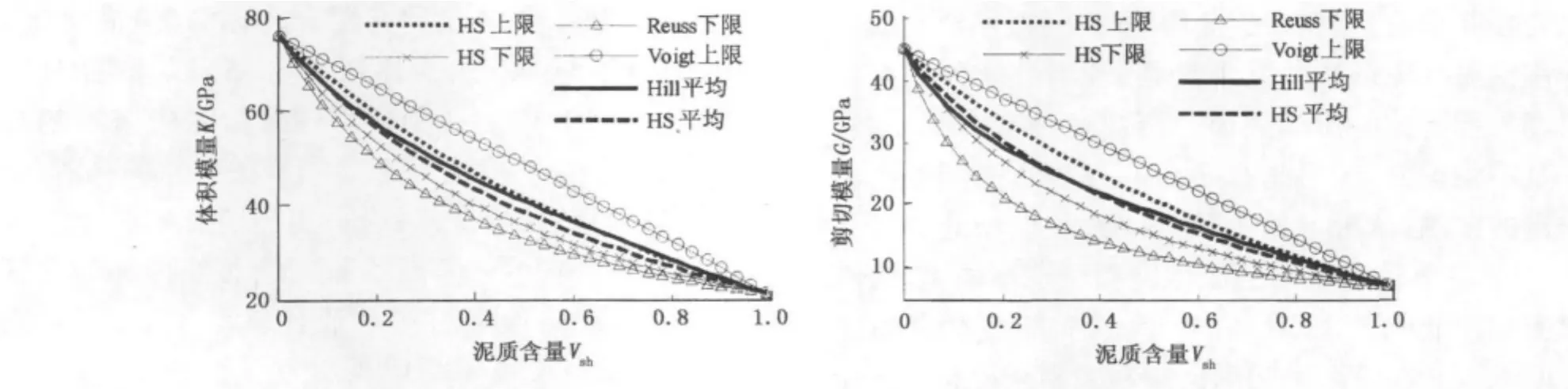
图1 不同等效介质模型计算的岩石基质体积模量和剪切模量Fig.1 Bulk modulus and shear modulus of rock matrix calculated by different effective medium models

1.2 岩石干燥骨架等效弹性模量计算

Kuster等［18］假设孔隙为椭球形，基于散射理论推导出岩石的体积模量K、剪切模量G与孔隙度和孔隙纵横比的联系(KT模型)，令M=(K，G)，T=(P，Q)，则有

式中，φi为第 i种孔隙的体积分数;Mi=(Ki，Gi)，Ki和Gi分别为孔隙内含物的体积模量和剪切模量;Mm=(Km，Gm)，Km和Gm分别为背景基质的体积模量和剪切模量;系数 Tmi=(Pmi，Qmi)，Pmi和 Qmi反映第i种孔隙对岩石基质的影响，是孔隙纵横比的函数。

微分有效介质理论(DEM模型)是通过往固体矿物相中逐渐加入包含物相来模拟双相混合物。弹性模量的耦合的微分方程［19］为

Berryman［20］基于弹性波散射理论，推导出含椭圆形包含体的岩石等效弹性模量，提出自相容近似模型(SCA模型):

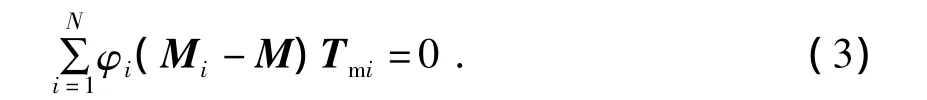
使用以上三种模型计算干燥岩石骨架的弹性模量，结果见图2(孔隙纵横比为0.5)。孔隙度较小时，三种模型的计算结果相当。由于KT模型要求孔隙度与孔隙纵横比的比值要远小于1，因此适用于计算较高纵横比或较小孔隙度岩石的有效弹性模量;DEM模型没有考虑孔隙包含物之间散射的影响，而且包含物的加入顺序会影响微分弹性模量的计算结果;SCA模型假设孔隙是相互孤立的，而且波长远大于包含物尺寸，对孔隙较大的岩石是适用的，但是如果孔隙为针状、盘状和硬币状，那么SCA模型的使用必须谨慎。对于纵横比较大(＞0.1)以及纵横比较小(＜0.1)的孔隙，分别使用KT模型和DEM模型计算岩石骨架的弹性模量。

图2 不同模型计算的干燥岩石骨架体积模量(左)和剪切模量(右)Fig.2 Bulk modulus and shear modulus of dry rock frame calculated by different effective medium models

1.3 饱和岩石的等效弹性模量的计算

Gassmann方程假设岩石宏观上均匀分布，孔隙之间相互连通，但在碳酸盐岩地层中，胶结或者溶蚀作用使得孔隙形状非常不规则，或者填隙物的存在堵塞局部流体的流动通道，导致孔隙流体部分饱和并且不均匀分布，因此Gaussman方程的适用性受到一定的限制。White给出了斑块饱和模型的定量计算［21］。在不同斑块内的流体饱和状态不同，当岩石渗透率较低或者含水饱和度增大时，诱发的孔隙压力增量不能在完全饱和的斑块和未完全饱和的斑块之间达到平衡，从而使岩石骨架硬化，此时岩石体积模量增大而剪切模量保持不变［22］。假设岩石孔隙中填充油、气、水三相流体的混合物，各相流体饱和度分别为Sf1、Sf2、Sf3，斑块饱和模型将不均匀分布的各相流体分开处理，首先分别计算各相流体单独分布时岩石的弹性模量:

使用上述模量的等效平均计算斑块饱和岩石的等效弹性模量:

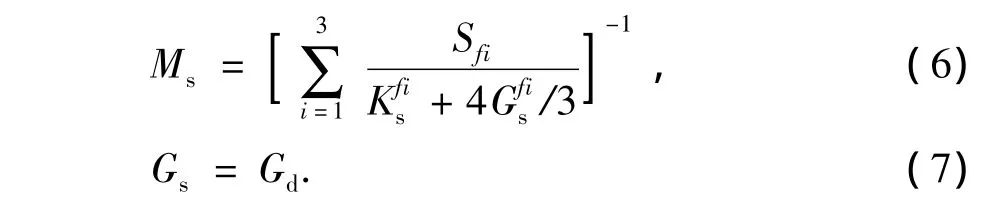
2 关键参数的求取

2.1 碳酸盐岩孔隙微观结构参数计算

孔隙形状是影响碳酸盐岩石弹性的重要参数［23-24］。国内外关于碳酸盐岩孔隙出现了多种分类方法(Lucia，1995;L∅n∅y，2006)［25-26］。考虑到碳酸盐岩孔隙形状，本文将孔隙分为孔洞(纵横比0.5～1.0)、粒间孔隙(纵横比0.1～0.5)以及裂隙(纵横比0.01～0.1)。孔洞代表碳酸盐岩中坚硬的近圆形孔隙或溶洞，裂隙代表岩石中最柔软的孔隙，受到外力作用时易闭合，对岩石速度的影响较大。在含有泥质的情况下，考虑孔隙的连通性再细分出第四种孔隙:泥质孔隙，主要代表含束缚水或者不连通孔隙。则总孔隙度φ可以表示为

式中，φvu、φin、φcr、φcl分别表示孔洞、粒间孔隙、裂隙、泥质孔隙的孔隙度。假设四种孔隙的纵横比分别为 αvu、αin、αcr、αcl。

对于泥质孔隙，根据Xu-White模型对其进行描述。碳酸盐岩中只含有粒间或者晶间孔隙(纵横比约为0.1)时，根据DEM理论计算的纵波速度与Wyllie时间平均方程的计算结果非常接近;对于铸模孔隙或者孔洞等圆形孔隙(纵横比约为1)，DEM理论计算的纵波速度接近于HS上边界;而对于裂隙(纵横比大约为0.01)，DEM理论计算的纵波速度接近于HS下边界［23］。为此使用下面的方法计算这三种孔隙的纵横比:

(1)给定初值条件。假设孔洞、粒间孔隙、裂隙的孔隙纵横比α分别为0.8、0.1、0.01;

(2)假设岩石的全部孔隙为孔洞，分别据DEM理论、HS上限计算岩石纵波速度，得两速度的差ΔvP;

假设岩石的全部孔隙为粒间孔隙，使用DEM理论、Wyllie时间平均方程计算纵波速度，得ΔvP;

假设岩石的全部孔隙为裂隙，使用DEM理论、HS下限计算纵波速度，得ΔvP;

将实测纵波速度与Wyllie时间平均方程计算的纵波速度之差作为纵波速度偏差，该偏差是由于不同的孔隙类型引起的，正偏差代表铸模孔隙等较大纵横比孔隙的影响，零偏差代表粒间孔隙的影响，而负偏差表示裂缝或者高含气量的影响［27］。统计正、零、负速度偏差三者的比例，作为孔洞、粒间孔隙、裂隙三种孔隙分配的初始比例。根据实测纵波速度ΔvPm，计算这三种孔隙的孔隙度:

(1)按照初始比例对除泥质孔隙以外的孔隙进行分配，得到三种孔隙的初始孔隙度φvu、φin、φcr;

(2)计算岩石的纵波速度，得ΔvPe，计算其与实测纵波速度ΔvPm的差ΔvP;

若ΔvP＞ε，则φcr=φcr+Δφ，且① 若 φvu＞0，φvu=φvu-Δφ;② 若φvu=0，则φin=φin-Δφ。转步骤(3);

若ΔvP＜ -ε，则 φvu=φvu+Δφ，且① 若 φcr＞0，φcr=φcr-Δφ;② 若φcr=0，则φin=φin-Δφ。转步骤(3)。

使用上述方法可求取四种孔隙度各自的纵横比和孔隙度，也就得到了碳酸盐岩孔隙微结构参数，然后对于不同纵横比的孔隙，使用KT模型和DEM模型计算干燥岩石骨架的等效弹性模量。

2.2 岩石矿物组分弹性模量反演

碳酸盐岩矿物组成复杂，包括方解石或白云石，经常混合少量的石英，泥质或无水石膏(硬石膏)，以及其他非碳酸盐自生矿物和陆源碎屑矿物。本文中将碳酸盐岩基质等效为白云石、方解石和泥质等矿物组分的混合物。考虑到随着深度变化，地层的温度和压力、岩石的岩性等都会变化，矿物组分的模量可能随之发生变化，而且在不同地区矿物模量也不是一成不变的。储层纵横波速度在一定程度上反映岩石矿物弹性性质的变化，但是纵横波速度受多种因素的影响，其与矿物组分弹性模量的显函数关系式很难建立。为此，根据纵横波速度计算方法，建立目标函数，通过使其取最小值反演求取各种矿物组分的体积模量K和剪切模量U:

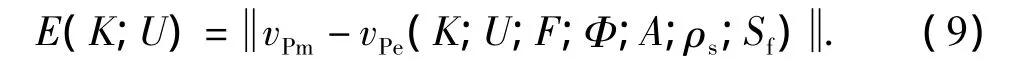
式中，K=(K1，K2，…，KN)，U=(U1，U2，…，UN)分别为N种矿物组分的体积模量和剪切模量;F=(f1，f2，…，fN)为各组分的体积分数;Φ =(φvu，φin，φcr，φcl)为四种孔隙的孔隙度，A=(αvu，αin，αcr，αcl)为四种孔隙的纵横比;Sf为流体饱和度;ρs为饱和岩石的密度;vPm、vPe分别为实测和计算的纵波速度。

目标函数式(9)取最小值的过程是一个非线性多元函数的求解问题。本文采用自适应遗传算法［28］，利用目标函数本身的信息建立寻优方向，具备全局最优搜索性，且具有内在的并行计算特性。具体的计算流程如图3所示。为了减少多解性，使用矿物组分弹性模量的经验值范围对待求参数进行约束。

使用上述方法可以反演得到随深度变化的矿物组分弹性模量。但是，该过程是建立在孔隙微结构参数已知的基础上的，而确定孔隙微结构参数时，又需要矿物组分的弹性模量值作为输入，这样导致了矿物组分弹性模量和孔隙微结构参数互为前提条件而又互相影响。为此，首先使用矿物组分弹性模量的经验值来计算孔隙微结构参数，据此计算矿物组分的弹性模量。最后利用计算得到的矿物组分弹性模量值和孔隙微结构参数计算储层的横波速度。

图3 矿物组分弹性模量反演流程Fig.3 Flow chart for mineral elastic modulus inversion

3 实际资料应用效果分析

对某碳酸盐岩研究区的实际测井资料进行横波速度计算。该研究区内的碳酸盐岩矿物主要是方解石和白云石，含有少量的泥质。储层内的孔隙流体主要是水和天然气。A井的已知测井数据如图4所示，该井的实测横波速度用于检验横波速度估算结果的质量。

首先计算岩石的孔隙微结构参数。用表1所示矿物组分弹性模量的经验值，计算得到的孔洞、粒间孔隙、裂隙以及泥质孔隙的纵横比和孔隙度分别如图5和图6所示。计算的孔隙微结构是实际孔隙的等效近似，可以在一定程度上反映岩石中不同形状孔隙的组成情况。从图中可以看出，5.34 km深度附近的地层，纵波速度降低，计算的粒间孔隙和裂隙纵横比减小，而孔洞的孔隙度降低，粒间孔隙和裂隙的孔隙度增大，符合低纵横比孔隙导致岩石纵波速度较低的理论趋势。计算得到的横波速度(图7左图)的低频趋势与实测纵横波速度基本吻合，但是高频细节上存在不可忽视的误差。

图4 A井已知测井数据Fig.4 Well logging data of well A

表1 矿物组分经验弹性参数Table 1 Empirical elastic parameters of mineral components

图5 不同孔隙的孔隙纵横比Fig.5 Pore aspect ratio of different pores

根据本文中的方法反演方解石、白云石以及泥质的弹性模量，结果如图8所示。由于方解石含量较高，因此相对于白云石和泥质来说，方解石的弹性模量对纵波速度的影响较大。在不含白云石的深度上，无法反演求取白云石的弹性模量，为此假设其等于表1中所示的经验值。从图中可以看出，在5.46 km深度附近的地层，计算的横波速度比实测横波速度高，而反演得到的矿物组分弹性模量值比经验值小，这与理论趋势相吻合。最终计算的横波速度如图7中右图所示，与图7左图所示的横波速度计算结果相比，大大减小了由于矿物组分弹性模量不准确引入的误差，尤其是在5.46 km深度附近，横波速度的低值得到了很好的反映。

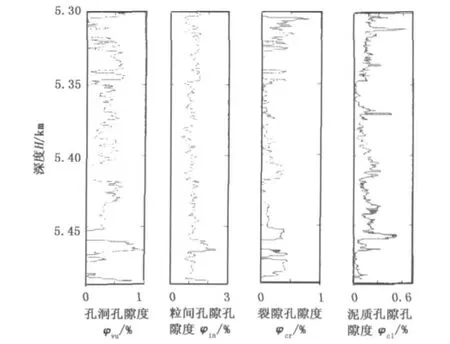
图6 不同孔隙的孔隙度Fig.6 Porosity of different pores

计算的纵波速度与实测值的相关系数为0.99，估算的横波速度与实测值的相关系数为0.94，平均相对误差为1.9%，平均绝对误差为59.9 m/s，方差为77.1 m/s。计算得到的纵横波速度以及泊松比与实测值的吻合程度较高且误差接近于正态分布(图9、10，图10中曲线为高斯分布拟合曲线)证明了方法的有效性。如果结合测井解释信息，可以进一步进行岩性或者流体岩石物理分析，为地震反演或者解释提供有利的帮助和指导。

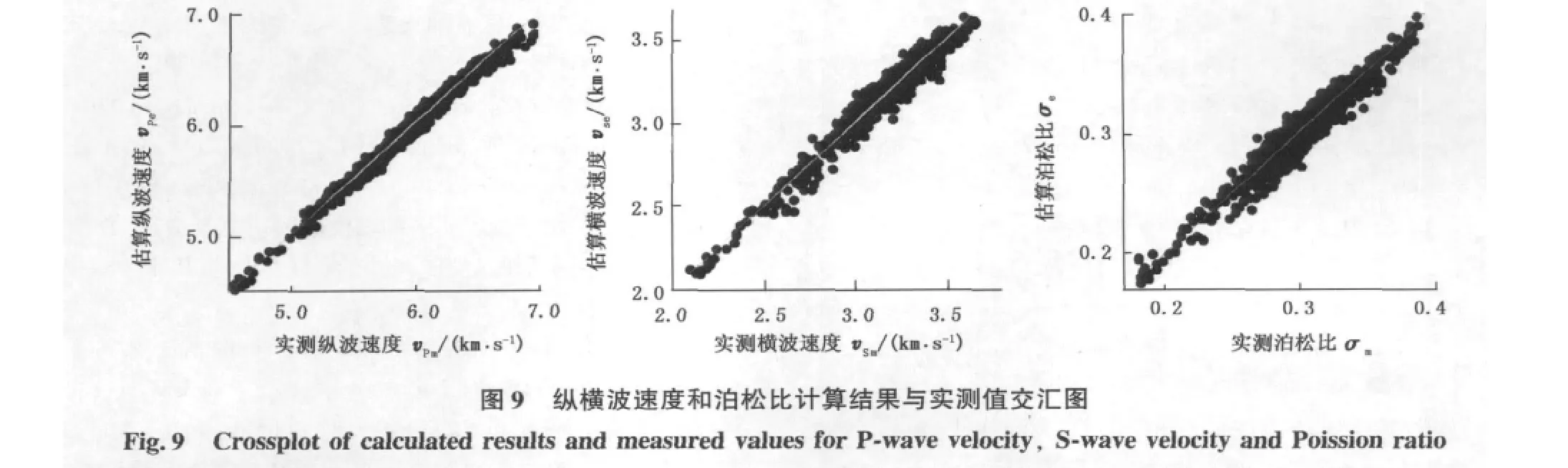
图10 纵横波速度以及泊松比估算结果误差分布直方图Fig.10 Error distribution histogram for P-wave velocity，S-wave velocity and Poission ratio

4 结束语

碳酸盐岩储层的非均质性很强，进行岩石物理分析和计算时，需要明确各种岩石物理理论模型的适用性，建立适用于复杂碳酸盐岩储层的岩石物理理论和方法。对碳酸盐岩孔隙微结构进行合理的描述是计算横波速度的关键。在缺少岩心数据或者试验数据的情况下，根据孔隙形状和连通性对碳酸盐岩孔隙进行划分，得到的孔隙微结构是实际岩石孔隙系统的等效近似，可以在一定程度上反映岩石中不同形状孔隙的构成情况。碳酸盐岩储层的矿物组分非常复杂，使用岩石速度信息作为约束条件反演计算得到的不同深度点上的矿物组分弹性模量，可以在一定程度上反映储层岩性的纵向变化。实际地层中的碳酸盐岩由于裂隙的定向排列可能表现出各向异性特征，由于缺少相关的试验及测井信息，无法对裂隙的方位和密度等作出合理的描述，因此没有考虑裂隙诱导各向异性的影响。相关的各向异性理论和方法有待进一步研究。

［1］ AHR W M，ALLEN D，BOYD A，et.al.Confornting the carbonate conundrum［J］.Oilfield Review，2006，18-29.

［2］ 楚泽涵，陈丰，刘祝萍，等.估算地震横波速度的新方法［J］.测井技术，1995，19(5):313-318.CHU Ze-han，CHEN Feng，LIU Zhu-ping，et al.Estimation of formation Vs［J］.Well Logging Technology，1995，19(5):313-318.

［3］ CASTAGNA J P，BATZLE M L，EASTWOOD R L.Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks［J］.Geophysics，1985，50(4):571-581.

［4］ HAN D H，NUR A，MORGAN D.Effects of porosity and clay content on wave velocities in sandstones［J］.Geophysics，1986，51(11):2093-2107.

［5］ GASSMANN F. Über die Elastizität poroser Medien［J］.Veirteljahrsschrift der Naturforschenden Gesellschaft in Zürich，1951，96:1-23.

［6］ GREENBERG M L，CASTAGNA J P.Shear-wave velocity estimation in porous rocks:theoretical formulation，prelimulation，preliminary verification and applications［J］.Geophysical Prospecting，1992，40(2):195-209.

［7］ XU S Y，WHITE R E.A new velocity model for claysand mixtures［J］.Geophysical Prospecting，1995，43(1):91-118.

［8］ 郭栋，王兴谋，印兴耀，等.横波速度计算方法与应用［J］.油气地球物理，2007，5(3):18-22.GUO Dong，WANG Xing-mou，YIN Xing-yao，et al.The calculation method and application of transverse wave［J］.Petroleum Geophysics，2007，5(3):18-22.

［9］ 邵才瑞，印兴耀，张福明，等.利用常规测井资料基于岩石物理和多矿物分析反演横波速度［J］.地球科学——中国地质大学学报，2009，34(4):699-707.SHAO Cai-rui，YIN Xing-yao，ZHANG Fu-ming，et al.Shear wave velocity inversion with routine well logs based on rock physics and multi-minerals nalysis［J］.Earth Science—Journal of China University of Geosciences，2009，34(4):699-707.

［10］ 张璐.基于岩石物理的地震储层预测方法应用研究［D］.青岛:中国石油大学(华东)地球科学与技术学院，2009.ZHANG Lu.Application of rock physics theory in seismic reservior discrimination［D］.Qingdao:School of Geosciences in China University of Petroleum，2009.

［11］ 李呈呈.碳酸盐岩岩石物理模型的研究及应用［D］.青岛:中国石油大学(华东)地球科学与技术学院，2011.LI Cheng-cheng.The research and application of rock physics model for carbonate rocks［D］.Qingdao:School of Geosciences in China University of Petroleum，2011.

［12］ 周中彪.基于岩石物理模型的测井约束横波速度计算方法研究［J］.物探化探计算技术，2010，32(5):536-541.ZHOU Zhong-biao.The study on S-wave velocity calculation method constrained by logging based on rock physics models［J］.Computing Techniques for Geophysical and Geochemical Exploration，2010，32(5):536-541.

［13］ KUMAR M，HAN D H.Pore shape effect on elastic properties of carbonate rocks［C/OL］.Expanded Abstract of 75th Annual International SEG Meeting，2005，1477-1480.［2010-09-22］ http://dx.doi.org/10.1190/1.2147969.

［14］ BAECHLE G T，COLPAERT A，EBERLI G P et.al.Modeling velocity in carbonates using a dual porosity DEM model［C/OL］.Expanded Abstract of 77th AnnualInternationalSEG Meeting， 2007，1589-1593.［2011-06-23］ http://dx.doi.org/10.1190/1.2792799.

［15］ VEGA S，BERTEUSSEN K，Yue-feng SUN.Is Gassmann1the best model for fluid substitution in heterogeneous carbonates?［C/OL］.Expanded Abstract of 77th Annual International SEG Meeting，2007，1575-1578.［2012-03-29］ http://dx.doi.org/10.1190/1.2792796.

［16］ 陈颙，黄庭芳，刘恩儒.岩石物理学［M］.合肥:中国科学技术大学出版社，2009:17-20.

［17］ BERRYMAN J G.Mixture theories for rock properties［M］//AHRENS T J.A handbook of physical constants.Washington D C:American Geophysical U-nion，1995:205-228.

［18］ KUSTER G T，TOKSÖZ M N.Velocity and attenuation of seismic waves in two-phase media［J］.Geophysics，1974，39(5):587-618.

［19］ BERRYMAN J G.Single-scattering approximations for coefficients in Biot1s equations of poroelasticity［J］.Journal of the Acoustical Society of America，1992，91:551-571.

［20］ BERRYMAN J G.Long-wavelength propagation in composite elastic media［J］.Acoustical Society of America，1980，68(6):1801-1831.

［21］ WHITE J E.Computed seismic speeds and attenuation in rocks with partial gas saturation［J］.Geophysics，2002，67:1406-1414.

［22］ 王炳章，朱晔，王丹.多孔介质的流体机制模型及其频散机理［J］.勘探地球物理进展，2008，31(6):405-413.WANG Bing-zhang， ZHU Ye， WANG Dan.Fluid mechanism models and their velocity dispersions in porous media［J］.Progress in Exploration Geophysics，2008，31(6):405-413.

［23］ ANSELMETTI F S，EBERLI G P.The velocity-deviation log:a tool to predict pore type and permeability trends in carbonate drill holes from sonic and porosity or density logs［J］.AAPG Bulletin，1999，83(3):450-466.

［24］ WEGER R J，BAECHLE G T，MASAFERRO J L，et al.Effects of porestructure on sonic velocity in carbonates［C/OL］.Expanded Abstract of 74th Annual International SEG Meeting，2004，23(1):1774-1777.［2011-10-29］ http://dx.doi.org/10.1190/1.1845169.

［25］ LUCIA F J.Rock-fabric/petrophysical classification of carbonate pore space for reservoir characterization［J］.AAPG Bulletin，1995，79(9):1275-1300.

［26］ LØNØY A.Making sense of carbonate pore systems［J］.AAPG Bulletin，2006，90(9):1381-1405.

［27］ ANSELMETTI F S，EBERLI G P.Controls on sonic velocity in carbonates［J］.Pure and Applied Geophysics，1993，141(2/4):287-323.

［28］ SIVANANDAM S N，DEEPA S N.Introduction to genetic algorithms［M］.New York:Springer Publishing Company，2007.