考虑腐蚀储罐底圈壁板的时变可靠度分析

刘雪云，赵光连，钟诗胜，焦映厚，赵继俊

(1.哈尔滨工业大学机电工程学院，黑龙江 哈尔滨 150001;2.哈尔滨工业大学(威海)船舶与海洋工程学院，山东 威海 264209;3.威海市能源监测中心，山东威海 264209)

常压储罐因长期遭受内外介质的腐蚀，在底圈壁板产生严重的腐蚀。底圈壁板承受着较大的静水压力，随着壁板的腐蚀减薄，底圈壁板的安全直接威胁着整个储罐的安全，对底圈壁板的可靠性研究十分必要。许多学者对储罐的可靠性进行了研究［1-3］，但鲜见对储罐服役过程中实时可靠性的分析。实时可靠性的分析方法主要有回归分析法［4-5］和时间序列法［6-7］，回归分析法能较好地反映各影响因素的因果关系，但模型建立需要大量的历史数据。时间序列法具有较好的拟合效果，对短期预测具有一定优势。灰色理论以小样本、不确定性系统作为研究对象，通过对已知信息的挖掘、整理来寻求系统演化的规律。针对底圈罐壁腐蚀的复杂性且检测数据较少的特点，笔者利用灰色理论建立腐蚀损伤的时变模型，并对储罐历年实测数据进行统计分析，建立储罐底圈壁板失效的概率模型，对储罐底圈壁板的时变可靠性进行分析。

1 结构抗力随机过程模型

1.1 结构抗力的衰减模型

底部罐壁长期遭受腐蚀介质的侵蚀，致使罐壁逐渐减薄，导致结构抗力随时间的增长而减弱，底圈壁板的结构抗力可表示为

式中，R(t)为t时刻罐壁的抗力，Pa;σs为罐壁的屈服强度，MPa;δ(t)为t时刻罐壁的厚度，mm;δ0为罐壁的公称厚度，mm;h(t)为罐壁腐蚀深度，mm。

通过对设计资料的分析可知，σs与δ0服从正态分布，一般h(t)服从正态分布，可表示为

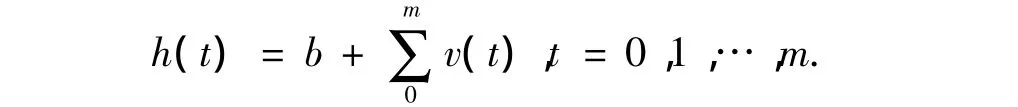
式中，b为检测时罐壁已腐蚀的深度，mm;v(t)为罐壁的腐蚀速率，mm/a;t为在服役的时间，a;m为剩余服役的时间。

腐蚀深度h(t)的平均值μh(t)和标准差σh(t)分别为

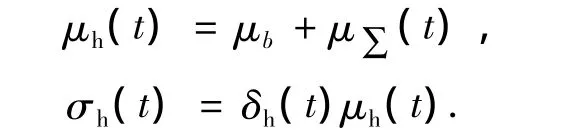
式中，δh(t)为变异系数。

1.2 底圈罐壁腐蚀速率的确定

因罐壁壁厚检测的数据较少，储罐的腐蚀机制复杂，影响腐蚀速率的因素较多，所以难以准确掌握罐壁的腐蚀规律。将灰色系统理论引入到罐壁的可靠性评估中。

罐壁腐蚀速率的求解步骤为［8］

(1)求平均时间间隔

(2)求各时段与平均时段的单位时段差系数

(3)求各时段总的差值

(4)计算等间距的灰数值

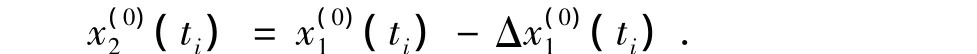
式中，μ和a为待定参数。

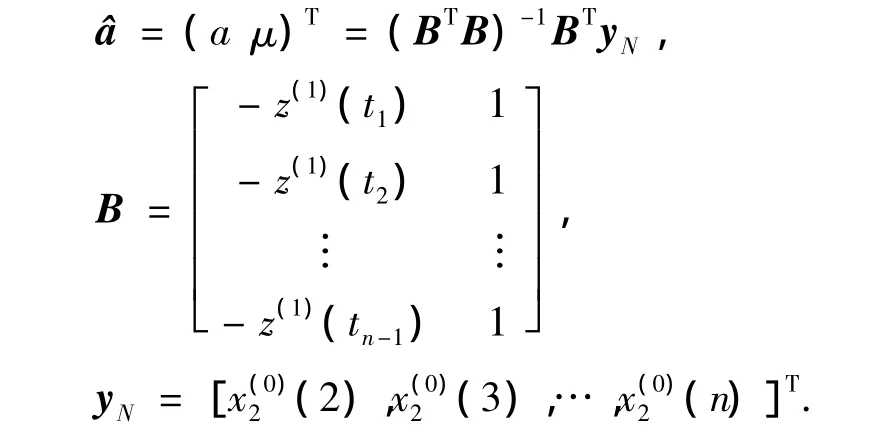
式中，z(1)(ti)为(t)在区间［ti，ti+1］上的背景值。

为提高拟合精度，学者提出了许多改进的方法，分别对预测控制的模型、模型的背景值和模型的初始值进行了优化研究［9-11］，但计算较复杂;谭冠军［12］对背景值构造方法进行研究，本文采用文献［12］的计算方法:

等分数n的经验公式为

式中，N为序列长度。

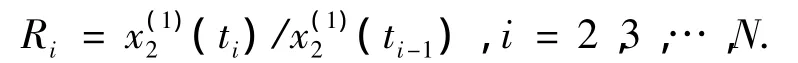
变换非等间距序列中与时间t有关的函数

得到底圈罐壁的腐蚀速率，即

2 罐壁载荷模型

罐壁的载荷主要为罐内液体的静压力和液面上较低的剩余压力，液体静压力由上至下逐渐增大，罐体液体由3部分组成:原油、油水混合液及水。联合站一般测量的数据是油的高度及油水混合液的高度，将油水混合液归入水中。如果只考虑液体压力产生的环向应力，则最大环向应力位于每圈的最下端，但由于上下圈板连接处因变截面而产生的弯矩和剪力将使各圈罐壁下端的环向力减少，因而各圈环向应力的最大值不在最下端，而在离圈板下端以上300 mm处。在底圈壁板最大环向应力处截取一微小的单元体，进行受力分析，根据静力学条件，不计该处的边缘应力，按薄膜理论，可得到环向内压力为

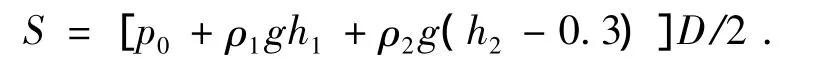
式中，p0为液面处的剩余压力，Pa;ρ1、ρ2分别为油、水的密度，kg/m3;g为重力加速度，N/kg;h1、h2分别为罐内油、水的高度，m;D为底圈罐壁的内径，m。

ρ1和 ρ2的值可以作为常量处理，p0、D、h1和 h2服从正态分布，其均值和方差可由实际数据的统计分析得知。由于罐内总的液体高度一般不会发生变化，一般为溢流口的高度，油的高度与水的高度的相关系数ρh1h2为

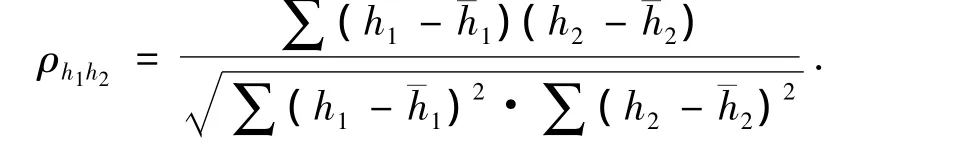
3 时变可靠度的计算

3.1 时变可靠度的模型

结构的时变可靠性定义为在规定的服役时间内，在正常设计、使用和维护下，考虑环境及结构抗力衰减等因素的影响，结构在服役某一时间后继续服役能完成预定功能的能力。设储罐在设计周期内服役t时间后，其结构抗力为R(t)，载荷为S(t)，则底圈壁板的安全裕度为

Z＞0表示结构处于可靠状态，Z＜0表示结构处于失效状态，Z=0表示结构处于极限状态。故底圈壁板的可靠度可表示为

式中，fZ(z)为Z的概率密度函数;β为可靠性指标。

3.2 可靠性指标的广义随机空间验算点法

笛卡尔坐标系的各坐标轴之间是正交的，如果建立的坐标系坐标轴之间不是正交，则称这种坐标系为广义空间［13］。在广义空间中的量称为随机变量，随机变量构成的空间称为广义随机空间。设随机变量X1，X2，…，Xn构成一n维广义随机空间，若Xi与Xj(i≠j)的相关系数为ρXiXj，则广义随机空间内各坐标轴之间的夹角为

设广义随机空间内结构的极限功能函数为

再设x*=()T为极限状态面上的一点，即 gX(x*)=0，在点 x*处将式(5)按Taylor级数展开并取至一次项，有

方程ZL=0为过点x*处的极限状态面的切平面。在广义随机空间中，可靠度指标β为标准正态随机变量坐标系的原点到极限状态面的最短距离，验算点p*就是与此距离对应的极限状态面上的点。由相关正态随机变量的性质，结构可靠指标为

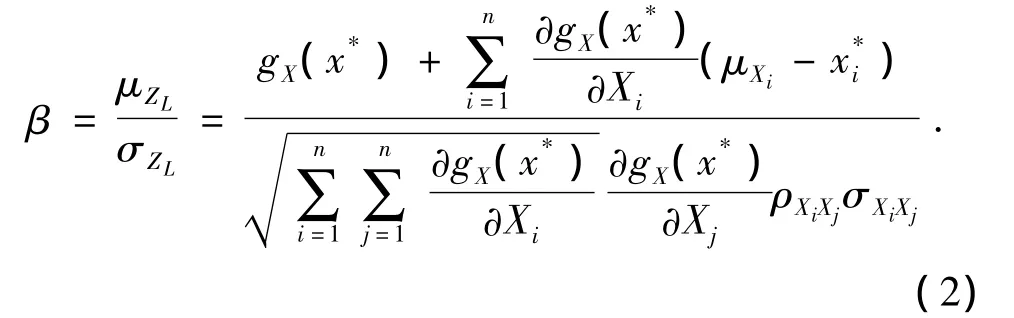
定义变量Xi的灵敏度系数为

设计验算点p*在原始X空间中的坐标为

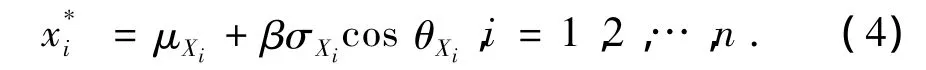
式(2)～(4)组成了广义随机空间内迭代求解可靠度指标β的公式。

4 实例分析

胜利油田某联合站1号罐为沉降罐，1992年投入使用，公称容积为5 000 m3，内径为23.7 m，罐高为13.54 m，溢流高度为12.1 m，底圈壁板的初始厚度为14 mm，罐壁材料为Q235A。

根据检查中心测量的数据，底圈壁板的厚度测量值如表1所示，将其进行统计分析，频率直方图与正态概率图如图1所示，正态概率呈直线分布，并经假设检验得知腐蚀深度符合正态分布。

表1 底圈壁厚测量值Table 1 Measured values of bottom shell thickness mm

图1 底圈壁板腐蚀深度的统计分析Fig.1 Statistical analysis of corrosion depth of tank bottom shell

将储罐一个月的油、水高度值进行统计分析，其正态概率如图2所示。由图2可以看出，它们基本上呈直线分布;根据K－S检验的计算公式［14］，计算出D分别为0.102 0和0.099 3，显著性水平a=0.05的临界值为0.245 71，显然0.102 0与0.099 3都小于0.24571，可认为油高与水高符合正态分布。计算出油高的均值和标准差分别为2.603 m、0.495，水高的均值和标准差分别为 9.498 m、0.490，可计算出相关系数ρh1h2=－0.9973。储罐的其他基本变量特征如表2所示。

在服役时间分别为13、15、16、19、22 a 时，平均腐蚀速率 v分别为 0.130 6、0.135 3、0.137 3、0.141 4、0.1500 mm·a－1。计算可得

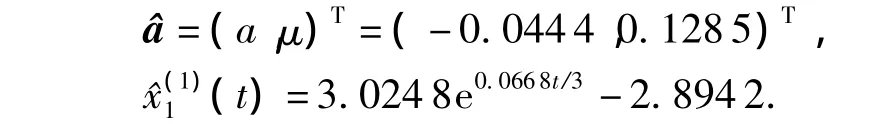
根据灰色理论预测精度的检验方法及精度等级［8］，可计算出 C=0.228 6，P=1，一般要求 C ＜0.35，最大不超过0.65，P ＞0.95，不得小于 0.7，如果C较小且P较大，则该预测的精度就高。根据此精度检验的等级可以看出，底圈壁板的腐蚀速率预测精度较高。

图2 油高与水高的正态概率图Fig.2 Normal probability plot of oil height and water height

根据表2中的数据及腐蚀速率，由式(2)～(4)进行迭代计算，可得到可靠性指标及可靠度如表3和图3所示。由图3可以看出，该储罐底圈壁板的可靠性指标和可靠度随时间的增长而降低。API579［17］中规定在役设备结构目标失效概率一般为10－3，根据此规定储罐在服役22 a后其失效概率超过10－3，应对罐进行适当的维修与维护。

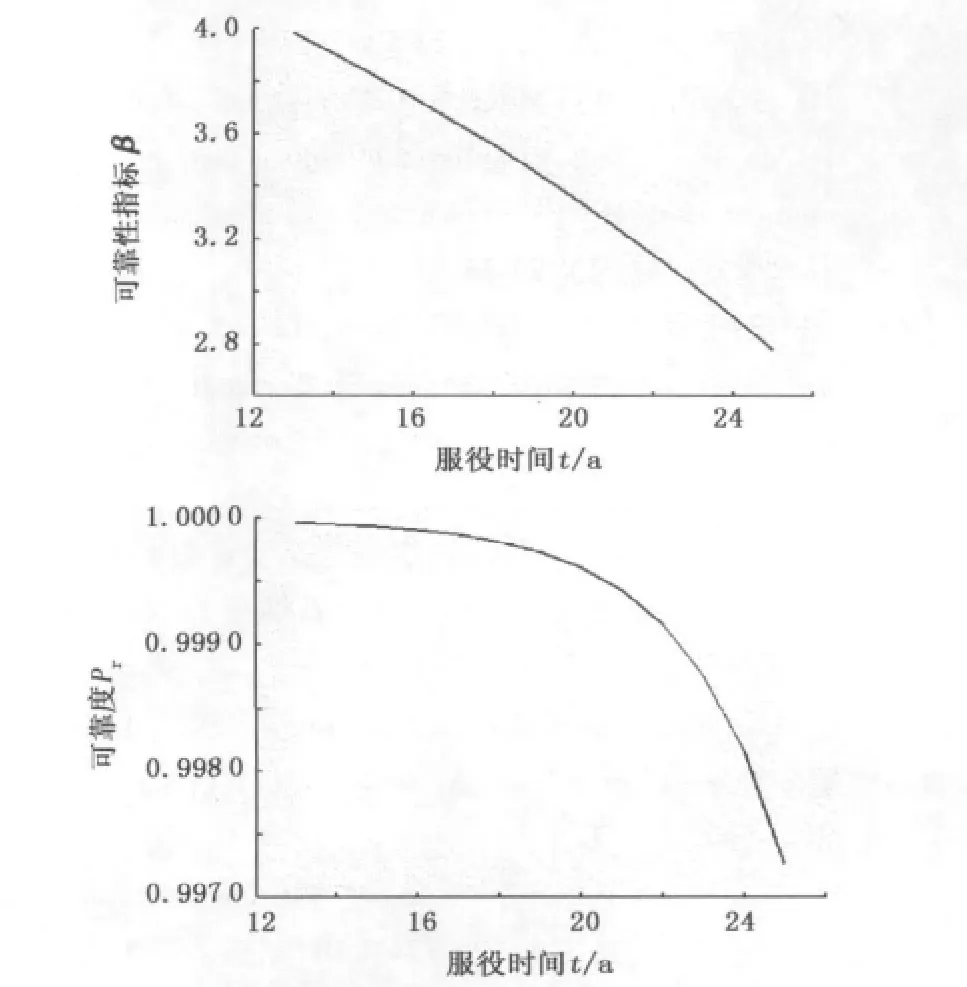
图3 可靠性指标及可靠度随时间变化规律Fig.3 Change law of reliability indices and reliability with time

5 结论

(1)底圈壁板的腐蚀深度和罐内油、水的高度符合正态分布。

(2)储罐壁厚的测量数据较少且各检测时间不等，可利用灰色系统理论建立预测模型，且拟合精度较高。

(3)可靠性指标和可靠度随时间的增长而降低，储罐在服役22 a后应对储罐进行适当的维修与维护，可为储罐的维修维护提供决策支持。

［1］ 唐勇，贺小华.基于有限元的罐体可靠性分析和设计［J］.化工机械，2011，38(5):546-549.TANG Yong，HE Xiao-hua.Reliability analysis and design of spherical tank based on FEM method［J］.Chemical Engineering ＆ Machinery，2011，38(5):546-549.

［2］ 屈渭，郭建科，黄海波，等.在役立式钢制油罐底圈罐壁可靠性分析［J］.后勤工程学院学报，2005，21(2):43-46.QU Wei，Guo Jian-ke，HUANG Hai-bo，el al.Reliability analysis applied to the bottom shell of the vertical steel oil tanks in service［J］.Journal of Logistical Engineering University，2005，21(2):43-46.

［3］ 胡宗柳，吴明，刘勇峰，等.基于有限元法的球罐强度可靠性分析［J］.辽宁石油化工大学学报，2011，31(4):26-28.HU Zong-liu，WU Ming，LIU Yong-feng，et al.Strength reliability analysis of spherical tanks based on the finite element method［J］.Journal of Liaoning Shihua University，2011，31(4):26-28.

［4］ GEBRAEEL N Z，LAELEY M A，LI R，el al.Residual life distributions from component degradation signals:a Bayesian approach ［J］.IEEE Transactions，2005，37(6):543-557.

［5］ 陈团海，陈国明，许亮斌.基于台风验证载荷的平台时变可靠性分析与更新［J］.中国石油大学学报:自然科学版，2011，35(3):129-134，139.CHEN Tuan-hai， CHEN Guo-ming， XU Liang-bin.Time-dependent reliability analysis and updating of offshore platforms based on typhoon proof load［J］.Journal of China University of Petroleum(Edition of Natural Science)，2011，35(3):129-134，139.

［6］ LU H，KOLARIK W J，LU S S.Real-time performance reliability prediction［J］.IEEE Trans Reliab，2001，50(4):353-357.

［7］ 尤琦，赵宇，胡广平，等.基于时序模型的加速退化数据可靠性评估［J］.系统工程理论与实践，2011，31(2):328-332.YOU Qi，ZHAO Yu，HU Guang-ping，et al.Reliability assessment using accelerated degradation data based on time series model［J］.Systems Engineering-Therogy ＆Practice，2011，31(2):328-332.

［8］ 袁嘉祖.灰色系统理论及其应用［M］.北京:科学出版社，1991:126-136.

［9］ 戴文战，李俊峰.非等间距GM(1，1)模型建模研究［J］.系统工程理论与实践，2005，25(9):89-93.DAI Wen-zhan，LI Jun-feng.Modeling research on nonequidistance GM(1，1)model［J］.Systems Engineering-Therogy ＆ Practice，2005，25(9):89-93.

［10］ 王晓佳，杨善林.基于组合插值的GM(1，1)模型预测方法的改进与应用［J］.中国管理科学，2012，20(2):129-134.WANG Xiao-jia，YANG Shan-lin.The improvements and applications of forecasting method in GM(1，1)model based on combinative interpolation［J］.Chinese Journal of Management Science，2012，20(2):129-134.

［11］ GAO Cai-yun，GAO Ning.A new kind of optimized method of grey prediction model and its applications in deformation［C］//IEEE Computer Society.Proceedings-2009 International Conference on Information Engineering and Computer Science.United States:c2009.

［12］ 谭冠军.GM(1，1)模型的背景值构造方法和应用(Ⅰ)［J］.系统工程理论与实践，2000，20(4):98-103.TAN Guan-jun.The structure method and application of background value in grey system GM(1，1)model(Ⅰ)［J］.Systems Engineering-Therogy ＆ Practice，2000，20(4):98-103.

［13］ 赵国藩，金伟良，贡金鑫.结构可靠度理论［M］.北京:中国建筑工业出版社，2000:79-98.

［14］ 吴喜之，王兆军.非参数统计方法［M］.北京:高等教育出版社，1996:144-146.

［15］ GB 50128-2005立式圆筒形钢制焊接储罐施工及验收规范［S］.北京:中国计划出版社，2006.

［16］ 帅建，于桂杰.管道及储罐强度设计［M］.北京:石油工业出版社，2006:179.

［17］ API RP 579.2000 Recommended practice for fitnessfor-service［S］.Washington:American Petroleum Institute，2001.