气体钻井井底岩石热应力分析

仉洪云，高德利，郭柏云

(中国石油大学石油工程教育部重点实验室，北京 102249)

钻井过程中，温度的影响研究主要集中在井筒流体和地层传热方面［1-3］，也有研究井壁围岩温度变化引起的热应力对井壁周围应力分布的改变［4-6］，气体自钻头喷嘴喷出后发生焦耳－汤姆逊冷却效应，井底低温气体与地层岩石发生热传导，由于岩石变形受到限制而产生的热应力并没有引起足够的重视。目前用试验方法研究井底应力场比较困难，主要通过数值方法［7-8］，且很少涉及到热应力。笔者从理论分析角度考虑井底焦耳－汤姆逊冷却效应，建立井底岩石稳态温度和热应力分布模型，并与井底岩石非稳态温度和热应力分布模型进行对比，分析低温效应对井底岩石热应力分布的影响。

1 数学模型

1.1 井底温度

钻井过程中，气体通过钻杆从钻头喷嘴喷出的过程可视为渐缩喷嘴流动，对于不同的钻井流体可能产生超声速、声速、亚声速流动。声速流是否存在取决于喷嘴下游与上游压力比，如果这个比值小于临界压力比就会产生声速或超声速流动，大于临界压力比时会产生亚声速流动。由于在声速或者超声速条件下，喷嘴处存在压力间断，容易出现井下事故，并且气体钻井中钻井流体主要用来清洗井底、携带岩屑，因此在气体钻井过程中一般要保持亚声速流动。

井底温度受井口注入温度、地温梯度、井深、钻井液的热学性质等多种因素的影响。在气体钻井中井底温度比地层温度低很多，因为在钻头喷嘴处发生了焦耳－汤姆逊冷却效应，气体通过钻头喷嘴后产生压力损失，体积突然膨胀导致气体温度下降。假设通过钻头喷嘴是一个理想气体等熵流动过程，气体以声速、亚声速通过钻头喷嘴时，喷嘴下游温度［9］为

式中，Tup和Tdn分别为钻头上、下游温度，K;pup和pdn分别为钻头上、下游压力，N/m2;k为绝热指数。

气体以声速通过钻头喷嘴，钻头下游气体的绝对温度约下降17%。上游温度为54℃时，钻头下游温度达到0℃，如果地层中有水，就会出现“冰包”。当钻头上下游压力比大于临界压力比，气体以亚声速通过钻头喷嘴，上游温度为52℃ 时，钻头下游温度达到0℃。当气体亚声速通过钻头时，钻头上下游压力比越大，上游温度越低，钻头下游温度越容易达到0℃。亚声速流动比声速流动更容易使得钻头下游温度达到0℃，也就是出现“冰包”、“泥包”钻头的可能性要大些。气体钻井过程中应该控制井底温度，降低出现井下事故的可能。

当钻头处于某一深度时，钻头上游的温度可能比地层温度低，气体经过钻头喷嘴后的温度要低于钻头上游温度，低温气体携岩上返对钻头又是一个冷却降温的过程。井底岩石温度高于井底温度，会在井底附近产生较高的温度梯度。

1.2 井底岩石热应力模型

1.2.1 稳态井底岩石热应力

计算井底岩石热应力首先应该确定井底岩石温度分布。经过焦耳-汤姆逊冷却效应产生的低温气体作用在井底，与井底岩石之间存在热量传递，井底岩石温度仅沿半径方向变化。

假设:地层岩石导热系数为常量;地层岩石初始时刻温度和无穷远处温度均匀，为原始地温，并且地层内无内热源产生热量;导热过程开始时井底壁面温度保持恒定。

井底岩石的温度分布模型见图1。井底岩石温度分布可用球坐标系下的岩石温度T、半径r表示。

图1 井底岩石温度分析模型Fig.1 Analysis model of bottom hole rock temperature井底岩石温度分布为

整理式(2)并积分得

设井底温度为Tf，初始地层温度为T0，则当r=a 时，T=Tf;当 r=b时，T=T0，其中 b为某时刻温度影响到的球坐标半径，m;a为井眼半径，m。将该边界条件代入式(3)，可以求出A、B表达式为

将A、B表达式代入式(3)，得到井底岩石温度分布的表达式为

基于井底温度分布的假设，球体中的温度场沿半径方向变化，产生球对称温度场。采用热弹性理论的方法可得井底岩石热应力表达式为

当b→∞ 时，整理后得

式中，β为热膨胀系数，℃－1;E为弹性模量，MPa;ν为地层泊松比。

1.2.2 非稳态井底岩石热应力

考虑时间对井底岩石温度分布的影响，井底岩石温度随井底壁面温度作用时间和径向距离变化。在一定时间限度内，边界面处的温度影响深度有限，在这个深度以外，地层仍保持原有状态。井底壁面与井底岩石的热量传递简化为一维非稳态导热问题来处理，可以得到井底岩石温度分布模型［10］为

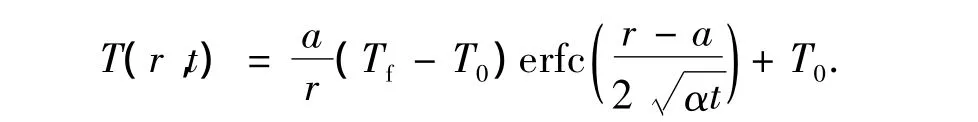
其中

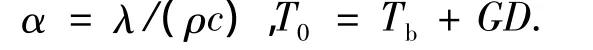
式中，λ为导热系数，W/(m·℃);α为导温系数，m2/s;Tb为地表温度，℃;G为地温梯度，℃/m;D为井深，m;t为时间。

参照稳态热应力求解方法得到的非稳态井底岩石热应力为

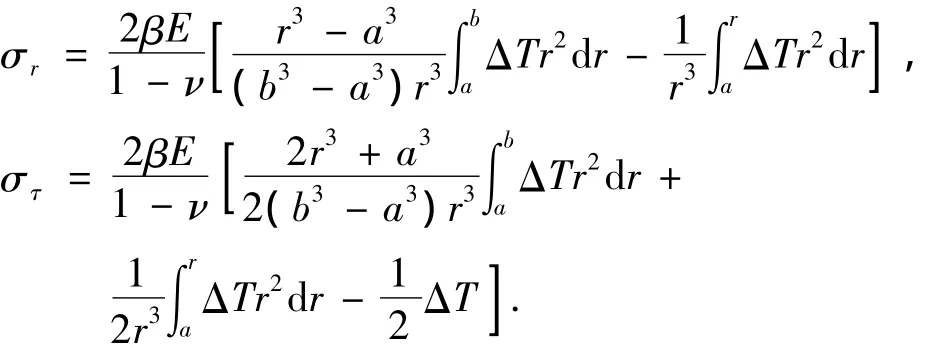
当b→∞时，

式中，ΔT为某一时刻地层温度与初始地层温度之差，℃。

2 算例分析

某气藏井深3.0 km，井眼直径0.216 m，地层岩石密度2.52 g/cm3，比热容为0.82 J/(g·℃)，热传导系数3.42 W/(m·℃)，地温梯度0.03℃/m，地表温度20℃，地层泊松比0.251，弹性模量34.7 GPa，热膨胀系数 1 × 10－4℃－1。

温度模型采用球坐标，选取井眼径向距离分析井底岩石温度变化(图2)。由图2可以看出:稳态井底岩石温度随着径向距离增大逐渐升高，而后逐渐接近初始地层温度，表明由于井底低温气体和地层岩石发生热传导，井底附近岩石在一定范围内存在低温区，形成了由井底到无限远处温度逐渐升高直至达到地层初始温度的分布曲线;非稳态井底岩石温度分布受时间的影响尤为明显，随时间的增加低温影响范围扩大，逐渐影响到离井底较远的岩石温度。

图2 井底岩石温度分布Fig.2 Temperature distribution of bottom hole rock

由于岩石热传导系数很小，井底附近岩石存在很大的温度梯度，在井眼径向距离很小的范围内迅速达到初始地层温度。井底附近岩石温度变化用初始地层温度与某一时刻地层温度差来描述，如表1所示。

气体钻井中钻头敲击旋转钻进，钻头下方处于压缩状态的岩石破碎，在焦耳－汤姆逊冷却效应作用下井底温度低于地层岩石温度，在温差作用下发生热传导后井底附近岩石温度降低，从而地层岩石温度低于远离井底的地层岩石温度。由于上覆岩层被打开，井底壁面岩石变形不受限制，无径向热应力产生。井底附近岩石温度降低后较之没有发生热传导之前产生收缩，井底岩石初始的压缩状态发生变化，地层在负压差条件下产生向井内的“拉应力”，使得地层岩石变形受到限制，产生热应力。

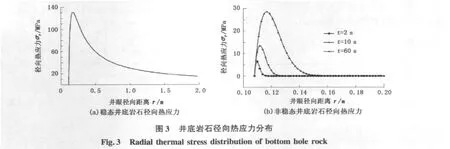
图3为稳态和非稳态情况下井底岩石径向热应力分布。井底岩石受到的径向热应力随井底距离的增加而增大，达到最大值后随着径向距离增大而逐渐减小，存在一个峰值。由图2可以看到t=2 s时，在井底径向距离0.11 m处温度已经降为原始地层温度，图3中井底径向距离0.11 m处径向热应力也下降到零，说明温差对井底岩石热应力的影响显著。当钻头钻速10 m/s、t=2 s时，钻进深度0.005 m，径向热应力数值最大处距离井底0.002 m，说明钻头钻进过程中会钻遇径向热应力最大处，对于钻头破岩有利。

表1 井底岩石温差计算值Table 1 Computing value of bottom hole rock temperature difference

气体钻井过程中，井底压力变小，随着钻头钻进，地层岩石应力状态发生改变。井底岩石从初始的压缩状态变为在很大负压差条件下产生向井内的拉伸状态，由于岩石抗拉强度低于抗压强度，使得这个拉应力有促使井底岩石脱离井底的趋势。气体钻井压持作用很小，岩石被打开后硬度会大大降低。井底由于温度变化产生的径向热应力在井底沿径向存在拉应力，与由于负压差产生的“拉应力”叠加之后加强了井底岩石向井眼变形的趋势，促进井底岩石破裂。

图4为井底岩石切向热应力分布。从图4可以看出，井底壁面处切向热应力最大，随着距井底距离的增加切向热应力减小，直到减小为零，非稳态切向热应力减小速度快于稳态切向热应力，由于不考虑时间的影响，稳态切向热应力曲线趋势较为平缓，影响范围也较大。切向热应力最大值超过400 MPa，而一般岩石抗压强度小于350 MPa，因此不能忽视切向热应力对岩石破裂的影响。

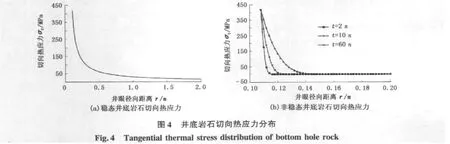
由于井底壁面处不存在径向热应力，切向热应力最大，观察井底温度与井底岩石切向热应力之间关系可以看到，随着井底气体温度降低，在井底壁面处的切向热应力增大。气体钻井中随着井底压力降低，井底岩石沿井底方向上产生膨胀变形，从而出现微裂纹［12］。钻头对井底岩石进行敲击，使得岩石裂纹进一步扩大延伸，牙齿吃入岩石进行旋转，岩石产生炸裂。井底由于温度变化产生的切向热应力数值很大，并且在井底壁面处最大，有利于岩石剪切破碎。与井底岩石受到的地应力叠加之后增大井底岩石受到的地应力作用，很大程度上促进了钻头破岩，提高了气体钻井机械钻速。

3 结论

(1)井底低温气体和地层岩石发生热传导，使得井底附近岩石存在很大的温度梯度，在一定范围内存在低温区。岩石热传导系数较小，在较短的时间内井底低温影响范围很小，随着时间延长低温影响范围逐渐扩大。

(2)井底岩石由于温度变化产生的径向热应力在井底沿径向形成拉应力，与由负压差产生的“拉应力”叠加后加大了井底岩石向井眼变形的趋势，促进了井底岩石破裂。切向应力在井底壁面处最大，且数值较大，有利于剪切破碎，因此在判断岩石破裂时应考虑热应力的影响。

(3)井底岩石热应力随着井底气体温度降低而增大，保持适当的井底温度有利于井底岩石破裂，提高机械钻速。

(4)时间对于井底岩石热应力的影响较大，在研究井底低温问题时不可忽略时间因素的影响。

［1］ RAMEY H J.Wellbore heat transmission［R］.SPE 96，1962.

［2］ WILLHITE G P.Over-all heat transfer coefficients in stream and hot water injection wells［R］.SPE 1449，1967.

［3］ ROMERO J.Temperature prediction for deep-water wells:a field validated methodology［R］.SPE 49056，1998.

［4］ DUSSEAULT M B.Stress changes in thermal operations［R］.SPE 25809，1993.

［5］ VINCENT M，IDELOVICI J L.Safe drilling of HP/HT wells，the role of the thermal regime in loss and gain phenomenon［R］.SPE/IADC 29428，1995.

［6］ 蔚宝华，卢晓峰，王炳印，等.高温井地层温度变化对井壁稳定性影响规律研究［J］.钻井液与完井液，2004，24(6):15-18.WEI Bao-hua，LU Xiao-feng，WANG Bing-yin，et al.Law of temperature influence on wellbore stability in hot well［J］.Drilling Fluid ＆ Completion Fluid，2004，24(6):15-18.

［7］ 彭烨，沈忠厚，樊胜华，等.基于开挖方法的井底应力场有限元模型［J］.石油学报，2006，27(6):133-140.PENG Ye，SHEN Zhong-hou，FAN Sheng-hua，et al.Finite element model for analyzing stress field of bottom hole based on excavating method［J］.Acta Petrolei Sinica，2006，27(6):133-140.

［8］ 王敏生，唐波.井底应力场对气体钻井井斜的影响［J］.岩体力学，2009，30(8):2436-2441.WANG Min-sheng，TANG Bo.Effects of stress field in bottom hole on borehole deviation during gas drilling［J］.Rock and Soil Mechanics，2009，30(8):2436-2441.

［9］ LYONS William C，GUO Boyun，SEIDEL Frank A.空气和气体钻井手册［M］.曾义金，樊洪海，译.北京:中国石化出版社，2006.

［10］ ZHANG Hui，ZHANG Hongyun，GUO Boyun，et al.Analytical and numerical modeling reveals the mechanism of rock failure in gas UBD［J］.Journal of Natural Gas Science and Engineering，2012(4):29-34.

［11］ 楼一珊，金业权.岩石力学与石油工程［M］.北京:中国石化出版社，2006.

［12］ 刘永贵，王洪英.徐深气田气体钻井破岩机理的初步研究［J］.石油学报，2008，29(5):773-776.LIU Yong-gui，WANG Hong-ying.Initial research on rock-breaking mechanism for gas drilling in Xushen Gas Field［J］.Acta Petrolei Sinica，2008，29(5):773-776.