某水电站库区变形体滑坡涌浪初步分析

2013-10-23谷健

水电站设计 2013年4期

谷健

(中国水电顾问集团成都勘测设计研究院，四川成都 610072)

1 前言

理论界对于滑坡涌浪的理论预测方法研究主要基于两个方面:一种是从流体力学出发，通过物理力学定律导出数学模型;一种是通过常数与函数的量纲分析和经验归纳得出合适的理论公式。主要方法有潘家铮算法、北京水电科研院算法、诺达(Noda．E)方法、凯姆夫斯和包尔荣(Kamphis，J．W and Bowering，R．J方法 1972)、R．L．Slingerland and B．volght方法(1972)、瑞士方法(1982)、模型试验法等［1］。本文采用较常用的潘家铮法对某水电站库区变形体滑坡涌浪进行分析计算。

2 库区变形体概况

该水电站系四川省境内雅砻江干流上的一个梯级电站。水库正常蓄水位1 330m，死水位1 328m，总库容7.6亿m3，回水长约58km，为日调节水库。电站枢纽主要由拦河碾压混凝土重力坝、泄洪消能建筑物、引水发电建筑物等组成，最大坝高168m。工程于2011年11月初开始下闸蓄水，2012年2月15日发现距坝址河道距离约17km的库岸边坡发生变形。

初步查勘表明，该岸坡一带为古变形体，主要为玄武岩碎石土组成，前缘沿河长约1.9km，后缘最高高程约为2 070m，平面面积约1.6km2。河床枯水期水位1 235m，最大拨河高差约835m，距正常蓄水位的最大高差约740m，正常蓄水位水深约93m。2月15日，大坝蓄水至1 282m，变形体前缘出现变形复活现象。

3 涌浪分析计算

3.1 潘家铮算法

潘家铮利用单向流分析成果，再根据一些近似假定，提出了涌浪高程的近似估算法，来分析较为复杂的水库涌浪问题。近似估算法假定［2］:

(1)涌浪首先在滑坡入水处发生，产生初始波，然后向周围传播。在传播过程中，不断变形，但忽略能量损耗，或假定损耗为已知。

(2)忽略边界条件的非线性影响，假定全部涌浪过程可以视为在一系列源点处产生的小波影响的线性迭加。所以对于水深较浅的水库，计算误差可能较大。

(3)每个小波成分都是孤立波，以涌浪形式在水面上传播。波速c为常数。

(4)假定涌浪到达库岸后发生全反射，或其反射系数k为已知值。

变形体失稳破坏时假定为一次同时滑下，为垂直变形的情况。具体公式如下:

(1)滑坡体水库对岸最高涌浪按下式计算:

历时T及涌浪从本岸传播到对岸需时Δt=B/c。如果L/B不太大，级数中采用的项数如下所示:

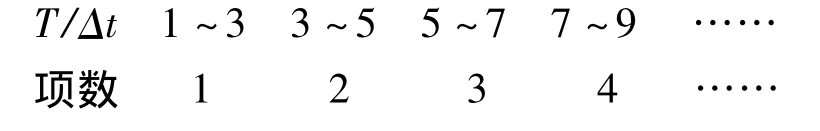
波速c可按下式计算:

(2)水库大坝处最高涌浪按下式计算:

可以这样计算:设河道宽为B，滑坡区中心到大坝的水平距离为x，则:

3.2 边界条件

变形体后缘位于高程1 537m，前缘剪出口位于岸边高程1 258m附近，变形体范围厚度为0～190m。选用正常蓄水位1 330m时变形体失稳破坏后形成的涌浪进行计算分析。

3.3 参数选取

水电站库区变形体处水库库面宽340m，水深93m。现无法确定变形体下滑时的范围和厚度，故选取了两种下滑可能进行计算分析:当Ⅲ区整体下滑时，滑坡体长210m，滑坡体平均厚度20m，估计方量100万m3左右;当Ⅳ区整体下滑时，滑坡体长480m，滑坡体平均厚度95m，估计方量1 000万m3左右，若平均厚度取50m，估计方量500万m3左右。滑动速度分别取 5m/s、10m/s、15m/s 和 20m/s，该变形体距大坝17km，选取距大坝不同距离进行分析计算。

3.4 计算成果

(1)当Ⅲ区整体下滑时。利用前述的潘家铮法计算出了在不同滑动速度、不同滑动历时下的初始涌浪高度和对岸最高涌浪高度。滑动历时分别选取了10s、15s、20s和25s四种工况。计算结果见表1和图1。

在不同滑速下，不同距离的涌浪高度不同，计算结果见表2和图2。

(2)当Ⅳ区整体下滑时。当滑坡体平均厚度为95m，估计方量为1 000万m3左右时，同样可以得到变形体在不同滑速和不同滑动历时下对岸最高涌浪高度，见表3、图3。

表1 变形体在不同滑速和不同滑动历时下对岸最高涌浪高度

图1 不同滑速下初始涌浪高度与对岸最高涌浪高度的对比关系

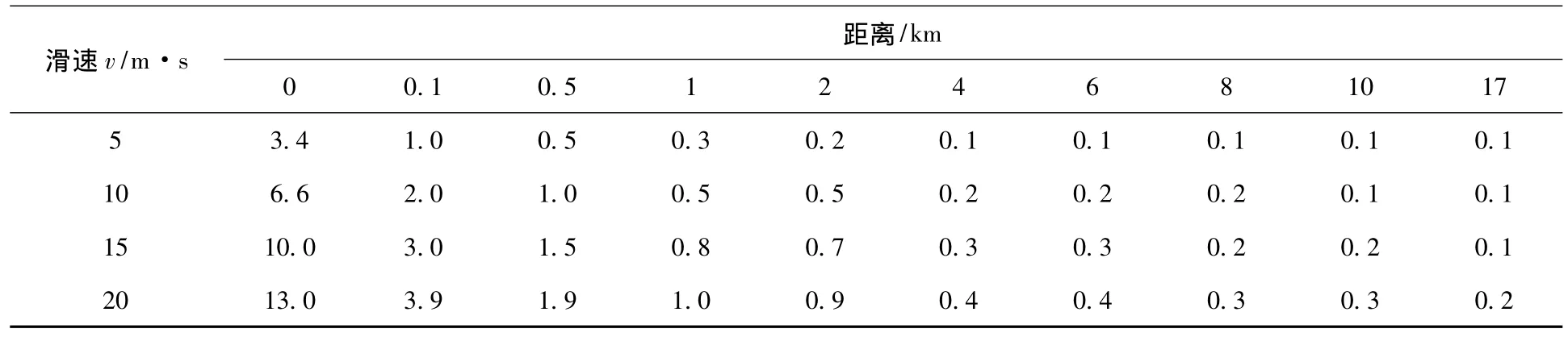
表2 不同距离时在不同滑速下的涌浪高度(滑动历时T=10s时) m

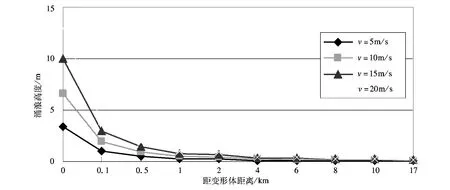
图2 不同滑速下涌浪高度与距变形体距离的关系

表3 变形体在不同滑动速度、不同滑动历时下的初始涌浪高度和对岸最高涌浪高度

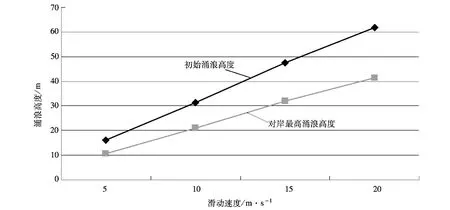
图3 不同滑速下初始涌浪高度与对岸最高涌浪高度的对比关系

另外，距变形体失稳破坏后形成涌浪的距离远近，在不同的滑速下，涌浪高度差异很大，计算结果见表4和图4。

当滑坡体平均厚度为50m，估计方量500万m3左右时，计算结果见表5、图5。

另外，距变形体失稳破坏后形成涌浪的距离远近，在不同的滑速下，涌浪高度差异很大，计算结果见表6。可以用图6清晰的展现出来。

3.5 成果分析

(1)涌浪高度在不同的滑动速度和不同变形体规模下是不同的。涌浪高度随滑动速度的增大和变形体规模的增大而增大。

(2)在变形体规模大小即方量不同时，对岸最高涌浪高度有所不同。当III区下滑(100万m3左右)时，滑动速度20m/s时对应的对岸最高涌浪高度在4.8m左右;当Ⅳ区下滑(500万m3左右)时，滑动速度20m/s时对应的对岸最高涌浪高度在24.1m左右;当Ⅳ区下滑(1 000万m3左右)时，滑动速度20m/s时对应的对岸最高涌浪高度在41.5m左右。根据潘家铮法分析计算理论，涌浪在有阻挡的情况下，其高度将有所增加。因而涌浪对对岸的影响较大。

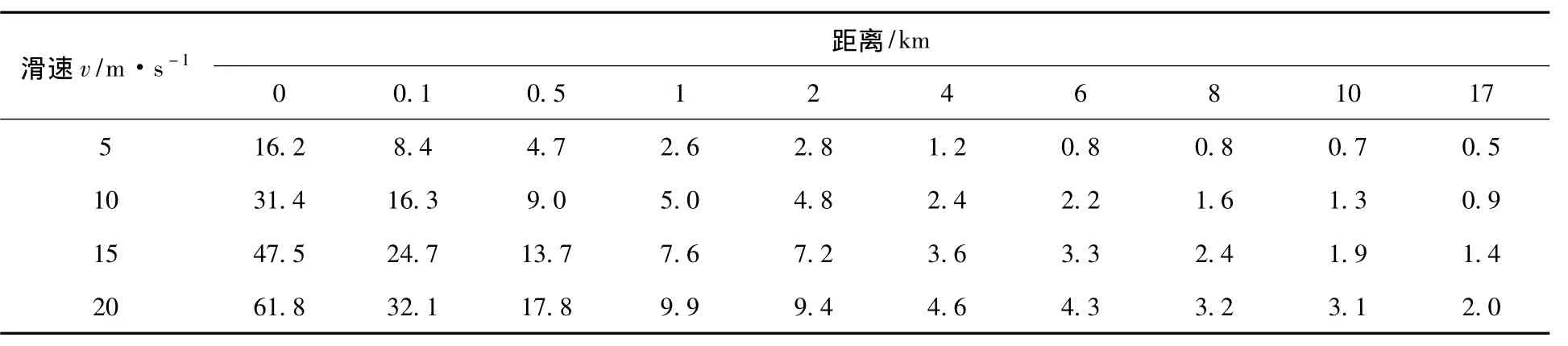
表4 不同距离时在不同滑速下的涌浪高度(滑动历时T=10s时) m

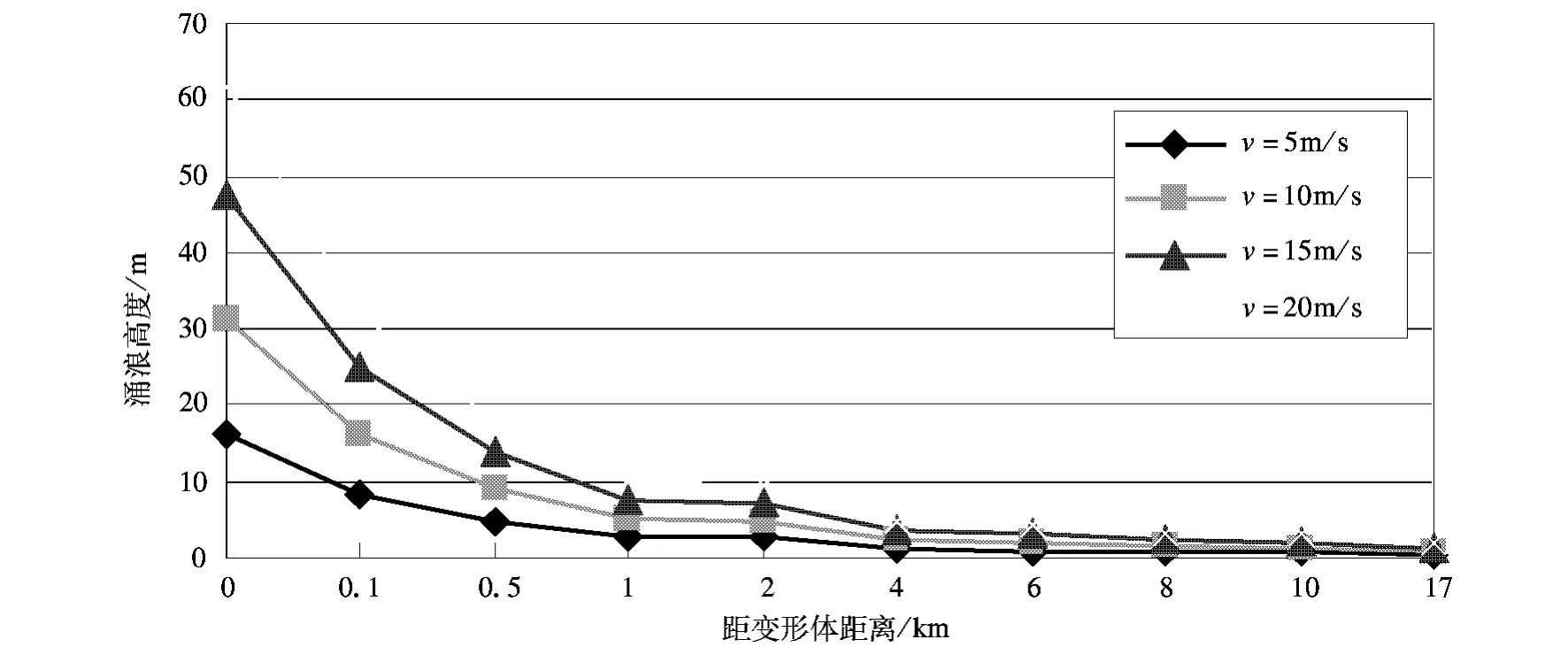
图4 不同滑速下涌浪高度与距变形体距离的关系

表5 变形体在不同滑动速度、不同滑动历时下的初始涌浪高度和对岸最高涌浪高度

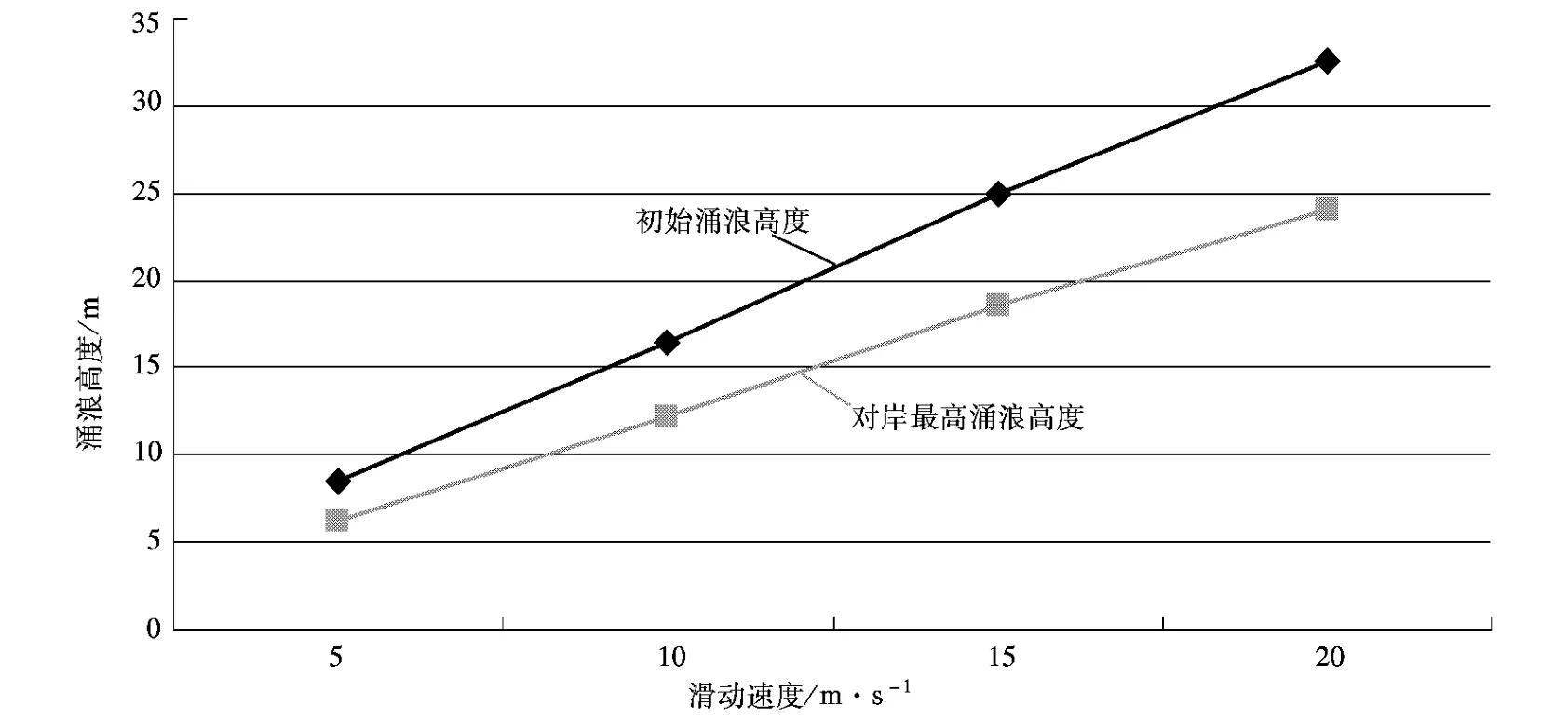
图5 不同滑速下初始涌浪高度与对岸最高涌浪高度的对比关系

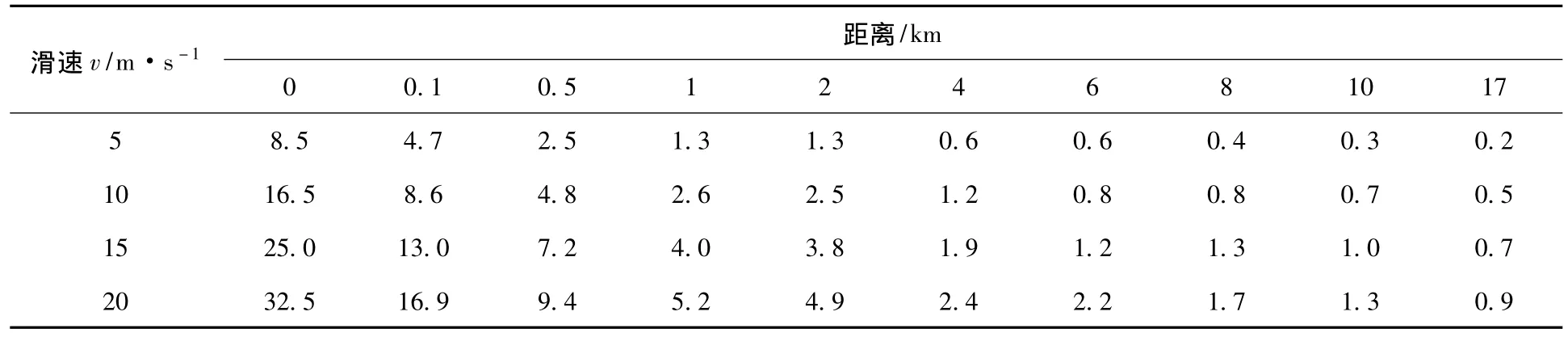
表6 不同距离时在不同滑速下的涌浪高度(滑动历时T=10s时)m

图6 不同滑速下涌浪高度与距变形体距离的关系

(3)从图2、3、4中可以清楚发现，当III区下滑时，1km处涌浪高度在0.98m以下;当Ⅳ区(500万m3左右)下滑时，1km处涌浪高度在5.2m以下;当Ⅳ区(1 000万m3左右)下滑时，1km处涌浪高度在9.9m以下。对于水库变形体失稳破坏形成的涌浪高度，在距变形体最近的1km范围内衰减得最快，1～4km范围衰减较快，4km以外涌浪已趋于平缓。

(4)在不考虑库区河谷弯道对涌浪削减作用的情况下，滑动速度20m/s时，当Ⅳ区(500万m3左右)下滑时，涌浪在距离17km远的大坝处衰减到了1.0m以下;当Ⅳ区(1 000万m3左右)下滑时，涌浪在距离17km远的大坝处衰减到了2.0m以下;仅III区下滑时已衰减到了0.2m左右。可见变形体失稳形成的涌浪对大坝安全的工程影响是有限的。