失效准则对工程估算复合材料连接强度的影响
2013-10-21李亚智
李 玺,李亚智,姜 薇,李 彪
(西北工业大学 航空学院,西安 710072)
复合材料以其优越的性能在航空和航天领域得到越来越广泛的应用.在飞机结构中,复合材料机械连接接头是重要结构部位,其力学性能、强度和寿命值得关注.复合材料机械连接强度研究方法主要有试验法、基于累积损伤的分析方法和基于特征曲线的工程估算方法.累积损伤法可以对损伤过程和失效强度进行合理的预测,但由于复合材料连接损伤机理复杂,应力分析繁复,刚度退化方式各异,这对设计人员的应用造成诸多不便.因此,为了满足工程需求,设计人员经常采用特征曲线法估算机械连接强度.特征曲线法是一种近似估算方法,它不关注结构损伤的演变过程,但是应用方便.
特征曲线法最早由Whitney和Nuismer[1]提出,后来被Chang 等人[2]应用到复合材料机械连接接头强度分析方面,根据特征曲线上的应力,以某种准则为失效判据来预测层合板机械连接的强度值.在传统方法中,特征曲线的长轴及短轴长(Rc和Rt)需要通过试验测定.Jin-Hwe Kweon 等[3]提出用数值计算确定特征长度的方法,脱离了原有的确定特征长度的试验方法,降低了成本.之后,Camanho和Lambert[4]提出用层合板中的单层而非等效层合板来确定特征长度及特征曲线,从而有理由用单层失效准则确定接头强度.赵美英等[5]提出用临界层的特征长度来确定层合板的特征曲线,再结合失效准则确定连接件强度.虽然特征曲线方法计算简单,耗费较少,但是对于不同的失效准则,特征曲线方法的计算精度不同.Aluko[6]利用试验数据确定特征曲线,再利用连接应力的解析解考察了不同失效准则的计算精度,发现几种失效准则计算结果的平均值更接近试验值.
本文根据数值计算结果确定特征曲线,在特征曲线法分析中采用不同的失效准则,进行强度预估精度对比,为合理选用失效准则提供参考.
1 特征曲线法
1.1 特征曲线的定义
特征曲线法由Whitney和Nuismer[1]提出.如图1所示,特征曲线由带孔板的拉伸和压缩特征长度所决定,其表达式为:.
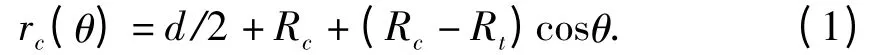
其中:Rc和Rt分别代表含孔层合板的压缩和拉伸特征长度.

图1 特征曲线
当特征曲线确定后,根据特征曲线上的应力,以某种准则作为失效判据,以特征曲线上的首个单元失效表征整个连接细节失效,以此来预测层合板机械连接强度.
1.2 压缩特征长度的确定
利用Kweon[3]提出的通过数值计算确定特征长度的方法.压缩特征长度定义为从孔边挤压前缘点沿挤压方向到某一点的距离.如图2所示,钉孔受到任意大小的挤压载荷作用时,该点处局部压缩应力等于式(2)中的平均挤压应力

其中:Pc为挤压载荷,t、d 分别代表层合板的厚度和孔径.

图2 压缩特征长度的定义
Kweon[3]指出,层合板的压缩特征长度不会随挤压载荷的不同发生变化.
1.3 拉伸特征长度的确定
拉伸特征长度定义为从孔边一侧边缘到某点的距离.如图3所示,含孔层压板在纵向任意拉伸载荷作用下,该点的局部拉伸应力等于式(3)中的平均拉伸应力:

其中:Pt表示任意大小的拉伸载荷,t、w和d分别为层合板的厚度、宽度和孔径.

图3 拉伸特征长度的定义
Kweon[3]指出,带孔层合板的拉伸特征长度不会随着拉伸载荷大小发生变化.
1.4 失效准则
本文采用以下6种失效准则[7-10]进行连接失效判断:

其中:σ1,σ2分别表示层合板各层纤维方向的正应力,τ12表示剪切应力,X、Y和S 分别代表纵向强度、横向强度和面内剪切强度.式(7)中的F 表示应力空间中的强度参数.
2 连接强度和失效分析
2.1 算例模型尺寸及参数
对文献[11-13]中的三种金属与复合材料单钉双剪试验件进行分析,试验件形式如图4所示,代号分别为AS,HP和DM,无紧固件预紧力.外侧金属板尺寸与中间复合材料层合板几何尺寸相同,见表1和图5.金属板和钉的材料均为钢,杨氏模量为210GPa,泊松比为0.31.复合材料板的材料性能见表2,AS 试件的铺层为[45/0/-45/0/90/0/45/0/-45/0]2s,HP和DM 铺层方式相同,均为[±453/90/ ±452/02]s,其中±45 表示纤维正交编织铺层,AS43501-6和USN125是单向层,HPW193和DMS2288 是编织铺层.

图4 单钉双剪试件模型

图5 试验件尺寸图示

表1 试验件尺寸(单位:mm)

表2 试验件复合材料性能
2.2 计算结果及分析
先将试件等效为含孔正交各向异性板.对板施加不同的纵向拉伸载荷(5、10、13 N),确定层合板的拉伸特征长度;再对钉施加不同的压缩载荷(3、6、8 N),通过钉与孔的接触挤压分析确定层合板的压缩特征长度.计算结果见表3.
从表3 可以看出,对同一试件施加不同的拉伸载荷,得到的拉伸特征长度Rt只存在微小的差异.从理论上讲,在线性条件下,拉伸特征长度与外载荷大小无关,同种试件的拉伸特征长度完全相同,表中的微小差异是属于有限元数值计算引起的误差.
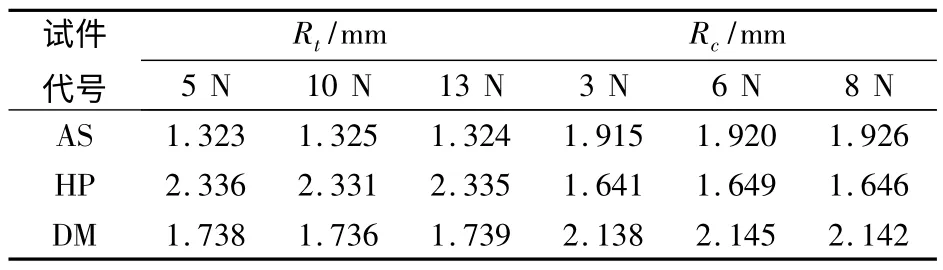
表3 拉伸和压缩特征长度
对同一试件施加不同的销钉挤压载荷,得到的压缩特征长度Rc之间的差异相比拉伸特征长度稍大,这是由于钉孔接触问题的非线性引起的,但是这种差异仍然小到可以忽略.
在确定特征长度Rc和Rt后,利用式(1)确定出带孔层合板的特征曲线.当特征曲线上的任意单元应力满足失效准则,则认为连接件失效,对应的外载荷就是连接件的失效强度.
本文采用Abaqus 有限元软件进行数值计算.选取特征曲线上的20个点,利用样条曲线插值逼近特征曲线,采用8 节点六面体线性减缩积分单元(C3D8R),接触面切向定义库伦摩擦,系数为0.1.接触法向定义为硬接触.网格划分如图6所示.

图6 模型网格
根据特征曲线上的应力,分别以上述6种失效准则作为失效判据来预测层合板机械连接的强度值,计算结果见表4,图7~9.

表4 不同失效准则下计算结果和精度

图7 不同准则下DM 的计算结果
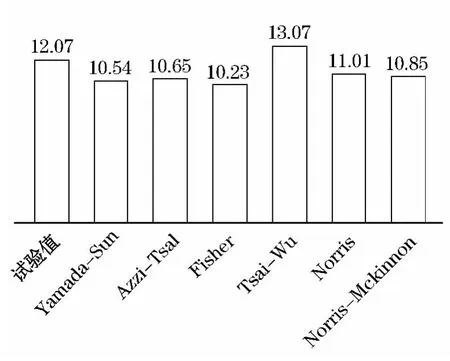
图8 不同准则下HP 的计算结果

图9 不同准则下AS 的计算结果
从计算结果上看,利用等效正交异性板计算拉伸和压缩特征长度,从而计算层合板的失效强度方法可行,计算结果在可接受范围内,推荐使用,从而简化计算过程,节省计算时间.对于本文三种试件AS,HP和DM,利用Tsai-Wu 准则计算误差是所有准则中最大的.虽然Tsai-Wu 准则考虑了拉压性能不同的复合材料,但是F12是估算值,对于不同性能的材料,F12的影响大小不一.Pipes和Cole[14]利用硼/环氧的各种偏轴试验测量了F12,指出偏轴拉伸时,F12有明显的变化,而对偏轴压缩则变化不大,所以,F12的不确定可能是引起误差的一个原因.此外,比较其他五种准则的计算结果,发现并没有任何一个失效准则可以完全适用于本文中的三种试件.以Fisher 准则为例,对于试件AS,Fisher 准则计算误差是所有准则中最小的,而对于试件DM,它的计算误差却达到-22.5%.而同种材料属性不同尺寸的层合板,利用不同失效准则,计算结果也完全不同,例如试件HP和DM,利用Azzi-Tsai 准则,DM 的计算误差仅为1.1%,而HP 的计算误差达到了-11.8%.因此,为了计算简便,推荐使用Yamada-Sun 准则.
3 结论
1)利用等效正交异性板,结合有限元分析,计算拉伸和压缩特征长度.再以计算的单层应力预测连接件的失效强度,可避免确定特征线的试验过程,降低试验成本,简化计算过程.
2)针对3个应用实例,考察不同的失效准则计算连接强度的效果.结果表明,6种失效准则中,Tsai-Wu 准则的误差最大,其他5种失效准则在对连接件失效强度估算中,计算误差相当,并没有任何一个特定的失效准则可以适用于所有试件的强度估算.因此,为了计算简单,推荐使用Yamada-Sun 失效准则.
[1]WHITNEY J M,NUISMER R.J.Stress fracture criteria for laminated composites containing stress Concentration[J].Journal of Composite Materials,1974,10:253–65.
[2]CHANG F K,SCOTT R A.Strength of mechanically fastened composite Joints[J].Journal of Composite Materials,1982(16):470.
[3]KWEON J H,AHN H S,CHOI J H.A new method to determine the characteristic lengths of composite joints without testing[J].Composite Structures,2004,66:305–315.
[4]CAMANHO P P,MATTHEWS F L.Stress analysis and strength prediction of mechanically fastened joints in FRP[J].Composites,1997,28A:529–547.
[5]陈鹏飞,赵美英.基于单层数值特征曲线法的复合材料接头强度方向[J].飞机设计,2008,4:41-45.
[6]ALUKO O,MAZUMDER Q.The Accuracy of Characteristic Length Method on Failure Load Prediction of Composite Pinned Joints[C]//Proceedings of the World Congress on Engineering,London,2010,II:1-6.
[7]HASHIN Z.Failure criteria for unidirectional fiber composite[J].Journal of Composite Material,1980,47:329–340.
[8]NAHAS M N.Survey of failure and post-failure theories of laminated fiber-reinforced composites[J].Journal of Composites Technology and Research,1986,8(4):138-153.
[9]TSAI S W,WU E M.A general theory of strength for anisotropic materials[J].Journal of Composite Materials,1971,5:58-80.
[10]HASHIN Z,ROTEM A.A fatigue failure criterion for fiber reinforced materials[J].Journal of Composite Materials,1973,7:448-464.
[11]BURK R C.Standard failure criteria needed for advanced composites[J].Astronautics and Aeronautics,1983(22):58-62.
[12]WHITWORTH H A,OTHIENO M,BARTON O.Failure analysis of composite pin loaded joints[J].Composite structures,2003,59:261-266.
[13]CHOI J,CHUN Y.Failure load prediction of mechanically fastened composite joints[J].Journal of composite materials,2003,37(24):163-2177.
[14]PIPES R B,COLE B W.On the off-axis strength test for anisotropic materials[J].Journal of Composite Materials,1973,7:246-256.
