双腔室空气弹簧的实验建模

武文山，周振华，金建新

(华中科技大学数字制造与技术国家重点实验室湖北武汉430074)

0 引言

随着超精密测量和制造技术的发展，由于精度的不断提高对环境振动的要求越来越严格［1］，隔振系统已经成为超精密测量和制造设备必要的一部分。对于隔振系统的低刚度、高衰减率的要求也越来越严格［2］。

超精密隔振系统的关键部分是空气弹簧，相比其它机械式和橡胶式的隔振器，空气弹簧的优点是利用空气的可压缩性实现以较小的刚度支撑起较大载荷。双腔室空气弹簧因为具有较低刚度和良好的阻尼特性的优点，而广泛应用在各种隔振系统中［3］。

图1所示为双腔室空气弹簧隔振器的原理图，其基本结构为通过一个节流孔连通上下两个腔室。空气弹簧的上方由一个刚性的活塞来支撑载荷(包括隔振平台和精密设备)，活塞和上腔室壁之间通过安装橡胶密封膜来防止空气泄漏。

图1 双腔室空气弹簧隔振器原理图

为了使空气弹簧隔振系统达到更优越的性能，结构参数优化和主动控制是两种有效的方法［4-6］，而这两种方法的应用都需要事先获得空气弹簧的精确数学模型。Shearer通过考虑腔室的热力学过程得到了空气弹簧的非线性模型［7］，Harris和Debra在活塞小位移运动的条件下推导出了线性模型［8，9］，但是其理论模型与实际测试数据之间存在较大差异。本文在实验的基础上分析差异存在的原因，将密封膜的影响考虑在模型内，并通过参数识别得到改进模型的传递函数。

1 空气弹簧的理论模型

要获得空气弹簧的理论模型，就是要建立输出量(活塞板的运动xp)对输入量(地面扰动xbase、干扰力Fd)的传递函数表达式。

双腔室空气弹簧在工作时，可认为活塞在其静态平衡位置附近作微幅运动。微幅运动过程中所产生的动态力引起上腔室中空气质量(mt)、压力(Pt)、体积(Vt)、温度(Tt)、节流孔中气流(mtb)，以及下腔室空气质量(mb)、压力(Pb)和温度(Tb)的变化，各变化量如图2所示。由于这一过程速度非常快，可近似视为绝热过程。根据能量交换可作出以下推导。

图2 变量示意图

1.1 腔室空气质量的变化

对于上腔室，使用开口系统的能量方程［10］：

其中，dQ为系统吸收(放出)的热量，对于绝热过程dQ=0;dW为系统所作的膨胀功，在小位移条件下有dW=P0dVt;dU为热力系自身能量的变化，其表达式如下：

dH在此处为空气流入节流孔引起上腔室焓的变化，因此有：dH=dmtCpTtI，其中TtI为节流孔在上腔室入口处的温度;e0和det分别代表初始内能和内能的变化量;Cp和Cv分别为等压比热容和等容比热容;将式(2)、式(3)及dW、dH的表达式代入式(1)中，得到：

根据shearer的理论，在小位移情况下，节流孔中的温度变化可以忽略不计，故有TtI=T0。将腔室中的气体假设为理想气体，因此有：

由式(5)和(6)，得到腔室中空气的质量、体积、压力和温度之间的变化关系式(7)，将式(7)代入式(6)中，得到式(8)。

其中，κ为比热比κ=Cp/Cv。对于下腔室，类似地有：

1.2 节流孔中的质量流速

对于节流孔，设经过气管进入到下腔室的流量为Qb，节流孔中的质量流速为，则有下述关系：

根据细长孔(l/d＞4)的压力流量特性：

q=pd4Δp/(128 ml)，得到：

其中，Cr为流量系数，Cr=pd4/(128 ml)，μ为空气粘度。

1.3 传递函数

对活塞，应用牛顿第二定律，得到：

其中，mp为活塞和载荷的质量;Fd为施加到活塞上的干扰力;Ap为活塞的有效面积;vp为活塞的运动速度;Patm为外界大气压;Vt为上腔室的体积，其表达式为：

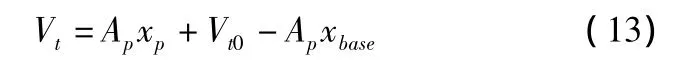
将式(11)代入式(10a)，再代入式(8)，并将式(13)代入式(8)得到：

由于活塞可视为在静态工作点附近做小幅运动，其振动幅值范围为0～20 μm，故可以将其线性化：

同理，将式(11)代入式(10b)，再代入式(9)，得到：

由式(12)可得：

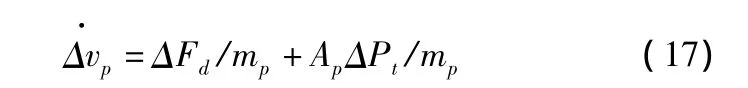
对方程式(15)、式(16)、式(17)进行拉普拉斯变换，可得：

联立式(18)、式(19)、式(20)三式，可得传递函数：

其中：

2 模型检测实验与分析

2.1 实验设计及结果

一个可使用的数学模型需要能够精确地预测系统的特性，为了检测空气弹簧理论模型的有效性，将理论传递函数与实测数据进行对比。

图3为实验装置简图，其包括空气弹簧、音圈电机、传感器、数据采集器及PC主机。使用NI测控系统控制音圈电机对空气弹簧的活塞板进行激励，由动态力传感器获得激振力信号，速度传感器获得空气弹簧的速度响应(速度传感器安装在活塞板上)，传感器采集到的信号经过调理后进入LMS数据采集系统，然后由软件进行频谱分析得到响应速度对激振力的实测传递函数。

图3 实验装置图

实验采集的输出量为活塞板的速度，其对激振力的理论传递函数可由式(21)经变换得到：

实验测得传递函数与理论传递函数的对比如图4所示。可以看到，共振峰出现的位置及峰值的大小均存在较大的偏差。理论传递函数中，系统的共振频率为1.76 Hz，而实测曲线表明共振频率为2.64 Hz。

图4 实测传递函数与理论模型对比

2.2 实验结果分析

理论传递函数和实测曲线之间共振频率和共振峰存在偏差，表明理论模型对系统实际刚度和阻尼的预测不准确。在理论模型中，系统的刚度主要由空气弹簧腔室的尺寸和载荷大小决定，阻尼主要由节流孔的尺寸决定。在图3所示的实验装置中，以上相关尺寸都是确定已知的。在建模过程中，唯一没有考虑的元件是橡胶密封膜，因此需要重新考虑其对系统刚度和阻尼的影响，进而对模型进行修正。

密封膜的材料为中间加入一层涤纶布的丁腈橡胶，由于橡胶结构件可能引入非线性影响，因此需要进一步探究密封膜对空气弹簧的影响是否与激振条件有关(激振的幅值、频率等)。文献［4］的研究表明节流孔具有非线性的特性，因此为了消除节流孔的影响，设计了图5所示的单腔室实验。图5(a)为空气弹簧的单腔室装置图(去掉节流孔，将上下腔室打通)，图5(b)为逐渐增加激振力的幅值大小(从0.02到0.14)测得的一系列传递函数。可以看到，在激振幅值变化时，传递函数曲线基本上是重合的。因此可以得出结论，在该实验条件下，密封膜的刚度和阻尼可视为常值。

图5 单腔室实验

3 空气弹簧的改进模型

3.1 改进模型的提出

根据第2节的实验结果及分析，将密封膜的模型简化为弹簧(Km)、粘性阻尼(Cm)与结构阻尼(Cd)的组合。对于结构阻尼，其应力－应变曲线为一个滞后回线。此回线所围的面积表示一个循环中单位体积的材料所消耗的能量，这部分能量以热能的形式耗散掉，从而对结构的振动产生阻尼。材料阻力在一个周期内所消耗的能量ΔEs与振幅的平方成正比，而在相当大的范围内与振动频率无关［11］，即有：

在小振幅的条件下(＜20 μm)，这部分的影响可以忽略不计，因此密封膜对模型的影响可以等效为弹簧(Km)加粘性阻尼(Cm)，如图6所示。

图6 考虑密封膜的模型

在考虑密封膜的影响后，活塞板的动力学方程为：

对上式进行拉普拉斯变换可得：

联立求解式(18)、式(19)、式(22)，可得修正后的传递函数为式(23)，其中Km，Cm为未知参数，可通过参数识别确定具体值。

其中：

3.2 参数拟合

由于理论模型中，节流孔的流量系数Cr为经验公式，因此在参数识别中，将Cr作为未知参数处理。

参数拟合采用麦夸特算法，即阻尼因子法，其基本思想是在高斯－牛顿算法中得到的矩阵A中加一项阻尼因子，其收敛性优于高斯－牛顿法，在计算初值较差的情况下仍较易收敛。使用1stOpt软件编制相应程序进行参数拟合，表1为软件运算收敛后各优化评价参数的值。

表1 参数优化结果

最终得出Km和Cm的最佳估算值为：

将最佳估算值代入到式(23)中得到改进模型的传递函数，将其与理论模型及实测曲线进行对比，如图7所示。可以发现，在考虑了密封膜结构的影响之后，与理论模型相比，改进模型更接近实测曲线。其中在共振峰附近改进模型与实测数据有较高的拟合度，而在较低频段及较高频段，改进模型仍不能较好地吻合实验数据。其中一个重要原因是节流孔的阻尼特性尚未有成熟的理论公式，文献［4］研究了节流孔的开口大小对阻尼的影响，而该实验结果也可作为进一步研究节流孔阻尼机制的参考。

图7 改进模型与理论模型对比

4 结论

双腔室空气弹簧理论模型与实测数据之间存在较大的差距，本文在实验数据的基础上分析了橡胶密封膜对空气弹簧模型的影响，通过对实验数据进行分析，将密封膜简化为一个弹簧和一个阻尼并联。将密封膜的刚度和阻尼作为未知参数建立新的模型，通过参数优化得到未知参数的值，改进模型与原有模型的对比表明了改进模型的有效性。由于节流孔的阻尼机制尚未清晰，因此本模型具有一定的局限性。

［1］C.G.Gordon，Generic criteria for vibration－sensitive equipment［C］//Proceedings of SPIE，San Jose，CA，1991.

［2］Eric H.Anderson，Bowie Houghton，ELITE－3 active vibration isolation workstation［J］.Smart Structures and Materials2001：Industrial and commercial applications of smart structures technologies，2001，pp.183 –196.

［3］Cyril M.Harris，Allan G.Piersol，Harris’Shock and Vibration Handbook，5th Edition［M］.McGraw － Hill，2001.

［4］Jeung－Hoon Lee，Kwang－Joon Kim，Modeling of nonlinear complex stiffness of dual－chamber pneumatic spring for precision vibration isolations［J］.Journal of Sound and Vibration301(2007)909–926.

［5］ Abu Hanieh.Active Isolation and Damping o f Vibrations via Stewart Platform［D］.Brussels：ULB Active Structures Laboratory，2003.

［6］Yoshioka H，Takahashi Y，Katayama K.An Active Microvibration I-solation System for Hi－ tech Manufacturing Facilities［J］.Journal of Vibration and Acoustics，2001，123：269 －275.

［7］J.L.Shearer，Study of pneumatic processes in continuous control of motion with compressed air［C］//Transactions of ASME78(1956)233－242.

［8］ C.M.Harris，C.E.Crede，Shock and VibrationHandbook［M］.McGraw －Hill，New York，1961.

［9］ D.B.Debra，Design of laminar flow restrictors for damping pneumatic vibration isolators，CIRP Annals33(1)(1984)351－356.

［10］黄晓明，刘志春，范爱武.工程热力学［M］.武汉：华中科技大学出版社，2011.

［11］师汉民.机械振动系统－分析·测试·建模·对策［M］.武汉：华中科技大学出版社，2004.