球杆系统的数字滤波与控制

傅彩芬， 房 方

(华北电力大学控制与计算机工程学院，北京 102206)

0 引言

在控制领域中，非线性不稳定系统的建模和控制器的设计有许多难点。而实际工业环境中各种非线性系统，由于绝大多数不稳定系统都具有危险性，研究起来有一定的困难，而球杆系统可以很好地解决这个问题。球杆系统是一个非线性不稳定系统，它简单、安全并且具备了非线性不稳定系统所具有的重要动态特性。因此作为控制理论研究中的一种比较理想的实验手段，球杆系统为自动控制理论的教学、实验和科研构建了一个良好的实验平台。

目前对球杆系统的研究通常是用来检验控制策略的效果，有基于经典控制理论的PID控制、根轨迹控制、基于频率响应的设计方法[1-2]，还有基于现代控制理论的最优控制[3-4]，鲁棒控制[5-6]，模糊控制[7-8]，以及自适应控制[9-10]和模糊PID控制[11-12]等方法。但是对于球杆系统工作过程中存在外界噪声干扰的分析较少。而实际系统运行过程中总会存在一定的电气干扰和其它因素，使得采集到的信号存在高频杂波信号，对于控制系统的稳定性和控制精度都会产生影响。特别是对于微分控制的控制系统，由这些杂波信号产生控制量往往比实际控制量还要大很多，系统变得不可控制。因此我们在采集到小球位置信号后需要进行滤波。对于此问题[1]设计了一个低通滤波器用于减少噪声和干扰，文献[13]采用卡尔曼滤波的方法对于系统的控制噪声和测量噪声进行了探讨。本文将采用线性和非线性两种滤波方式对球杆系统进行滤波分析，具体采用均值滤波，低通滤波，中值滤波三种数字滤波方法进行讨论，设计了相应的滤波器，并通过对球杆系统的闭环控制实验测试验证了三种滤波方法能有效地提高小球位置测量信号的准确性，从而提高了闭环系统的控制性能，为球杆系统的进一步控制优化研究提供参考。

1 球杆系统

球杆系统是一种在国内外自动控制领域广泛使用的实验系统，有多种结构形式，但其基本原理相同，主要应用于科学研究。在传统球杆系统的基础上，深圳固高科技公司研发了新一代球杆实验系统[1]，其组成结构如图1所示。

图1 球杆实验系统组成结构图

该系统的控制目标是在最短的时间内将小球准确移动到横梁的指定位置上。实现该目标的手段是通过改变伺服电机的转角，驱动传动轮和杠杆臂，进而改变横梁的倾斜角以调整小球在横梁上的位置。由于采用了先进的嵌入式数字控制器，实验过程的各状态数据及控制信号能够在计算机上显示并方便地进行存储和管理。该系统可以支持直线位移/角位移测量实验、直流伺服电机控制实验、电机调速实验、系统建模实验及各种控制算法的设计与实现等。

尽管有诸多优点，球杆实验系统在实验教学中还是存在不足，其中最突出的是由于小球位置传感器在设计和选型上的缺陷引起的位置信号干扰大、准确性差的问题。

2 小球位置信号的数字滤波

球杆系统中小球位置检测装置的结构如图2所示。

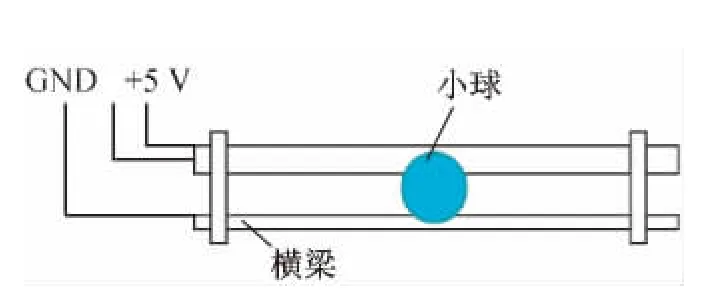
图2 小球与横梁共同构成的位置检测装置原理图

金属小球与横梁共同构成一个滑动变阻器，随着小球在横梁上位置的改变，其导通电阻的阻值会相应发生变化，送入AD转换器的电流信号也会随之变化。

由于金属小球只是简单地放置在横梁上，在快速滚动时由于微小震动会使小球短暂跳离横梁，引起位置测量信号出现不规则、大幅度、脉冲型的跃变;另外，若小球表面附着灰尘，也会影响导电效果，进而导致位置信号的变化。

为了消除附加在位置测量信号中的噪声，使采集到的数据能够真实反映小球的实际位置，加入数字滤波处理。分别采用线性和非线性两种滤波方式对球杆系统进行数字滤波分析，采用的方法分别为均值滤波、窗函数法低通滤波和中值滤波。这几种方法是可以用于工控软件中的一般的数字滤波技术，能够满足一般的数据处理需要。

2.1 均值滤波法

领域平均法是最常用的一种均值滤波方法，即:在一个周期内的不同时间点取样，然后求其平均值。该方法可以有效地消除周期性干扰。同样，这种方法还可以推广成为连续几个周期进行平均，计算公式为:

式中:Xn为实际采样值;Yk为滤波后结果;n为采样数;N为滤波窗口内的像素数目。均值滤波相当于低通滤波器[14]，在平滑噪声的同时，会模糊信号的细节和边缘。

2.2 低通滤波法

来自现场的信号的变化一般比较缓慢，而干扰一般带有突发性的特点，变化频率较高，而低通滤波器就可以滤除这种干扰。低通滤波器在信号处理中的作用等同于其它领域如金融领域中移动平均数所起的作用，简单理解就是抑制高频信号，通过低频信号。数字低通滤波器可采用无限长冲激响应(IIR)滤波器和有限长冲激响应(FIR)滤波器两类不同设计方法来实现。IIR数字滤波器是一类间接设计方法，其特征是:具有无限持续时间冲激响应。这种滤波器一般需要用递归模型来实现，因而有时也称之为递归滤波器。FIR数字滤波器是一类直接设计方法，其特征是:冲激响应只能延续一定时间，主要采用非递归结构，无反馈，但在频率采样结构等某些结构中也包含有反馈的递归部分。FIR数字滤波器的优点[15]是很容易获得线性相位，另外，FIR数字滤波器的单位脉冲响应是有限长，极点都位于原点，一定是稳定的。FIR数字滤波器还可以用FFT实现，从而大大提高运算效率。本文即采用FIR数字滤波器的窗函数法设计低通滤波器。窗函数可采用不同的形式，如:Bartlett，Blackman，Hammig，Hanning，Boxcar等。

2.3 中值滤波法

中值滤波[16]是基于排序统计理论的一种非线性信号处理技术，具有良好的边缘保持特性和抑制脉冲噪声的能力。对于窗口长度n=2k+1(k为正整数)的中值滤波器，设第i时刻输入信号序列在窗口内的样本为(xi－k，…，xi，…，xi+k)，则此时中值滤波器的输出为:

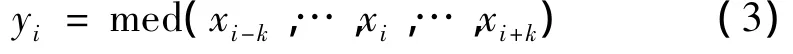
式中:med()表示取窗口内所有数的中位数。信号序列中脉冲宽度小于或等于k的脉冲信号，经过中值滤波后将被去除;当脉冲宽度大于或等于k+1时，经过中值滤波后脉冲则被保留[17]。

3 球杆系统数字滤波与控制

采用以上三种滤波方法对球杆系统采集到的小球位置信号进行滤波处理，结果如图3～5所示。其中均值滤波法采用的采样数为5;低通滤波器为5阶，采用的是Barlett窗;中值滤波法采用的周期数量为5。三种方法在测试中都起到了良好的滤波作用。

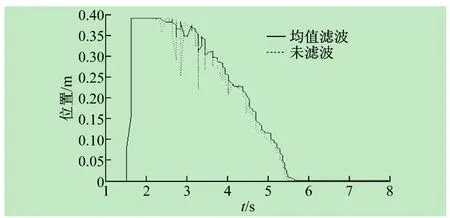
图3 均值滤波图

图4 低通滤波图

为了进一步验证加入数字滤波处理后球杆实验系统的运行效果，我们对其进行了闭环控制实验。控制器基于根轨迹法设计，在Matlab/Simulink环境下与实验系统进行实时通信连接。控制目标是使小球从任何初始位置出发，在最短时间内准确达到并停留参考目标位置。

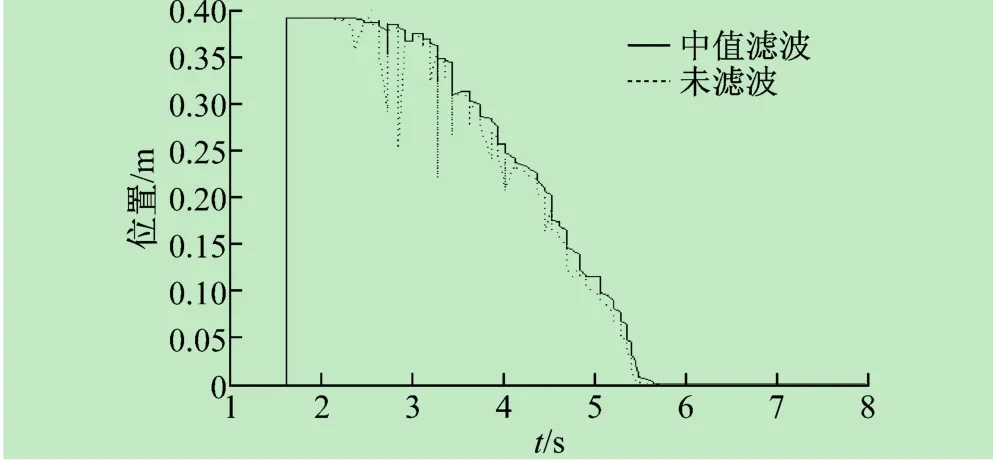
图5 中值滤波图

图6～8分别为采用均值滤波，低通滤波，中值滤波三种不同滤波器下的球杆实验系统的控制效果与未使用滤波器时的控制效果的比较。显然，经过滤波处理后，系统动态过渡过程更为平滑，既提高了系统运行的稳定性，也减少了执行机构的频繁动作。

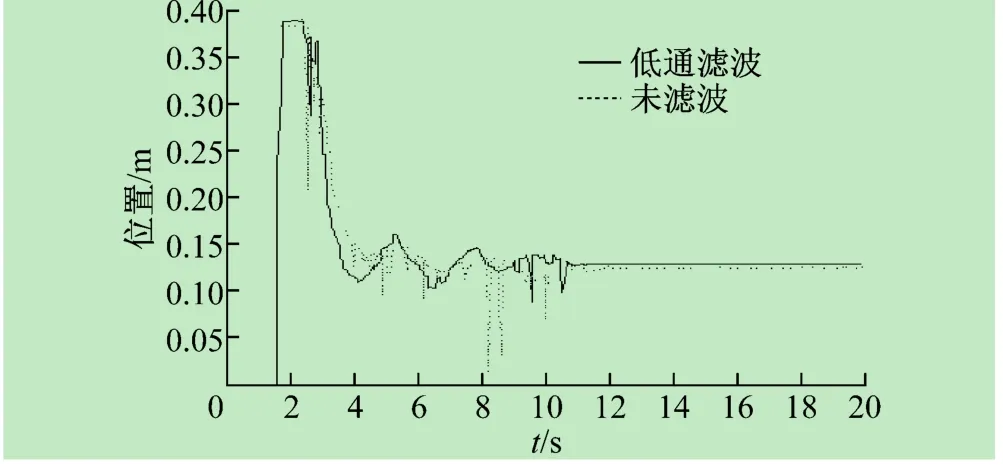
图6 均值滤波控制图

图7 低通滤波控制图

图8 中值滤波控制图

4 结语

本文针对球杆实验系统中小球位置测量信号干扰大、准确性差的问题，利用均值滤波，中值滤波，低通滤波等三种数字滤波方法对其进行改进，并通过实验验证了所采用滤波方法的有效性。

本文的研究表明，在融合了机械、电子、信息系统的先进实验装置中，对信号实施数字滤波的实现过程简单、成本低廉，是提高实验系统性能的有效手段。

[1] 固高科技(深圳)有限公司.球杆系统GBB1004用户手册与实验指导书[Z].固高科技有限公司，2006.

[2] 张志勇，何东健，张建锋，等.基于MATLAB环境下球杆系统PID控制器设计[J].农机化研究，2006(5):103-105.

[3] 王 青，崔海华.基于遗传算法的球杆系统最优控制器的设计[J].实验技术与管理，2009，26(4):42-46.

[4] 徐琼琼.基于LQR的球杆系统最优控制器设计[J].景德镇高专学报，2007，22(4):5-6.

[5] 胖永新.鲁棒控制理论在球杆系统中的应用[D].武汉:武汉大学，2005.

[6] 闫 鹏.基于RTW球杆系统H_∞控制设计[D].哈尔滨:哈尔滨工业大学，2007.

[7] 李保林，袁 浩，陈嘉贤.模糊控制方法在球杆系统中的应用[J].实验技术与管理，2008，25(1):87-90.

[8] 彭建刚.球杆系统的模糊控制仿真研究[D].哈尔滨:哈尔滨理工大学，2008.

[9] 刘克平，史鹏飞.球杆系统自适应遗传PID控制[J].科技通报，2009，16(2):173-175.

[10] 乔廷婷，卢秀和，刘晓庆.自适应神经网络控制器在球杆控制系统中的应用[J].微电机，2009，42(3):79-81，96.

[11] 宫 彬，球杆系统的模糊PID控制研究[D].哈尔滨:哈尔滨工程大学，2009.

[12] 彭秀艳，宫 彬.球杆系统的控制方法研究[J].应用科学，2009，36(12):37-40.

[13] 卢秀和，魏 坤，谢新月.卡尔曼滤波器在球杆系统噪声抑制中的应用[J].南京信息工程大学学报:自然科学版，2009(1):93-96.

[14] Oppenheim A V，Schafer R W.Digital signal processing[M].New York:Prentice-Hall Inc，1975.

[15] 杨玉霞，许 珉，廖晓辉，等。信号分析与处理[M].北京:中国电力出版社，2012.

[16] Gallagher N C，Wise G L.A theoretical analysis of the properties of median filters[J].IEEE Trans on Acoust，Speech and Signal Processing，1981，ASSP-29(6):1136-1141.

[17] Flandrin P，Rilling G，Goncalves P.Empirical mode decomposition as a filter bank[J].IEEE Signal Processing Letters，2004，11(2):112-114.