层片轮廓边界离散的双圆弧局部逼近算法

张 燎

ZHANG Liao

（甘肃工业职业技术学院，天水 741025）

0 引言

在RP制造技术中，三维 CAD 模型分层所得到的截面轮廓是由直线段、圆弧、椭圆弧及非均匀有理B样条曲线段等基本图形组成的折线多边形理论轮廓，在离散提取截面轮廓边界数据时，现在的RP成型设备常用直线插补的方式进行轮廓扫描，即按照一定规则将离散点直接选定在边界曲线段上，取出一系列离散点，然后将各离散点用直线段连接起来，形成物理层片加工的实际折线扫描路径，这样处理的结果会导致实际扫描轮廓和理论扫描轮廓之间存在较大的形状和尺寸偏差，而且会丢失轮廓的一些细节信息（如图1所示），特别在离散曲率较大的截面理论轮廓时，丢失的信息会更多，产生的偏差更大，使打印出的三维实体“失真”。

图1 直线插补离散形成的实际扫描轮廓

为解决直线插补离散产生的形状和尺寸偏差问题，可用双圆弧和直线插补混合的方法离散理论扫描轮廓。当轮廓曲率大于预定值时，用双圆弧逼近法局部离散扫描轮廓，反之，则用直线插补法离散，以提高离散速度。

1 双圆弧逼近算法的构建

双圆弧成立必须具备6个条件，其定义见文献[1,2]；双圆弧是根据双圆弧圆心角的符号来划分类型的：若两弧度角符号相同，即同为正或负则此双圆弧为C型，如图2(a)所示；若两弧度角符号不同，即一个为正一个为负，则此双圆弧为S型，如图2(b)所示。

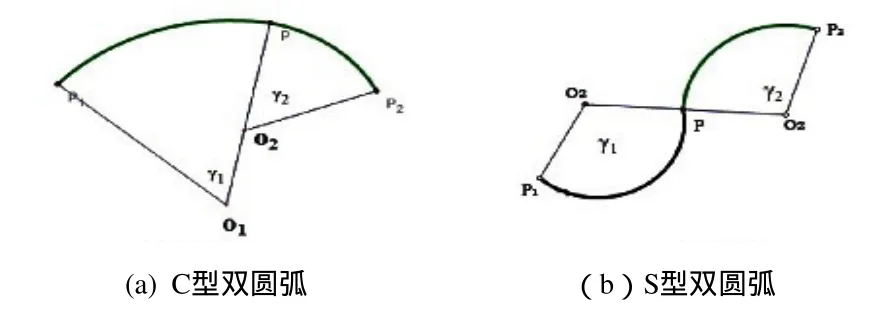
图2 双圆弧的基本分类

1.1 坐标系

为了建立双圆弧逼近算法模型，在图3中建立以P1点为原点、矢量为X轴和垂直于x轴的一矢量构成y轴的直角坐标系，规定各角度逆时针为正，顺时针为负，这样α1和β1为正，而α2和β2为负，其中α1和α2分别为P1点和P2的切线角，P点将圆弧P1P2（局部轮廓）分割为两段简单圆弧P1P和P2，P点被称为两段圆弧的连接点。

1.2 双圆弧连接点确定的原则

双圆弧逼近就是不断寻找两段弧的连接点 Pi，并将它取出，这是双圆弧逼近算法实现的一个关键问题。为使两个圆弧连接尽可能的光顺[2]，采用“使两段圆弧曲率之差最小”的原则来确定点P的位置[3]。

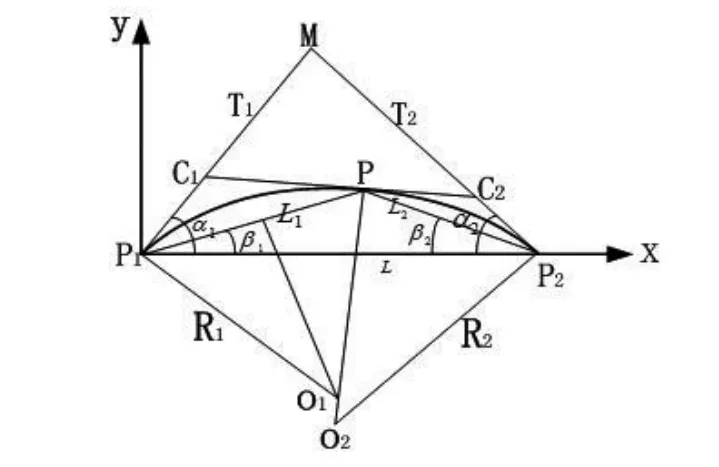
图3 两节点P1和P2之间的双圆弧

1.3 双圆弧逼近算法的构建

1）双圆弧的相对曲率半径

利用图3中的的几何关系和正弦定理，可导出双圆弧相对曲率半径R1、R2的计算公式。

曲率之差绝对值的最小值为:

通过求解(4)式的极小值，可求得使双圆弧局部光滑的1β和2β：

将式（5）带入式（1）和式（2）可得：

由图3可看出，双圆弧的半径已求得，只要求得两段圆弧的圆心O1和O2的坐标和连接点P的坐标，就能确定任意两个离散点之间的双圆弧。

2）双圆弧的圆心坐标

圆弧O1的坐标为：

圆弧O2的坐标为：

3）连接点P的坐标

4）求出各点的切矢

由式（6）～式（9）可看出，圆心、连接点和圆弧的半径的确定是以层片理论轮廓起始的两个点推导出来的，对于后续拟合的点同样适用。要确定相对曲率半径、双圆弧的圆心坐标和连接点的坐标(需要确定α1和α2)，还要确定各点的切矢。

由双圆弧的定义可知，每条双圆弧必须要有4个已知条件及一个判据才能确定[2]，而判据和两端点坐标、各离散点的坐标都已知，这样连接点处的切线矢量从层片数据中插补获得。已知三个连续的边界点Pi−1、 Pi和Pi+1，如图4所示，则 Pi点处的切线矢量为：

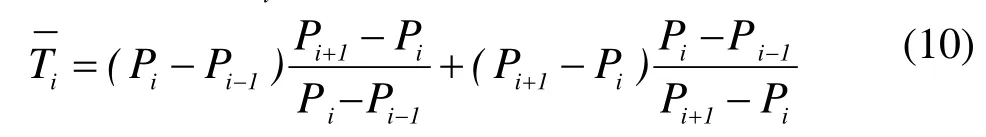
图4 层片数据的切矢

求得各点的切矢后，就可以求出αi了，由矢量的运算可得其公式为：

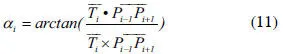
其符号由以下行列式判断：

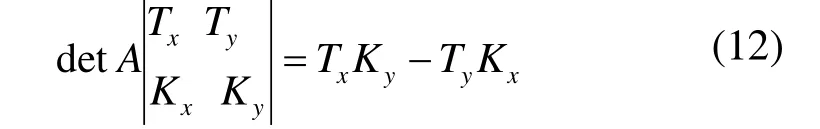
式中，Tx,Ty分别为矢量的x，y分量，Kx,Ky分别为矢量的x，y的分量。在图3建立的坐标系中，若该行列式值大于0，则矢量元在X轴的上方，αi＞0；相反，则αi＜0。

1.4 双圆弧逼近的误差

通过每段圆弧圆心到连接点Pi的距离减去该段的半径来计算逼近的误差。

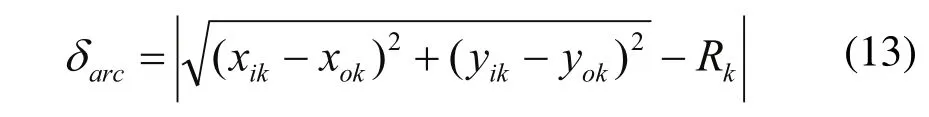
其中i代表 P1和Pn之间的等分点Pi的下标，k代表连接点Pik(xik,yik)对应的第一段圆弧还是第二段圆弧的下标。P(xok,yok)和Rk分别对应圆弧的圆心、半径，(xik,yik)为连接点 Pi的坐标。

1.5 坐标转换

圆心坐标、连接点坐标都是在局部坐标系（oxy）中求得的，还要转换到整体坐标(oμv)中，其转换关系为：

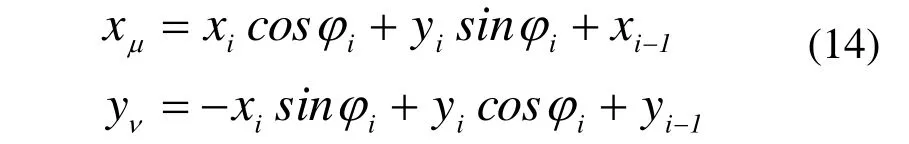
其中(xi−1，yi−1)为起始点坐标，φi为双圆弧的两端点连线 Pi−1Pi+1与总体坐标系μ轴正向的夹角。（xi，yi）为局部坐标系中的任意一点坐标。

2 算法实施的步骤

Step1：将层片的扫描轮廓边界分解为基本图形元素组成的曲线组，结果存放在一动态曲线段数组中。按曲线段成员首尾相接的拓扑关系，将其在数组中的存放次序重新排列。

Step2：定义一点对象动态数组存放扫描轮廓曲线离散结果。首先取曲线段数组中第一个成员作为当前处理对象。

Step3：按照等步长对理论轮廓数分割，找出极值点和奇点。

Step4：计算两端点的曲率，如果大于零则调用双圆弧逼近处理程序，转入Step5，如果曲率接近于零，用直线插补法离散，转入Step8。

Step5：求出相邻两个节点处的切矢，这样每2个节点间可以用前述的双圆弧方法逼近。

Step6：计算出两个圆弧的相对曲率半径和圆心坐标后，可求得两圆弧连接点的坐标，这样就构造出逼近层片理论局部轮廓的双圆弧。

Step7：进行误差检验。如果逼近误差小于给定误差限δ，逼近就结束，可进入下一轮相邻边界点的双圆弧逼近，转入Step4，如果大于给定误差，则将两个理论轮廓的端点再等分（实际上是变步长），转入Step4过程，直到精度满足为止。

Step8：将离散的节点数据存入数组。

3 算法验证

理论扫描路径如图5中细实线部分，它由三条直线段和一条NURBS曲线段组成，轮廓边界框大小为 203.756×129.869，为了清楚地看出直线插补和双圆弧局部逼近两种算法离散曲率较大轮廓产生的效果，将离散的步长取大一些，取d=10、15、20三个步长，分别计算三组数据。在采用C#编程实现[4]算法时，直线插补离散差生的误差，用两段圆弧连接点 Pi到被双圆弧分割的局部轮廓两端点连线之间的距离δline表示，双圆弧离散产生的误差用文章提出的双圆弧局部逼近算法中的误差δarc表示，两种轮廓离散方法的效果对比列于表1中。

由表1看出，随着步长的增大，两种算法的误差也随之增大。在同一步长下，双圆弧算法产生的误差要比直线插补算法产生的误差要小一半，说明双圆弧离散曲率较大的轮廓时，逼近程度要高，效果明显（见图5中1和2放大部分）。但对于曲率较小的轮廓，双圆弧的效果不是明显。

表1 直线插补和双圆弧局部逼近算法所差生的误差比较

直线插补和双圆弧局部逼近离散的实际扫描轮廓对比见图5粗实线部分。

图5 直线插补离散和双圆弧局部逼近离散对比(d=20)

文章还将双圆弧局部离散算法的离散效果与中国矿业大学王卫辰关于“面向快速成形的三维CAD模型直接分层方法研究”[5]论文研究成果也进行了对比。王卫辰等人对曲率较大的轮廓离散时，采用的是变步长离散方法，即小步长离散。对于同样的轮廓，双圆弧局部离散效果要比变步长离散逼近效果要好。

4 结束语

经过验证，双圆弧局部逼近离散算法是可行的，能明显减小现有成型设备采用直线插补法离散曲率较大的理论扫描轮廓产生的偏差，与直线插补离散法相比，双圆弧离散误差减小了约50%。在算法实施的过程中，使用了双圆弧局部逼近和直线插补混合算法，曲率比较大的轮廓用双圆弧逼近，曲率接近于零的轮廓用直线插补法离散，既提高了精度，也避免了单纯采用双圆弧逼近算法导致的运算速度下降问题，具有较好的工程使用价值。

[1] 苏步青,刘鼎元.计算几何[M].上海:上海科技出版社,1982 .

[2] 施雯.代数曲线的双圆弧逼近与等距线构造[D].杭州:浙江工业大学,2012:7-25.

[3] 上官建林.快速原型制造中反求工程关键技术的研究[D].郑州:郑州大学,2007:33-40.

[4] 王小科.C#开发实战宝典[M].北京:清华大学出版社,2010.

[5] 王卫辰.面向快速成形的三维CAD模型直接分层方法研究[D].徐州:中国矿业大学,2010,3: 90-93.