低温下理想气体的热容

2013-10-16马紫东宋友林

河南教育学院学报（自然科学版） 2013年2期

马紫东，王飞，张起，宋友林，贾瑜

(1.郑州大学物理工程学院，河南郑州 450001;2.河南教育学院物理系河南郑州 450046)

0 引言

统计力学通常以理想气体为例，通过对能均分定理的证明以及经典统计力学相关公式的应用得到在常温条件下理想气体的定容热容，其包含平动热容、转动热容Nk和振动热容个部分，而振动热容在常温范围内一般不予考虑［1］208.但是，若是按照上面的公式，定容热容在低温下应该仍然为常数，这一点显然与热力学第三定律的一个重要推论相矛盾，即在温度T趋近于零的时候物质系统的热容量应该趋于零.所以上面所提到的理想气体的定容热容只是限于常温下才能近似成立.本文通过运用量子统计力学的方法，利用波尔兹曼分布的配分函数并借助于计算机数值求解的方法来验证理想气体的平动、转动以及振动热容在温度趋于绝对零度时也是趋于零的.

1 模型与理论计算

本文以符合波尔兹曼统计的理想气体为模型来研究定容热容，为此先给出非简并理想气体的成立条件［2］，即，气体是理想的且是非简并的.当上述条件不成立时，应用量子力学理论讨论整个系统，因为此时的气体是简并的，波尔兹曼统计则需要根据所研究对象的不同分别被玻色－爱因斯坦统计或者费米－狄拉克统计所代替.所以基于上面两个条件的限定，就可以将确定整个气体能级的量子力学问题归结为确定单个分子能级的问题.

有鉴于此，首先依次给出系统的平动、转动以及振动的配分函数，然后根据统计力学的已知公式来计算相应的热容，以能清楚地看出热容在低温的条件下的确是趋于零的.

1.1 平动的热容

对于在三维空间中运动的粒子，因为其x、y、z 3个方向的运动互不影响，所以可将在三维空间中运动的自由粒子看做是3个在一维空间中运动的粒子.那么对于在一维空间中运动的自由粒子，其能量［1］171就应该是±2，…，因此对于符合波尔兹曼统计的粒子，其配分函数应该是

此处有两点需要注意:(1)对于平动的粒子，认为L2的数量级约为10－16［3］;(2)简并度ωl应取为1［4］164－165.

图1就是将平动的配分函数带入热容的公式中后所画出来的在低温下的近似图像.由图像可以看出:在趋近于绝对零度时，平动的定容热容会逐渐趋近于零;而后随着温度的上升，热容也逐渐上升，并最终趋近于常数，且这个常数也与经典统计中对热容的近似计算结果相近.至于图像中热容在随温度的上升过程中存在一个极大值的原因，则会在下面关于转动的讨论中一并说明(因为转动热容的图像同样存在这样的一个峰值，而原因则与平动的相同).

1.2 转动的热容

对于双原子分子转动的讨论需要分成异核双原子分子与同核双原子分子两种不同的情况.出于简化问题处理的目的，本文在此只考虑异核的双原子分子.而对于同核的双原子分子，因为其核是全同粒子，在量子场合下确定转动的配分函数还必须考虑同核的对称性或全同性原理以及同核的两个原子的自旋状态对分子转动波函数的影响(事实上，量子场合考虑的通常只有氢的两种同位素:H2和D2)［5］.由于其过于繁杂，本文在此将不作赘述.对于异核双原子分子而言，其转动能级为…，其中l为转动量子数，能级的简并度是分子的转动惯量(是两个原子的折合质量，ru是两个原子核之间距离的平衡值).所以转动配分函数就是，引入特征温度，则会有

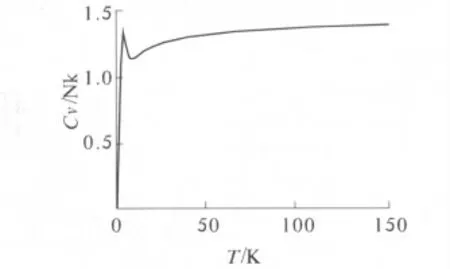
图1 低温下的平动热容Fig.1 The transitional heat capacity in low tem perature

而后借助于计算机求出异核双原子分子的转动热容随温度T的变化.

图2即CO分子(转动特征温度θr=2.77 K)的转动热容随T的变化.由图像可以很清楚地看出转动部分的热容同样是在达到一定的温度之后便几乎不再随温度的升高而有明显的变化.并且，其最终趋于稳定时的热容也与经典统计所求出的结果基本上保持一致，均为Nk.而达到稳定时所需要的温度同平动相似，都是远小于常温.除此之外，转动与平动的热容还有一个相似点就是随着温度的降低，热容在某一温度下趋于最终稳定时所需要取的配分函数中的项数逐渐减少.所以，此处不妨做一个近似的计算来研究转动热容图像上出现极大值的原因.在低温时一般只需要保留配分函数的前两项就足够了，因此有

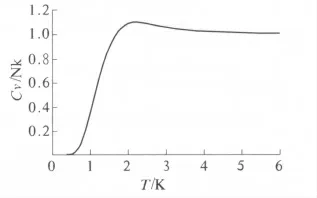
图2 转动热容Fig.2 The rotational heat capacity

1.3 振动的热容

由于气体热力学量的振动部分在高温时才开始占主要地位，所以在低温范围内通常可以认为振动能级基本上都没有被激发.这时振动是微小的(也是简谐的)，因而其能级可由量子力学中的线性谐振子来表示［4］178.对于双原子分子而言，其对应的热容［1］207

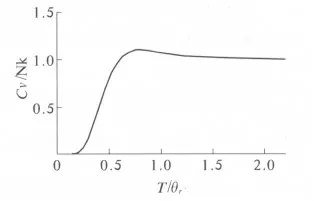
图3 转动热容随T/θr的变化Fig.3 The rotational heat capacity as a function of T/θr

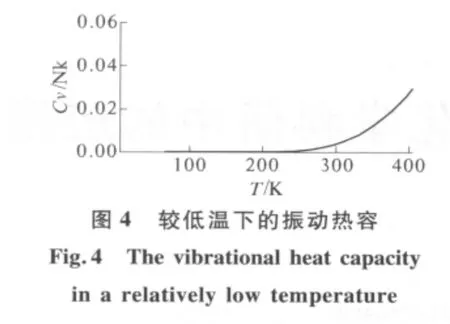
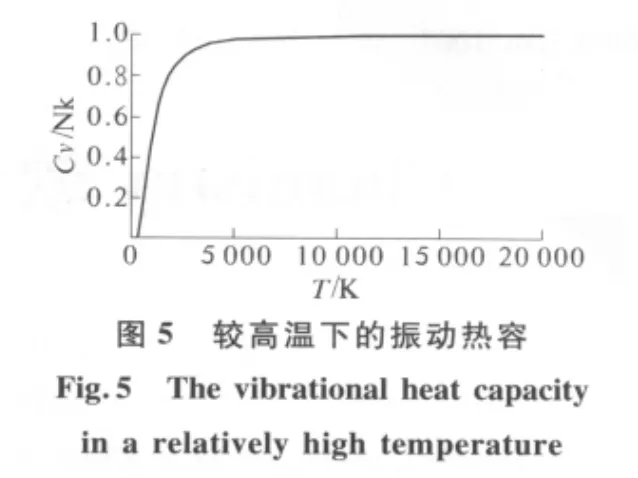
图4和图5是CO分子(振动特征温度θv=3.07×103K)的热容分别在低温和高温下随温度的变化图像.

由图4和图5可以看出，在低温区间振动所贡献的热容几乎为零.之后，随着温度的逐步上升，振动的热容才开始逐渐增大，并在温度达到104K这个数量级的时候才逐渐平稳，并最终趋于Nk.这也就是为什么通常在常温下不考虑振动热容的原因.

2 讨论

本文所提到的对于理想气体的近似模型实际上并不是完全正确的，因为在低温下，分子间距会变得非常小以至于无法忽略分子间的相互作用，而且这时所有的实际气体在足够低的温度下早已凝聚到一起了，此时理想气体模型的条件不再成立.实际上，热力学第三定律是要求在一定的体积取值下，物体的熵在T=0时应该变为零.但是在T→0时所有物质的饱和蒸汽压变得如此之小，以至于一定有限数量的物质在一定的有限体积下就不可能在T→0时还保持气态了.而若考虑一种永远不会凝聚的气体模型，则该模型在足够低的温度下波尔兹曼统计也无论如何不再正确［4］167.因为在此时(给定气体的密度并且温度足够低)，该统计中的粒子在各量子态的平均占据数不能假定为很小，所以实际上在极低温时，波尔兹曼统计应根据所讨论气体种类的不同分别过渡到玻色－爱因斯坦分布或者费米－狄拉克分布才行.但是因为本文主要是为了验证热力学第三定律的推论，以及给出一些热力学与统计物理的书上所没有明确提出的在低温下的热容具体是什么形式，所以采取了这种近似的理想化模型来简化计算过程，从而明确地看出热容在低温下的变化.