桥梁高墩计算长度的分析

2013-10-16董成

黑龙江交通科技 2013年8期

董成

(沈阳市市政工程设计研究院)

1 前言

某桥所处地形起伏较大，跨越深谷，两岸山坡陡峭。桥梁上部结构为15跨30 m桥面连续T梁桥，三跨一联，下部结构为三桩柱式墩，一柱对一桩，桥墩高度为18～34 m。双向四车道，桥面全宽20 m，设计荷载为城-A，基本风速按31.6 m/s，地震基本烈度为Ⅵ度。

对于具有较高高度的柔性桥墩，在竖向力和水平力的共同作用下，墩顶可能产生较大的水平位移，从而产生不可忽略的几何非线性效应，也称为P-Δ效应。桥墩是典型的压弯构件，对于本桥的高墩，墩柱长细比较大，在集中轴压力(上部结构支反力)、分布轴压力(墩柱自重)和水平力的作用下，这种P-Δ效应值得重视。

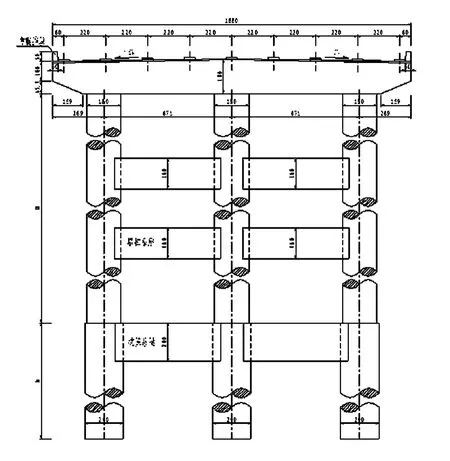
图1 桥墩一般构造图

2 理论分析

规范中将压弯构件的纵向力对截面重心轴的偏心距e0乘以偏心距增大系数η来考虑构件的P-Δ效应，η由下式计算:

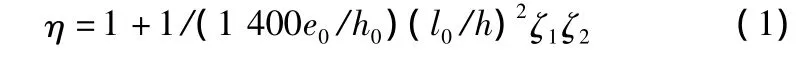
式中:l0为构件的计算长度;e0为轴向力对截面重心轴的偏心距;h0为截面有效高度;h为截面高度;ζ1为荷载偏心率对截面曲率的影响系数，ζ1=0.2+2.7 e0/h0≤1.0;ζ2为构件长细比对截面曲率的影响系数，ζ2=1.15-0.01l0/h≤1.0。

从公式(1)可知，确定η需先确定构件的计算长度l0。

在墩柱顶设有板式橡胶支座，而橡胶支座通过上部结构与其他墩及其橡胶支座相连，这样，在桥墩墩顶就形成一个弹性约束。

把桥墩作为悬臂竖梁，墩顶在产生水平向位移时，上部结构通过橡胶支座对墩顶施加水平约束，此时带有弹性约束的偏心受压墩的计算长度为:

α可通过下面的超越方程求得，即:

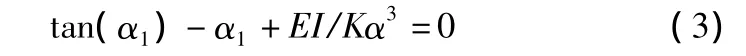
式中:l为桥墩自墩顶至假想固结点高度;EI为桥墩截面换算抗弯刚度;K为墩顶的水平约束刚度。

墩顶的水平约束刚度K值的计算模型如图2，求法为:将所求墩左右两侧的联合抗推刚度、并联，然后再将橡胶支座的抗推刚度并联，两者各自并联后再串联，从而得墩顶约束刚度，即K=(+)×(Ki1+Ki2)/［(+)+(Ki1+Ki2)］。

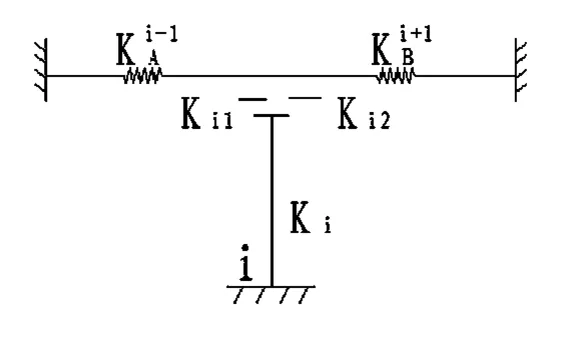
图2 墩顶约束刚度计算模型

求解计算K值过程中，涉及的主要参数为桥墩抗推刚度和支座抗推刚度，两者计算如下

(1)桥墩抗推刚度 Kd=3nEIh/(H3+δHH+δHHH+δHMH+δMHH+ δMMH2)，EIh为桥墩墩柱抗弯刚度，δHH、δHM、δMH、δMM为用“m”法计算桩基时有关参数，H为墩高，n为桥墩墩柱数。

(2)支座抗推刚度Ki1/2=nAG/t，n为一排支座的个数，A为一个支座的平面面积，G为橡胶支座剪切弹性模量，t为支座橡胶层厚度。

3 桥墩计算

由于桥墩墩高变化较大，墩身刚度直接影响相邻桥墩墩顶弹性约束，由公式(3)可知，因墩顶的水平约束刚度K不同，将影响桥墩的计算长度l0、偏心距增大系数η的值。因此，计算取各联中不同墩高组合分别计算，各墩高组合计算参数如表1。

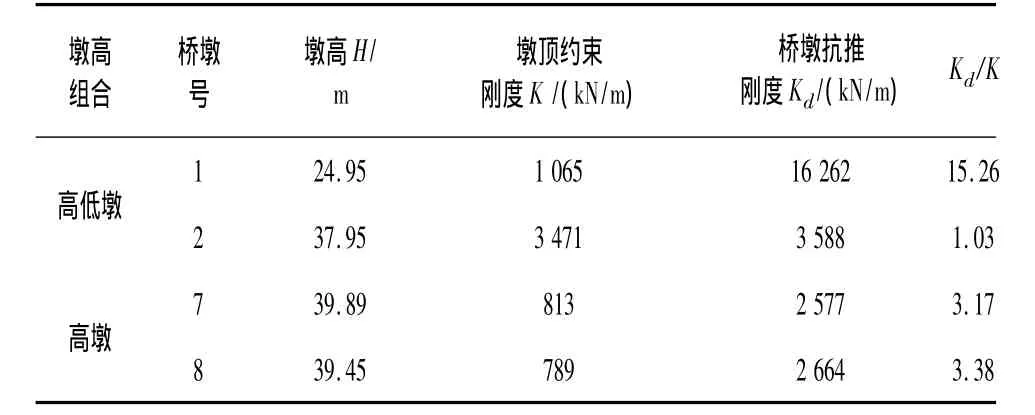
表1 桥墩计算参数

其中墩高考虑谷底冲刷深度、桩基固结深度。

墩顶计算荷载考虑恒载、汽车荷载、人群荷载、升温、降温、收缩、徐变、制动力、风荷载，取不利荷载组合。

当构件两端约束条件为一端固定一端为不移动的铰时，计算长度系数为0.7;当一端固定一端自由时，计算长度系数为2;而一端固定一端为弹性约束时，计算长度系数应视约束刚度的大小在0.7～2之间。

根据公式(1)～(3)可得桥墩计算结果如表2。

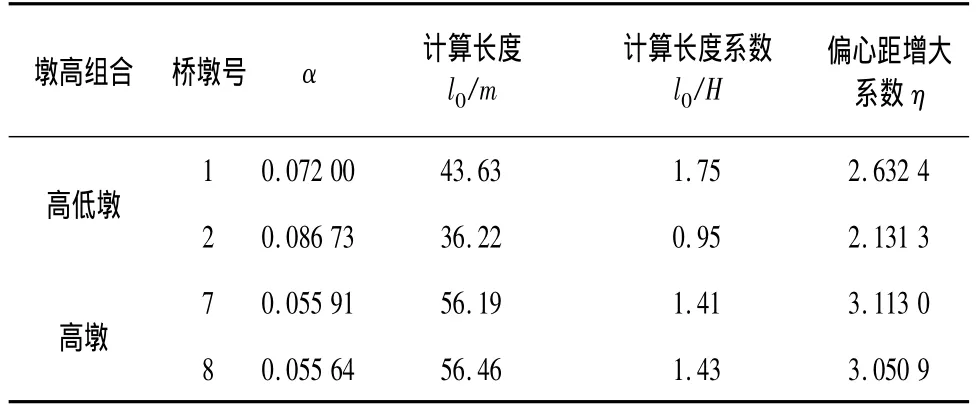
表2 桥墩计算结果

由表2中计算结果可知:

(1)根据桥墩抗推刚度和墩顶约束刚度的比值Kd/K与计算结果中的计算长度系数可知，随着Kd/K的减小，计算长度系数相应增大。

(2)在高低墩组合中，由于低墩抗推刚度较大，使得高墩墩顶的弹性约束刚度增大，从而计算长度系数偏小;而由于高墩偏柔，使得低墩墩顶的弹性约束刚度偏小，从而计算长度系数偏大。在高墩组合中，由于墩高相差不大，墩顶弹性约束刚度接近，使得桥墩的计算长度系数接近。因此，桥梁结构整体布置时，对位于陡峭岸坡墩高相差较大的桥跨组合中，应避免由于矮墩刚度偏大，造成桥梁结构局部内力偏大，在保证强度和稳定性的前提下，应尽量使低墩偏柔，使桥梁结构整体刚度均匀、受力合理。