基于格子Boltzmann方法的多相态流动模型研究

范 俊

(西北工业大学航空学院流体力学系，西安710072)

近20年里，格子Boltzmann方法(lattice Boltzmann method，LBM)在理论与应用研究上取得了显著的进展，并逐渐成为相关领域的研究热点.与基于宏观Navier－Stokes(N－S)方程组的传统计算流体力学方法不同，格子Boltzmann方法是一种介观方法［1－2］.

以动理学模型为基础的介观方法，既具有微观方法假设条件较少的特点，又具有宏观方法不关心分子运动细节的优势.因此在处理多尺度、多物理的复杂流动问题中，介观方法具有较大优势和潜力.格子Boltzmann方法是由格子气自动机(lattice gas automata，LGA)发展而来的，是一种不同于传统数值方法的流体计算和建模方法，其主要优点有:演化过程物理清晰，边界条件容易处理，计算简单，容易编程实现，并且计算是局部的，具有良好的并行性和扩展性，有利于大规模流动问题的计算.该方法在宏观上是离散方法，在微观上是连续方法.在许多传统数值方法难以胜任的领域，如多相多质流、微/纳米尺度流、多孔介质流、非牛顿流体、磁流体、生物流体粒子悬浮流、湍流、化学反应流、燃烧问题、晶体生长等，格子Boltzmann方法都取得了成功的应用，并揭示了多种复杂现象的机理，推动了相关科学的发展［3］.

1988年，McNamara和Zanetti提出了第一篇关于格子Boltzmann方法的论文，出现了最早的格子Boltzmann模型，但仍沿用格子气自动机的碰撞方式，具有计算指数复杂性.1991到1992年，几个研究小组分别独立提出了一种更简单的模型，即流行的单松弛(Single Relaxation Time，SRT)模型，又被称为 LBGK(lattice Bhatnagar－Gross－Krook)模型［4－5］.LBGK 模型极大地简化了计算量，并且在一定条件下可以还原出正确的Navier－Stokes方程组，有效地克服了格子气自动机的不足.同时期，法国学者D·d’Humières提出了更一般性的广义多松弛时间(multiple－relaxation－time，MRT)模型［6］.2000 年，P·Lallemand和 Luo对 MRT 模型做了细致的理论分析，研究表明其在物理原理、参数选取和数值稳定性方面都有很大的优势.

多相态流体是包含明显分界面的流体系统，自然界和现实工程中的流体系统或多或少地包含了其它物质，完全单相态单组份的流体是几乎不存在的.多相态流动是化工、能源、航空、航天、航海、生命科学等领域广泛存在的流动现象.在LBM发展的过程中，很多研究人员提出了各种基于LBM的应用方案，有几种多相态流体模型，分别是颜色模型［7］、伪势模型［8－9］、自由能模型［10］、动理学模型.其中的伪势模型是Shan和Chen于1993年提出的刻画粒子间相互作用力的LBM模型，利用一种伪势函数来反映粒子间相互作用.当选择了正确的伪势函数，粒子间相互作用力保证了多相态分离流动的自动发生.

对于传统的LBM模型，Boltzmann方程中的外力项离散与引入是一个关注热点与难题.对于多相态流动，正确地引入与处理外力项是非常重要.因为这对数值精度和计算稳定性有显著的影响.本文采用了LBGK模型和MRT模型，结合伪势模型和三种不同的外力模型，模拟多相态流体的分离流动现象，并对比不同数值模型的粒子间相互作用强度范围和伪速度情况.

1 数值方法

1.1 格子Boltzmann方法

完整的LBM模型通常由格子(即离散速度模型)、平衡态粒子分布函数和演化方程三部分组成.首先，LBM输运方程的基本演化形式为

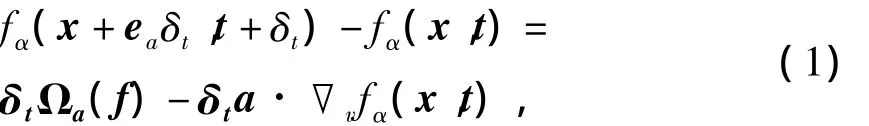
其中:fα(x，t)是t时刻在x位置处以离散速度eα运动的粒子分布函数，表示的是该状态下的粒子的统计学概率;a为外力引起的加速度，Ωα(f)为表示粒子间碰撞引起的变化量的碰撞算子.求解Boltzmann方程最主要的难点在于碰撞项Ωα(f)的处理，它是关于粒子分布函数的非线性积分.因此，通常的想法是考虑能否用简化近似形式代替原本的碰撞项，这是LBM模型分类的依据.LBGK模型和MRT模型都采用线性碰撞算子处理，LBGK模型只有一个自由参数，与运动黏性系数相关，体黏性与运动黏性固定相关;而MRT模型将LBM方程发展至矩空间中处理，形式更复杂，但可调节的自由参数更丰富，其中包括了体黏性系数.两种模型碰撞算子的细节可以在很多已发表的文献中得到，松弛时间参数与运动黏性系数的关系式为

其中:τ是松弛时间参数，v为运动黏性系数，δt为时间步长，cs是与格子模型有关的格子声速.

图1 D2Q9不可压格子模型离散速度图

1992年，Qian等人提出了目前流行的DdQm系列格子模型［11］，d代表的是空间维数，m代表的是离散速度个数，对应的平衡态粒子分布函数形式如下

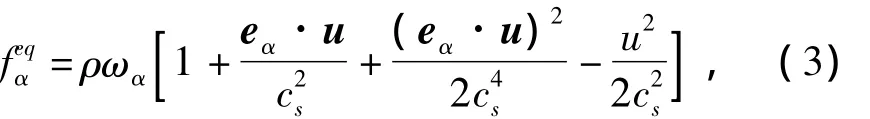
其中:ωα是与格子模型有关的权系数.本文采用的D2Q9是最常用的二维不可压格子模型，如图1所示，定义式为

其中:c=δx/δt，δx为格子步长.对于 D2Q9 格子模型，权系数 ωα的设置为 w0=4/9，w1，2，3，4=1/9，=1/36，格子声速 cs为格点处的宏观物理量的计算，可通过将粒子分布函数求离散速度矩得到，不考虑外力作用的情况下，

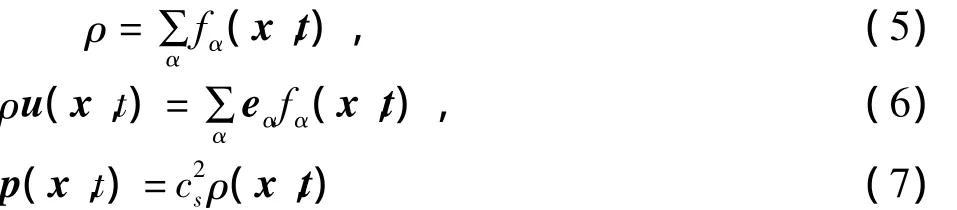
LBM模型三要素中的演化方程可分解为两个步骤进行计算:

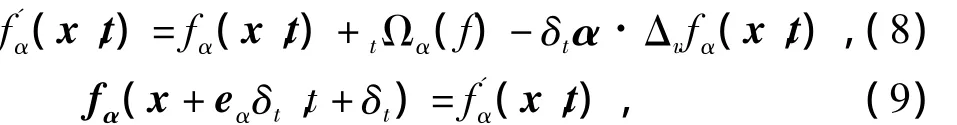
其中:式(8)是碰撞步，式(9)是迁移步.从上式可以看出，碰撞步骤的计算是在当前格点处局部进行的，迁移步骤只与相邻的格点有关，这体现出LBM良好的计算局部性和优秀的并行计算适用性.

在LBM模型中，外力项 a·▽vfα(x，t)无法直接应用求解.在Shan和Chen的原始模型中，通过改变平衡态粒子分布函数的宏观速度实现外力作用的影响，平衡态宏观速度为

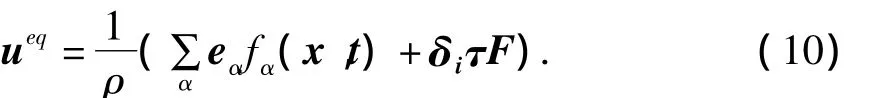
从式(10)可以发现，相同的粒子间相互作用力下，随着松弛时间参数的改变，平衡态宏观速度是不一样的，这样的影响将会在后面的算例结果与分析中得到验证.

郭照立等人对LBM方程中的外力项进行研究并提出了一种二阶矩处理模型，应用到了MRT模型上［2］:

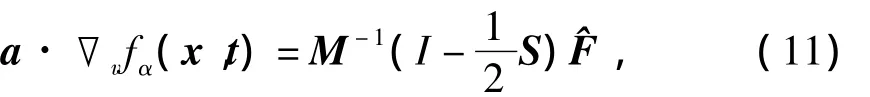
其中:M－1是MRT模型的逆变换矩阵，S是包含了多松弛时间参数的对角矩阵，^F是作用力的各个速度矩，定义为

Kupershtokh等人［12］提出了一种精度较高、稳定性和通用性较优秀的外力模型，也是通过平衡态粒子分布函数实现外力作用的影响.然而，他们的外力模型和郭照立等人的类似，在碰撞算子以外处理，由于是基于平衡态粒子分布函数，该外力模型可适用于不同的碰撞算子:

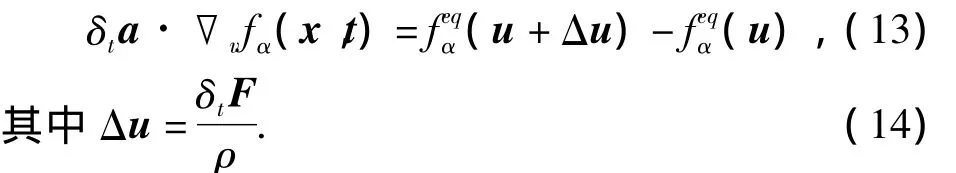
上文介绍到的三种外力模型，分别采取三条完全不同的思路以实现外力项在离散Boltzmann方程中的引入，然而在外力作用的影响下，三种外力模型的流体宏观速度同时都是取为碰撞前速度与碰撞后速度的平均值:

1.2 伪势模型

Shan和Chen提出的伪势模型，又被简称为SC模型.他们提出了一种伪势函数Ψ(x，t)来表示粒子间相互作用，伪势函数与当地密度有关，而粒子间相互作用力是基于伪势函数求得:

其中:G是一个表示粒子间相互作用强度的参数.从公式(16)可以发现，粒子间相互作用力是对离格点处最近和较近位置上的粒子相互作用势求和.本文采用的伪势函数为Shan和Chen所提出的最原始方程:

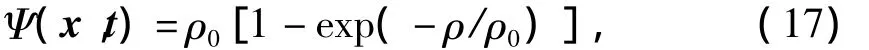
其中:ρ0是一个自由参数.

代入式(16)和(17)，流体系统会得到一个非理想状态方程:

2 数值结果与分析

伪势模型的一个优点在于多相态流体的分离流动自动发生，不需要其他传统 CFD方法(如VOF、Level Set)所用到的动态重构、界面追踪等技术，而且它们还难以捕捉跟踪大量细小、分散的相界面.为了测试多相态流体的平衡特性，本文对多相态流体的分离流动进行数值模拟，分别选取了不同的相互作用强度G和运动黏性系数v.

整个数值模拟是在周期边界和一套密度为128×128的笛卡尔网格下完成，流场平衡态的数据结果统一在500 000迭代时间步后获取.初始化流场速度为0，流场各格点密度为一个固定值加上一个格点处随机波动，该随机波动是流体由于周围相互作用力的不平衡而自动发生分离流动的原因.对于MRT模型，除了与运动黏性系数相关的松弛时间参数，还有多个自由松弛时间参数需要确定，本文对它们的定义如下［13］.

sα=(1，0.7，1.5，1，0.8，1，0.8，1/τ，1/τ).

图2所展示的是粒子间相互作用强度为－5时，两相态流体的分离流动过程的密度分布截图，时间步分别等于 200、800、1 600、1 800、4 000、20 000.在图2(A)可以清晰地看到前期大量细小、分散相界面的存在，随着时间步的推进，液滴不停地融合，最后形成一个稳定平衡的大液滴.

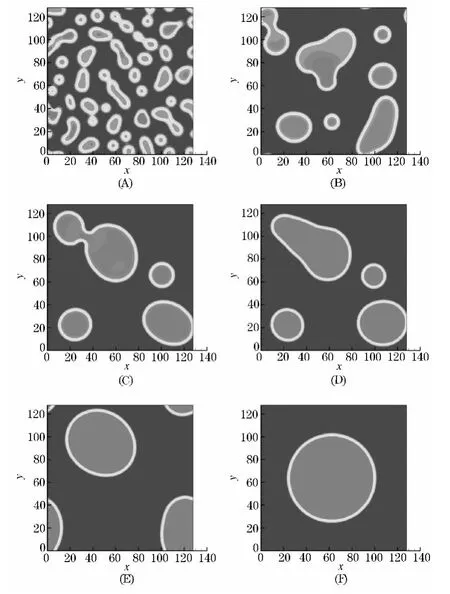
图2 两相态流体分离过程，粒子间相互作用强度

如上文所提到，LBGK模型的体黏性与运动黏性固定相关，两者相等，由于稳定性问题，这限制了LBGK模型在运动黏性较小(或雷诺数较高)的应用.从图3中可以看到，即使固定了运动黏性系数，MRT模型对粒子间相互作用强度的适用范围比LBGK模型的更广，这意味着更大的密度比，在图4中得到了验证.我们曾尝试在LBGK模型上采用郭照立和A·L·Kupershtokh的外力模型，效果仍不理想，MRT模型的上限是5.75，而LBGK模型的上限是 5.25.

伪速度，是数值模拟中多相态流动平衡状态下的最大流场速度，一般都表现为相界面附近的旋涡流动，这是一种不健康的非物理现象.伴随着伪密度振荡的发生，过大的伪速度会降低数值精度和影响计算稳定性，极大地限制了模型的应用范围.因此，伪速度经常作为多相态流动数值模拟的评判标准和对比依据.图5展示的是两种外力模型的伪速度随粒子间相互作用强度变化的曲线，两种外力模型的结果差异不大，随着密度比的增大而单调递增.

图3 不同模型下的液相态和气相态密度随粒子间相互作用强度变化曲线

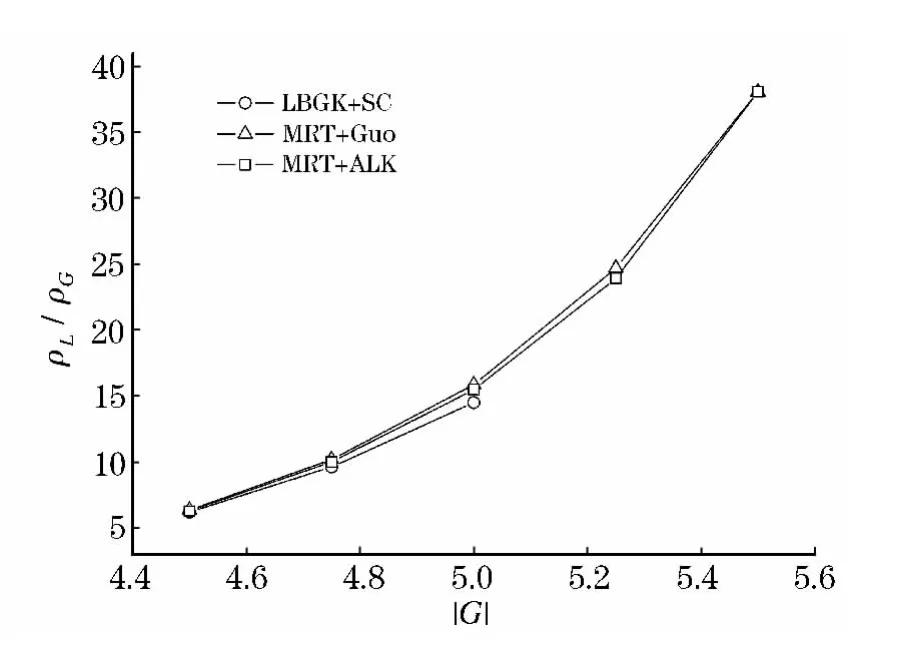
图4 不同模型下的液相态和气相态之间密度比随粒子间相互作用强度变化曲线

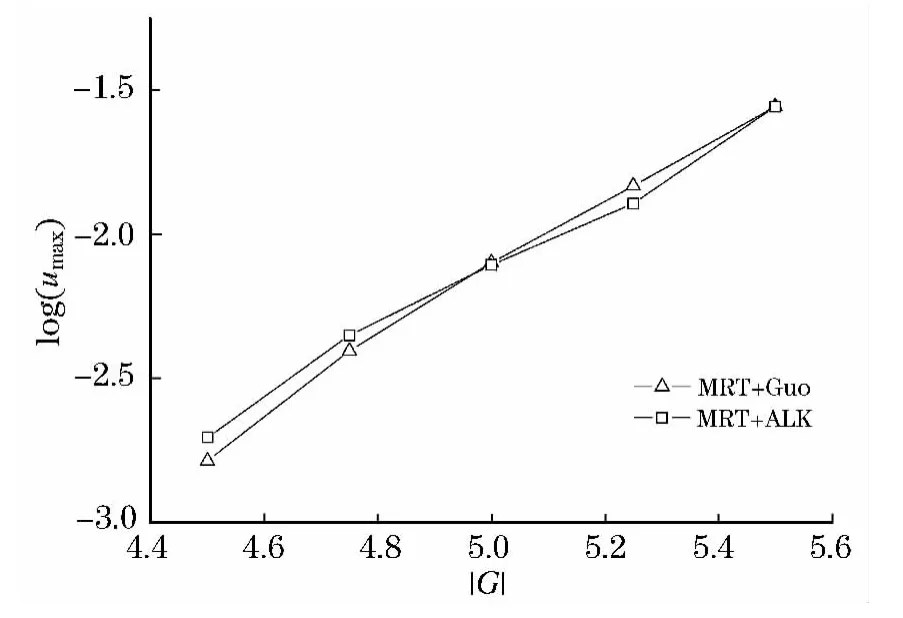
图5 不同外力模型的伪速度随粒子间相互作用强度变化曲线

SC模型的外力模型对粒子间相互作用力的引入受松弛时间参数的影响，即不同的运动黏性系数下，多相态流体平衡特性可能会不相同.因此，本文进行了一系列的测试.三种数值架构的粒子间相互作用力都是按照式(16)计算，在图6中，LBGK模型的平衡态密度特性随着运动黏性系数的变化而改变，这一种现象在一些已发表的文献中曾被提到［13－14］，在图7中的平衡态密度比曲线的变化表现得更明显.由于外力的引入方式不合理而导致的这一种现象是不受欢迎的，这不利于应用过程中对平衡态特性的设定.另一方面，从理论上，通过多尺度展开(Chapman－Enskog分析)，加入了外力模型的LBM方程可还原为传统的宏观N－S方程组:

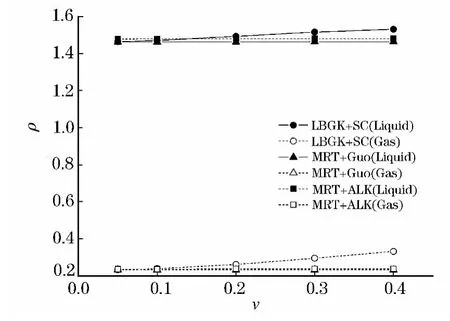
图6 不同模型下的液相态和气相态密度随运动黏性系数变化曲线

其中:Rρ和Rv分别是质量方程和动量方程偏差量.SC外力模型存在因引入外力而导致的偏差量，这一方法主要适用于外力为常数的情况，而郭照立和A·L·Kupershtokh的偏差量为0，完全满足宏观方程的还原.

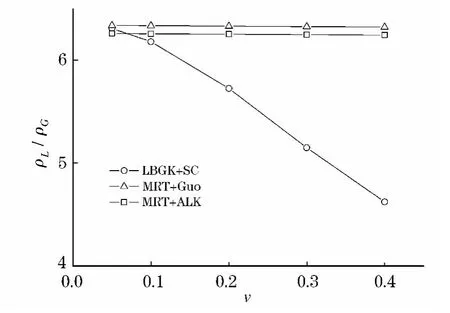
图7 不同模型下的液相态和气相态之间密度比随运动黏性系数变化曲线

3 结语

本文采用LBGK模型和MRT模型，结合三种外力模型对多相态流体的分离流动进行数值模拟.不同的粒子间相互作用强度和运动黏性系数下的测试，证明了LBGK模型对多相态流动模拟在数值精度与精算稳定性上的局限;MRT模型能够模拟更大密度比的流动;同时更合理的外力模型能够改善MRT模型在多相态流动的平衡态特性，避免受到运动黏性系数变化的影响，可以更方便地设定多相态流体的平衡特性.最后，这两种不同的外力模型的数值结果没有表现出明显的优劣差异，也都能成功地还原到对应的宏观N－S方程.

［1］何雅玲，王 勇，李 庆.格子Boltzmann方法的理论及应用［M］.北京:科学出版社，2009.

［2］郭照立，郑楚光.格子Boltzmann方法的原理及应用［M］.北京:科学出版社，2009.

［3］AIDUN C K，CLAUSEN J R.Lattice－Boltzmann method for complex flows［J］.Annual Review of Fluid Mechanics，2010，42:439–472.

［4］CHEN S，CHEN H，MARTINEZ D，etal.Lattice Boltzmann model for simulation of magneto － hydrodynamics［J］.Physical Review Letters，1991，67(27):3776–3779.

［5］QIAN Y H，D’HUMI RES D，LALLEMAND P.Lattice BGK models for Navier － Stokes equation［J］.Europhysics Letters，1992，17(6):479–484.

［6］D’HUMI RESD.Generalized lattice Boltzmann equations［J］.Rarefied Gas Dynamics:Theory and Simulations，1994，159:450–458.

［7］GUNSTENSEN A K，ROTHMAN D H，ZALESKI S，etal.Lat-tice Boltzmann model of immiscible fluids［J］.Physical Review A，1991，43(8):4320.

［8］SHAN X W，CHEN H D.Lattice Boltzmann model for simulating flows with multiple phases and components［J］.Physical Review E，1993，47(3):1815.

［9］SHAN X W，CHEN H D.Simulation of nonideal gases and liquid － gas phase transitions by the lattice Boltzmann equation［J］.Physical Review E，1994，49(4):2941.

［10］SWIFT M R，ORLANDINI E，OSBORN W R，etal.Lattice Boltzmann simulations of liquid－gas and binary fluid systems［J］.Physical Review E，1996，54(5):5041.

［11］QIAN Y H，D’HUMI RESD，LALLEMAND P.Lattice BGK models for Navier－ Stokes equation［J］.Europhysics Letters，1992，17(6):479–484.

［12］KUPERSHTOKH A L，MEDVEDEV D A，KARPOV D I.On equations of state in a lattice Boltzmann method［J］.Computers＆ Mathematics with Applications，2009，58(5):965－974.

［13］YU Z，FAN L S.Multirelaxation－time interaction－potential－based lattice Boltzmann model for two－ phase flow［J］.Physical Review E，2010，82(4):046708.

［14］HE X，SHAN X，DOOLEN G D.Discrete Boltzmann equation model for nonideal gases［J］.Physical Review E，1998，57(1):13－16.