低复杂度高度场的通视性研究及快速光照计算

李 华, 杨华民, 赵建平

(长春理工大学 计算机科学技术学院, 长春 130022)

0 引 言

高度场也称2～1/2维表面, 在地理信息、 模拟仿真和3D游戏等方面有广泛的应用。近些年, 高度场的实时高真实感绘制已成为计算机图形学和虚拟现实研究重点之一。在交互可视化时, 高度场互见性的计算需要判断每一点对场景内其他所有点的可见性, 计算量大, 有局限性, 基于物理特性的可见性判断更加复杂。在军事、 通讯等方面高度场的通视性检测及应用也非常广泛。通过对高度场场景模型增加光照和阴影效果, 为视觉观察提供了关键线索。如高大的建筑物或山峰离地面的高度和几何关系等。

高度场正确的物理关系绘制和模拟, 主要依靠判断场景点间的遮挡关系。在真实感渲染技术中, 可见性算法主要有两方面应用： 几何面的剔除和光照计算。前者用于加速渲染管线的计算效率, 后者用于确定场景表面点的亮度。一般情况下, 场景中任意一点都可作为光源影响其他场景点, 因此, 全局光照要考虑场景内每一点接收所有光源的光照, 计算量相当巨大。在静态几何体光照计算中可通过预计算的方式预先确定可见面片, 以降低计算复杂性, 但对动态场景的几何体的计算却是个复杂问题。因为每帧画面随着相对位置发生变化, 可见性的判断需要重新进行, 这大大增加了计算复杂性和成本。

1 高度场可见性

高度场可见性判别需计算来自各个方向上的顶点的遮挡关系。MAX[1]利用各方向的水平轮廓信息构造地平线地图, 实现凸凹映射表面的硬阴影计算, 该算法已应用于静态高度场的实时绘制中。近些年, 学者们提出了一些实时动态的高度场计算的方法, 通过采样高度场在各个方向角上的顶点信息, 找到主要的遮蔽体, 进而获得近似软硬阴影[2,3]。对于一个尺寸为N×N的高度场地图, 如果一个方位角方向的所有高度场点都被认为是接收点, 计算的时间复杂度将达到O(N3)。为降低计算复杂性, 对不同方向角以不同采样分辨率采样, 可以适应场景的不同复杂度, 但仅适合于近似计算软阴影效果,而不能实现高分辨率的高度场场景计算。Ville等[4]提出沿方位角方向利用相邻采样点之间的一致性关系, 计算高度场在任何给定的方向上所有点的视界角, 可以把计算复杂性降为O(N2)。Dimitrov等[5]提出将阴影图中的深度缓冲区信息作为高度场信息, 近似计算环境光遮蔽。由于深度缓冲区的信息是几何可见性信息的子集, 所以, 这些方法只能通过抽样计算局部近似遮挡关系, 这种近似计算, 适合于扩展到计算屏幕空间的环境光遮蔽的直接光照和间接光照计算。

低复杂度高度场由于其特殊的形式, 使可见点的数量相对于场景点的数量大大减少,Ville[6]研究了地形、 砖墙表面、 网格以及街区块模型4种高度场图(见图1)在某个方向角的可见比例, 对于一个1 0242的高度场图, 沿其中一个方向的可见度比例最大为5.6%, 最小为1.1%。足以计算半镜面反射及自发光表面的光照效果。凸包树的构建、 存储和搜索效率较低, 确定一种简化的可见点查找和存储结构, 将能大大提高通视性判断和光照计算效率。

a 地形 b 砖墙表面 c 网格 d 街区块模型

2 凸包树策略及转化

图2 扫描方向示意图

场景剖面扫描可以用一棵树的形式表述, 如图3所示。该存储结构记录了高度场中每个场景点的方向可见点, 且水平高度角度最大的可见点在凸包树中深度即该点的方向视界边界。笔者依据该思想, 提出一个基于凸包树搜索的可见性判别算法, 建立基于顶点的可见性二叉树并进行线索化, 作为高度场的光照计算依据, 当光源及视角位置变化时, 通过快速查找可见性树表索引获得遮挡信息。

2.1 线性扫描

图3 高度场剖面图

高度场数据是以网格形式给出的, 即对于N×N高度场中一点(x,y)为平面坐标,z为高度值, 该算法的输入数据为顶点坐标和高度。观察点或光源的位置任意, 因此, 需要对场景中每一点确定其可见范围。沿着某一方向扫描高度场地图, 能在线性的时间内获得水平高度角信息, 进而判断可见片段。

由于高度场数据受到其特殊属性的限制(见图3), 扫描线将2.5维信息降解成1.5维切片。

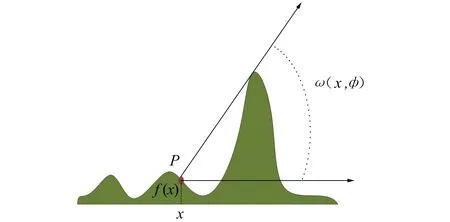
图4 方位角度接收点x的水平高度角

2.2 水平方位角计算

在3D场景内, 要确定表面一点P=(x,y,f(x,y))的可见范围, 需要已知P点在各个方向上的水平高度角。φ方向上的参数化坐标值为(cosφ,sinφ), 其中φ∈[0,2π]。可见性被表示为P从地平线达到最大仰角, 叫φ方向水平高度角, 也称为视界角[5]。设任一点p(x,f(x))φ方向的视界角为ω(x,φ), 在高度角小于ω的位置, 被遮挡而无法看到更远处(见图4)。

ω(x,φ)定义为

(1)

其中t表示沿着φ方向远离x点的水平距离, 反正弦函数是单调函数。视界角ω如果为0, 表面本身没有任何遮挡,ω大于π/2时被自身遮挡。

2.3 凸包遍历树

高度值相邻的两个点中, 只有当Pi+1的高度大于Pi时,Pi+1才可见。因此, 扫描遍历所有t∈(0,∞)才是最有效的方法, 遍历树如图5所示。

图5 凸包树

2.4 凸包树搜索及可见性二叉树

凸包树搜索及流程如图6所示。

图6 凸包树搜索流程图

凸包树型结构转化成对应的可见性二叉树及线索化, 可以提高搜索速度。该二叉树以扫描起始顶点为根节点P0, 加入新的顶点P1, 计算新顶点P1的水平方向角β1, 加入新顶点P2, 连接顶点P2的水平方向角β2, 若β2>β1, 则更新当前最大水平方向角Max, 同时P2可见, 若β2<β1, 则P2对P0不可见。不可见以后若出现再次大于最大水平方向角的新顶点Pi, 则Pi对应片段为可见体。依次类推, 最终完成可见性二叉树搜索。 从扫描起点, 每条扫描线对应一个二叉树存储表, 用来检索可见顶点。由于通视性具有相互性, 所以为了便于反向扫描, 需将二叉树先序线索化, 以便查找双亲节点。该结构实现了从场景点内任一点观察, 周围高度场的可见性信息均可从可见性二叉树进行查询。

高度场的互见性应用范围广泛, 如, 通信节点或卫星的覆盖范围及最佳位置判断、 虚拟场景真实感绘制和3D场景的交互式应用等。为了验证互见性判断效果, 笔者模拟高度场的全局光照的计算, 忽略一次间接光照的可见性判断, 实现高度场的光照效果绘制。

3 高度场光照及阴影计算

高度场数据图的光照效果主要是自阴影和间接光照, 为快速计算可接受的模拟效果, 忽略间接光照的遮挡关系[7], 场景的直接光照通过渲染方程实现。场景内一点P的光照强度L0的计算可表示为

(2)

在点光源情况下,

L0(p,ω)=fr(p,ω,p→L)Le(L,L→p)G(p,L)V(p,L)

(3)

若场景中任意两点的可见性已知, 则问题的关键即可解决。笔者结合阴影图实现动态低复杂度高度场的阴影计算和近似光照效果。高度场的数据存储在N×N的二维数组中, 对于点X(x,y,z),N×N的二维数组确定位置(x,y), 其z值为高度值, 从光源视角位置计算光源到场景中每一点的深度, 根据交点坐标与各可见点确定光照可见点。高度场标量函数f(x)=f(x,y), 对于3D场景内一点p(x,y,f(x,y))的软阴影计算, 需要计算p点所有方向上可见点ρ, 最终p点的亮度由各可见点累加获得

Lp=∑ρ

(4)

4 实验效果

该实验环境为处理器Intel(R)Xeon(R) CPU E5620@双核2.40 GHz, 显卡NVIDIA Quadro 4000。绘制的高度场模型如图7所示, 场景帧率如表1所示。

a 圆锥1 b 圆锥2 c 圆锥3

d 山峰1 e 山峰2 f 山峰3

表1 场景帧率

5 结 语

笔者通过线性扫描并存储方位角信息, 可以快速获得可见高度场顶点, 运用在阴影图中进行低分辨率采样, 该实验实现了近似高度场绘制的交互式帧率, 对动态场景和交互式应用提供了依据和保障。从表1可以看出, 在动态光源下, 高度场的绘制达到交互式帧率, 实现了对地复杂度高度场的可见性判断, 并形成光照及阴影。

真实感绘制随着GPU技术和并行编程的发展, 在今后的工作中将对线性扫描的并行化改进及基于CPU-GPU的异构编程将做进一步研究。

参考文献：

[1]MAX N: Horizon Mapping: Shadows for Bump-Mappedsurfaces [J]. The Visual Computer, 1988, 4(2): 109-117.

[2]SNYDER J, NOWROUZEZAHRAI D. Fast Soft Shadows on Height Fields via Multi-Resolution Image Processing. Tech Rep MSR-TR-2008-77, Microsoft Corporation [EB/OL]. (2013-05-17). http:∥researh.microsoft.com/apps/pubs/default.aspx?id=70587.

[3]NOWROUZEZAHRAI D, SNYDER J. Fast Global Illumination on Dyna Height Fields [J]. Computer Graphics Forum: Eurographics Symposium on Rendering, 2009, 28(4): 1131-1139.

[4]VILLE TIMONEN, JANWESTERHOLM. Scalable Height Field Self-Shadowing [J]. Computer Graphics Forum, 2010, 29 (2): 723-731.

[5]DIMITROV R, BAVOIL L, SAINZ M. Horizon-Split Ambient Occlusion [C]∥SI3D’08: Proceedings of the 2008 Symposium on Interactive 3D Graphics and Games (2008). New York, NY, USA: ACM, 2008: 178-192.

[6]VILLE TIMONEN. Low-Complexity Intervisibility in Height Fields [C]∥Computer Graphics Forum (Volume 0) 2012, 36(2): 1-14.

[7]DACHSBACHER C, STAMMINGER M. Reflective Shadow Maps [C]∥Proceedings of the 2005 Symposium on Interactive 3D Graphics and Games. New York, NY, USA: ACM Press, 2005: 203-231.