基于Procrustes均值形状和Fan-Beam变换的步态识别

侯一民，刘 凤

(东北电力大学 自动化工程学院，吉林 132012）

0 引言

生物识别技术是基于人体独特生物特性的身份辨识方法。物理上的生物识别技术，如人脸、虹膜和指纹的识别一般需要在规定的角度下进行，如身体接触或是接近[1]。目前步态识别的技术大致可分为两类：一是提取步态轮廓静态的特征，如Huang 等人[2]提出的用平均轮廓图像作为步态特征进行识别。这种方法使得信息的损失比较大。文献[3]采用Procrustes形状分析的方法，但该方法丢失大量动态信息。二是利用轮廓的动态特征，如基于步态能量图和二维主成分分析的步态识别方法[4]，但是穿着对步态能量图影响比较大。Zhang[5]提出基于主动能量图及二维局部投影的识别方法保留了更多的动态信息，但AEI是由步态视频帧差图像叠加组成，受视角限制。Procrustes均值形状特征包含更多静态信息，而基于步态能量图的Fan-Beam变换可以得到更多的频率动态特征，本文主要尝试将两种特征结合起来提高多角度的步态识别率。

1 步态周期检测

首先以步态轮廓的宽高比作为步态周期检测的依据。图1(a)为一组步态图像序列，图1(b)为用步态轮廓的宽高比对这一图像序列检测出的结果。从图1可以看出，一个步态周期约有24个步态序列图像。

图1 步态周期检测

2 不同步态特征提取

2.1 Procrustes 均值形状特征提取

首先用质心计算公式(1)来求出轮廓的质心。然后对轮廓进行等角度采样，得到N个采样点。

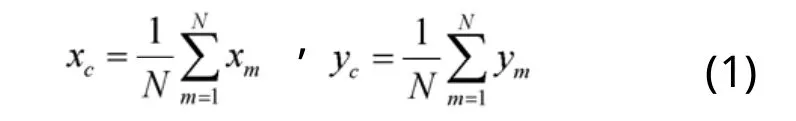
式中，N为边缘像素点个数，(x，y)为边缘点的直角坐标。

一帧步态图像在采样后，得到能够表达这个轮廓的一维向量。将每一个轮廓对应的复数向量称为配置向量：U=[u1u2…uN]T。式中，ui=xi+yi，(xi，yi)是采样点的坐标。每一个轮廓都对应一个配置向量Ui (i=1，2…，n) ，n是一个步态周期的帧数。然后计算配置矩阵S，S的计算公式如式(2)：

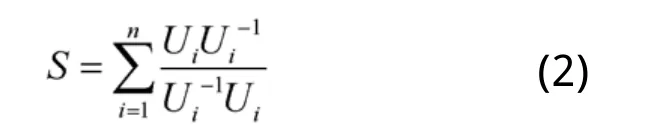
S的最优配置向量即S的最大特征值对应的特征向量即为Procrustes 的均值形状 。图2分别为同一运动目标不同序列图像和不同视角下2个运动目标的Procrustes 均值形状的对比。

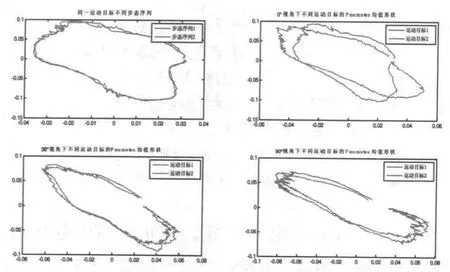
图2 Procrustes 的均值形状分析

从图2中可以看出，同一运动目标的Procrustes均值形状是相似的；相同视角下的不同运动目标的Procrustes 均值形状是不同的，而且Procrustes 均值形状适用于非单一性视角的步态识别。

2.2 步态能量图(GEI)及Fan-Beam变换

2.2.1 步态能量图(GEI)及 Fan-Beam变换

若一组步态周期图像序列为At(x，y)，用公式(3)来计算步态能量图：

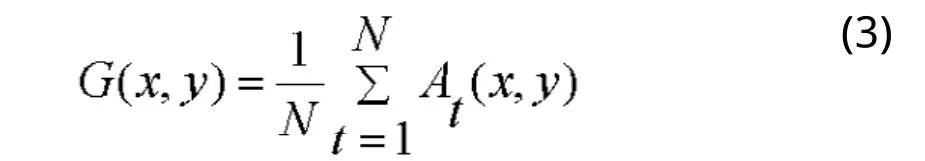
式中，N为一个步态周期序列的总帧数，t为步态序列帧数，(x，y)为二值图像像素坐标。图3(a)为一个步态周期的序列图像，图3(b)为按照公式(3)计算出的图3(a)步态能量图(GEI)。

图3 步态能量图（GEI）

Radon变换[6]用来计算图像矩阵在某方向上的投影，它保留了更多的步态能量图的频率信息。Radon变换的计算公式如式(4)：

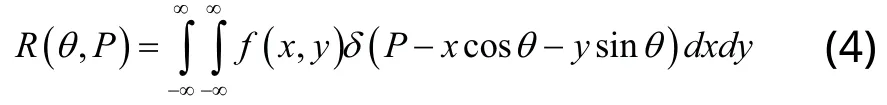
式中， 为点(x，y)的极角，P为点(x，y)的极径， 为脉冲响应函数。

Fan-Beam变换[7]就是对扇形数据的Radon变换。如图4所示为步态能量图(GEI)的Fan-Beam映射结果。

图4 Fan-Beam变换

2.2.2 二维主成分分析

若一个大小为m × n 的图像A，投影矩阵(即投影轴)为X∈Rn×d(n≥d)，Y是A对应到X方向上投影，投影特征向量为Y。如公式(5)：

寻找最优投影轴X使投影影本的可分离程度最大。用投影特征向量的总体散布矩阵作为准则函数J(X)，公式如式(6)：

式中，SY为训练样本投影特征向量Y的协方差矩阵，trSY为SY的迹。协方差矩阵SY的表示如公式(7)：

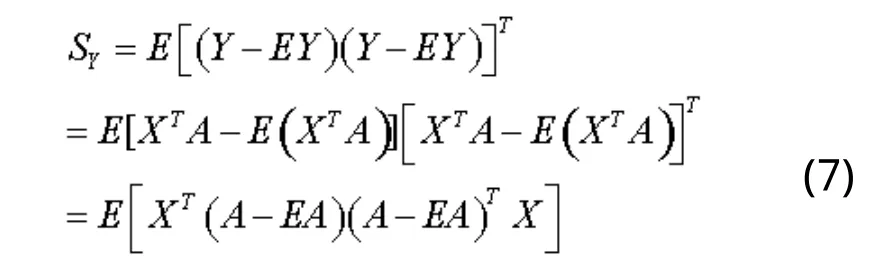
矩阵迹可表示为公式(8)：

图像A的协方差矩阵为G，计算公式如式(9)：

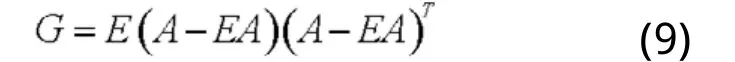
假设有M幅测试样本AK，那么可以按公式(10)估算G：

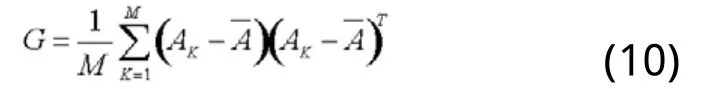
所以式(6)的准则可表示为式(12)：

最优投影轴即为图像总体散布矩阵的最大特征值的特征向量。要选择一组标准正交投影轴x1，…，xd，实际上也是G的前d个最大特征值对应的特征向量，满足公式(13)、(14)：

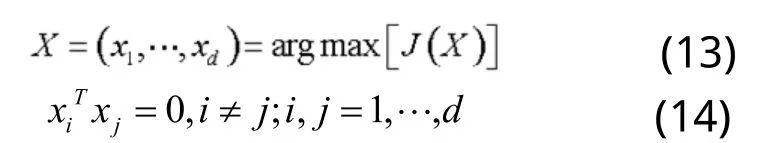
用获得的投影矩阵X，根据公式(5)就可以得到一组特征向量Y1，Y2，…，Yd作为图像A的m xd维的特征矩阵。

3 特征融合及识别

分别计算出两个特征的测试样本和训练样本之间的欧式距离D(Rp，Ri) 和D(Sp，Si)，(i=1，2，…，c)，c为样本数目。然后用融合函数D把两者识别结果融合起来，融合函数D的计算公式如下：

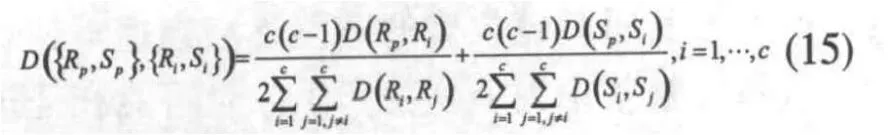
最后用公式(16)判别，如果满足公式(16)，那么测试样本P∈Wk：

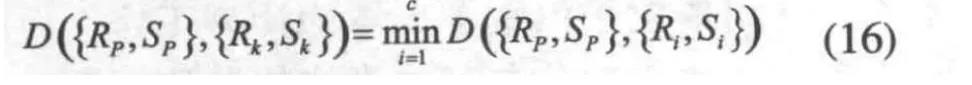
4 实验步骤及结果分析

中国科学院自动化所的CASIA B大规模步态数据库，该库共有124人，每个人分别有11个视角。整体算法流程如图5所示。

图5 步态识别算法流程图

本文依据上述基于特征融合的方法分别选取0°，36°，90°三个角度的正常行走步态序列做为第一组实验Set A，3组正常行走的步态序列作为训练样本，另外3组作为测试样本；选取背包行走步态序列做为第二组实验Set B，1组作为训练样本，另外1组作为测试样本；选取穿大衣行走步态序列做为第三组实验Set C。实验过程如下：

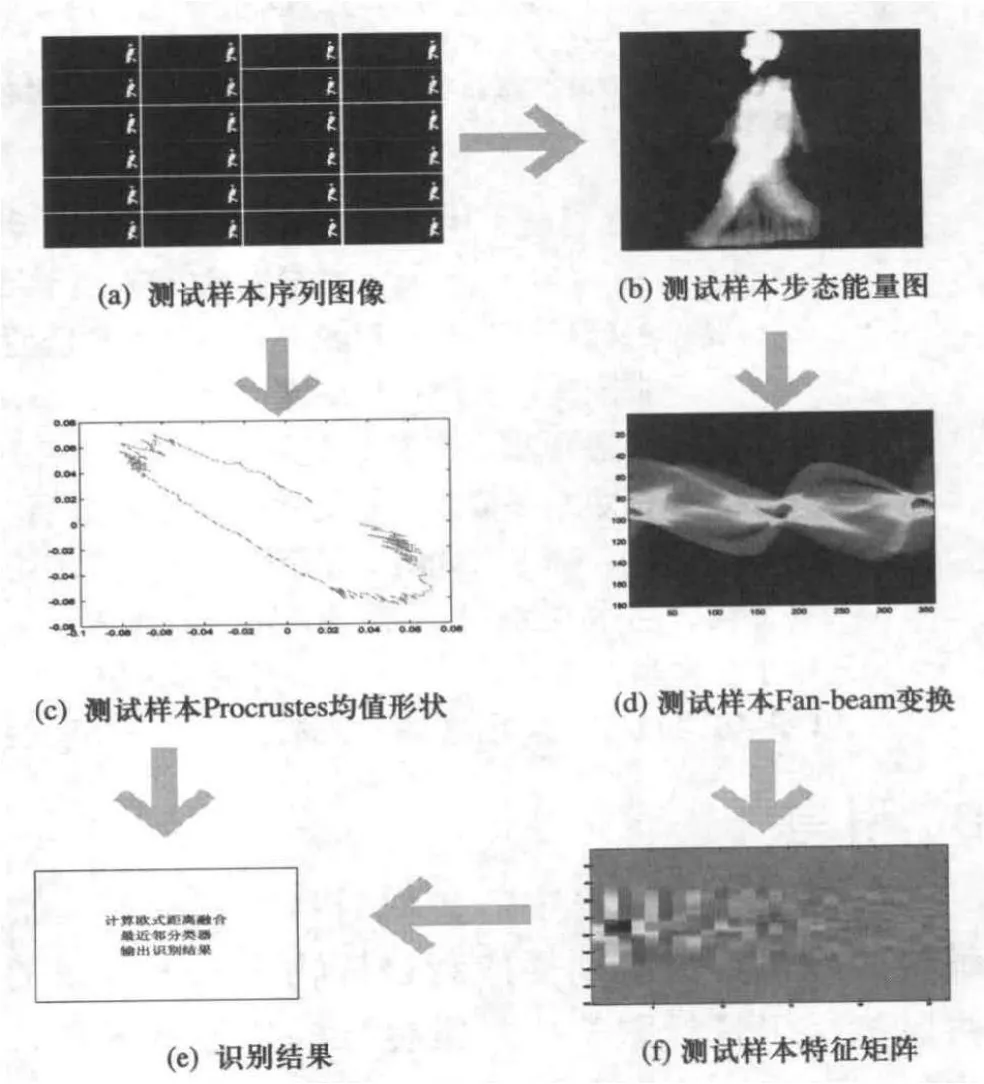
图6 测试过程及结果

实验结果如图7所示。

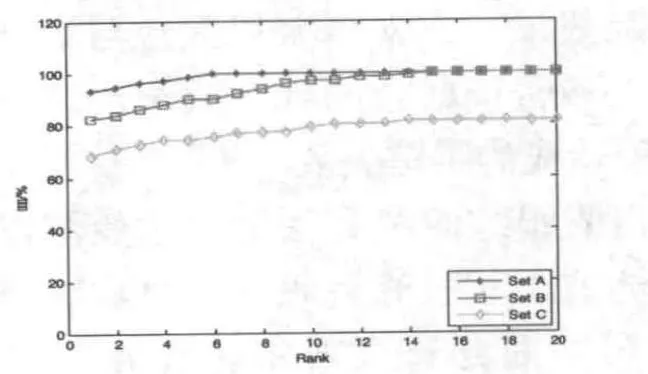
图7 实验结果

从图中可以看出正常行走的步态序列识别率较高，三个角度平均识别率达到93.14%。因为它所包括的形状信息更为准确，遮挡较少。而在背包和穿大衣的情况下，步态特征的提取受到了噪声影响，识别率相对较低。

为了验证本文所提出的算法的有效性，又分别选取0°，36°，90°三个角度的正常行走的步态序列与其他三种方法对比，分别为PM S、GEI+2DPCA[4]和Radon+2DPCA[8]实验结果见表1。(15)

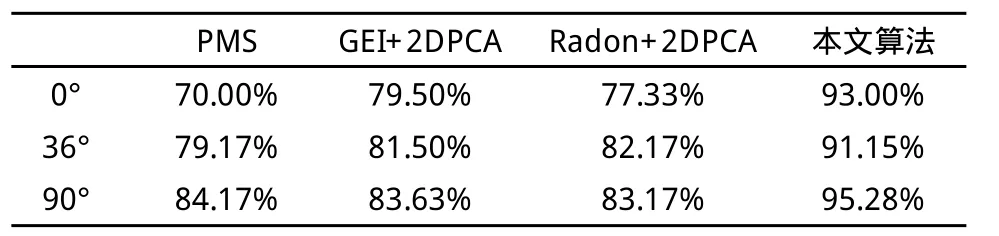
表1 在3个视角下4种不同算法的正确识别率

由对比试验可见，通过特征融合提高了步态识别率，明显高于基于单个特征的步态识别算法，说明Procrustes均值形状和基于GEI的Fan-Beam变换相结合的方法包含的步态特征更全面，达到了比较理想的识别效果。

5 结论

本文先提取基于统计分析方法的步态序列的Procrustes均值形状信息，包含了步态大量的形状特征，相对遗漏信息较少；然后提取步态能量图(GEI)的Fan-Beam变换频率动态特征，并用二维主成分分析降维，再将两者结合起来进行分类识别。实验结果表明该方法比提取单一的静态特征或动态特征的识别方法更准确，识别率更高。

[1] ROY AD IT I,SURA L SHAM IK,M UKHERJEE JAYANTA. Gait recognition using pose kinem atics and pose energy im age[J].Signal Processing,2012,92:780-792.

[2] HUANG YI,XU DONG,CHAM TATJEN.Face an d human gait recognition using im age-to-class distance[J].IEEE Transactions on Circuits and System s for Video Techno logy,2010,20(3):431-438.

[3] SRUTI DAS CHOUDHURY,TARD I TJAH JAD I.Silhouette-based gait recognition using p rocrustes shape analysis and ellip tic Fourier descrip tors[J].Pattern Recognition,2012,45:3414-3426.

[4] 王科俊,刘丽丽,贲晛烨,等.基于步态能量图像和2维主成分分析的步态识别方法[J].中国图像图形学报,2009,14(12):2503-2509.

[5] ZHANG ERHU,ZHAO YONGWEI,XIONG WEI. Active energy im age p lus 2DLPP for gait recognition[J]. Signal Processing,2010,90:2295-2302.

[6] AVERBUCH AM IR,SEDELNIKOV ILYA,SHKOLNISKY YOEL.CT reconstruction from parallel and Fan-Beam p ro jections by 2-D d iscrete Radon transform[J].IEEE Transactions on Processing,2012,21(2):733-741.

[7] 贲晛烨.基于人体运动分析的步态识别算法研究[D].哈尔滨:哈尔滨工程大学,2010.

[8] 王科俊,贲晛烨,刘丽丽.采用Radon变换和二维主成分分析的步态识别算法[J].智能系统学报,2010,5(3):266-271.