日本“311”海啸对江苏北部沿海影响分析

袁春光，王义刚，黄惠明，蔡 辉，陈 橙

(河海大学海岸灾害及防护教育部重点实验室，江苏南京 210098)

海啸是指由海底地震、火山爆发和海底滑坡、塌陷所产生的具有超大波长和周期的大洋行波，当其接近近岸浅水区时，波速变小，波幅陡涨，有时可达30米以上，突然形成“水墙”，瞬时侵入滨海陆地，冲毁或卷去沿海建筑和人畜［1-2］。其中，海中地震引发的地壳垂向错动(“倾滑型”)可造成大面积水体突然升降，从而形成一系列波长数十到数百公里，周期为2～200 min的长重力波，一般称之为地震海啸。

地震海啸通常分为两种:一种是横越大洋或从远洋传播来的海啸，成为远洋海啸。例如，1960年智利发生8.7级特大地震海啸，在智利沿岸波高达20.4 m，海啸传到夏威夷时，波高尚超过11.0 m，在日本沿岸波高仍有6.1 m。另一种是近海海啸，海啸生成源地与其造成危害同处一地，所以海啸到达沿岸时间很短，有时只有几分钟或者几十分钟，危害巨大。例如，1983年的印尼6.5级地震引起的海啸，遇难人数为3.6万，克拉客托岛三分之一沉入海底。

北京时间2011年3月11日13时46分，位于日本宫城县以东太平洋海域(37.7°N，143.0°E)发成里氏9.0级地震(如图1)［3］，震源深度为24.4 km，14 133人遇难，13 346人失踪，超过10万人撤离。在地震发生后的20多个小时里，海啸波先后到达俄罗斯、中国、菲律宾、美国夏威夷和西海岸智利以及南美其他一些国家和地区沿海，各地均监测到了明显的海啸波。其中，美国及南美的智利等国家监测到的最大海啸波幅达到150～200 cm。地震发生后约4小时海啸波到达我国台湾东部沿海，随后波及我国大陆东南沿海，有关部门预计次日凌晨2点到达上海和江苏南通。台湾、福建、浙江、广东、江苏、上海、海南等省市监测到的海啸波波幅在3～55 cm之间，其中浙江沈家门和石浦海洋站分别监测到55 cm和52 cm的海啸波(如图2、3)［4］。受其影响，国家海洋预报台针对台湾地区和浙江沿岸发布2期海啸蓝色警报，这是我国开展海啸预警业务以来首次发布海啸警报。

图1 日本地震位置Fig.1 Japan earthquake location

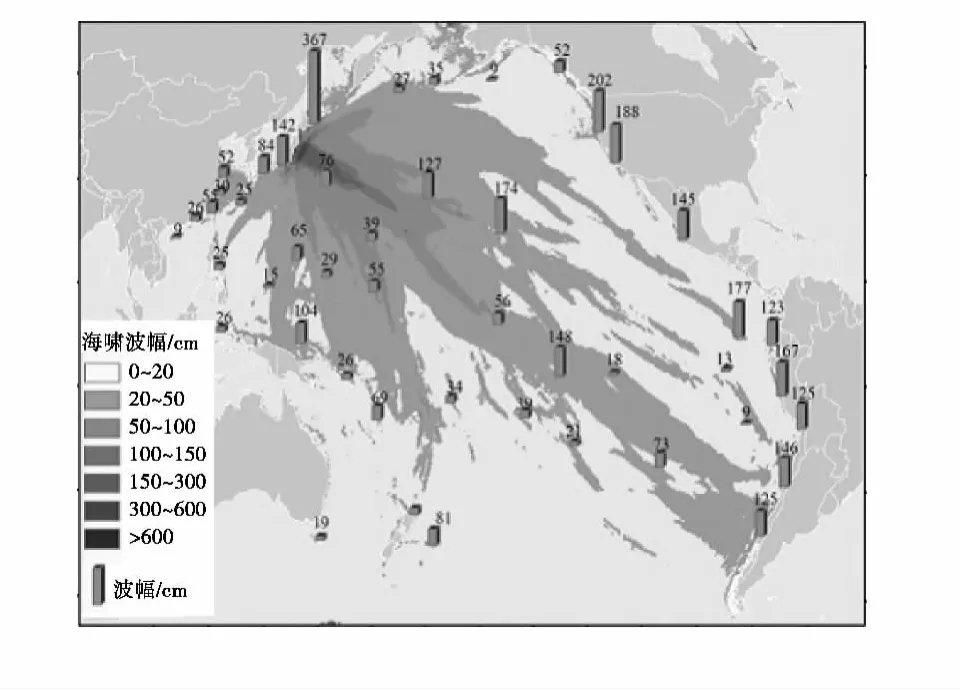
图2 2011年3月11日日本地震海啸及最大海啸波幅图［4］Fig.2 Japan tsunami maximum amplitude distribution on March 11，2011

1 数据来源和处理方法

将在对江苏灌河口处(站点位置如图4)海啸期间逐分钟潮位资料的分析的基础上，讨论“311”日本海啸对该地区的影响，并且讨论造成这种现象的原因。

波高和周期是刻画潮位波动的最基本的两个特征量。当海啸波趋向近岸浅水时波形发生变化，具体表现为波长变小，波高增加。实际上，海啸波高在近岸很大程度上取决于海底地形、坡度和海岸线的形状与走向。喇叭口或漏斗型的海岸地形有利于波能折射聚集，海啸将大幅提高。

卫星遥感、海上浮标和沿海潮位站是获得海啸增水数据的主要来源。由于受到各种天气和人为等因素的影响，从潮位信号中精确地提取海啸波仍然是比较困难的，介绍这方面文章也不多见。于福江认为［5］，海啸影响期间，潮位序列主要表现为较高频率的海啸波叠加在长周期的潮汐信号上，为了消除高频噪音，对潮位信号进行截断周期为10～136.53 min的带通滤波，并且认为经过以上处理方法得到的波动序列就是“干净”的海啸波动序列，序列中最大波高即认为是海啸引起的最大增水，以第一个到达潮位站的显著波峰或者波谷为准作为该站位的海啸到达时间。董非非［6］认为，把原始数据通过滤波器，滤掉气象潮、海洋背景噪音等的影响，得到的潮差(包含潮汐，也可能包含海啸信息)，扣除潮汐的影响，对最终得到的数据进行分析处理，可从周期(100～1 000 s)、波长等参数判断识别其是否含有海啸信息。

以上分离海啸波的方法主要问题在于如何确定滤波截断周期的上限和下限。海啸波周期范围一般在2～200 min之内，但是海啸波的波动并不会均匀分布在如此漫长的周期范围中，通常只会聚集在一个相对较窄的周期范围中。如果滤波的截断周期范围小于这个周期范围，则不能分离出全部的海啸波;如果截断周期范围大于这个周期范围，那么滤波结果中将掺杂不属于海啸波波动的“噪声”，从而造成结果不准确。以往对于海啸滤波周期范围的选取，主要依据个人经验，不同学者之间取值的差异很大，过滤出的海啸波也大小不同，这将影响后续的研究工作。

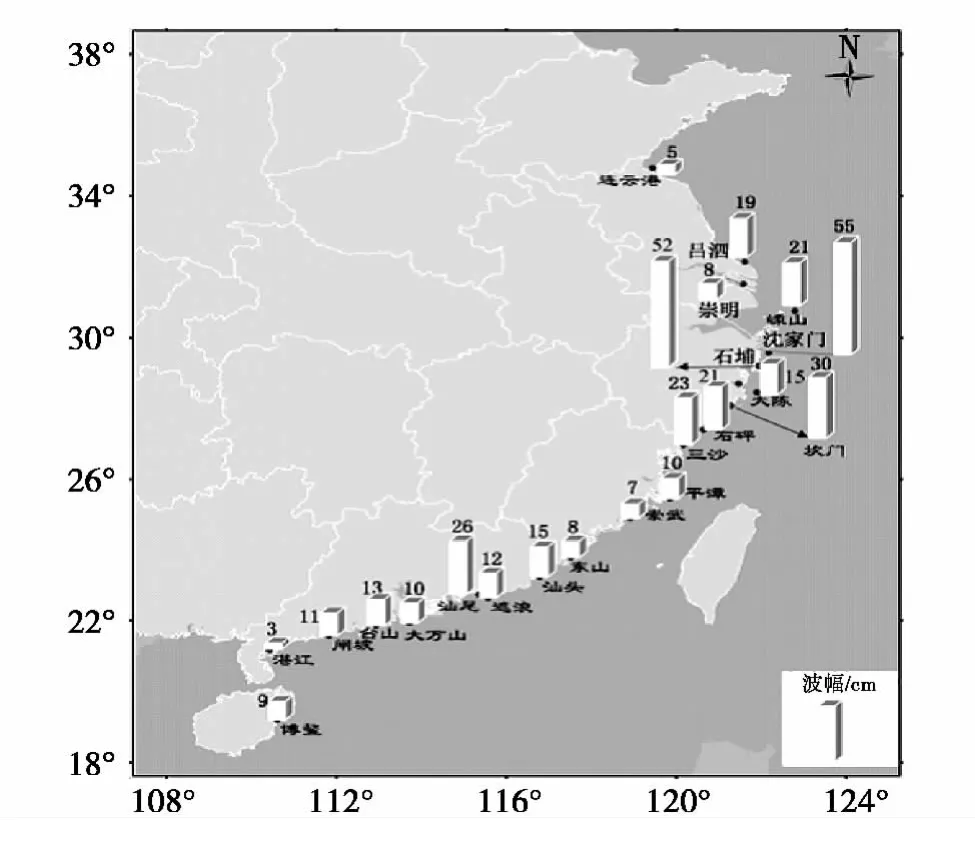
图3 2011年3月11日日本地震海啸中我国沿海潮位站最大海啸波幅［4］Fig.3 Maximum tsunami amplitude in tidal stations of China，March 11，2011

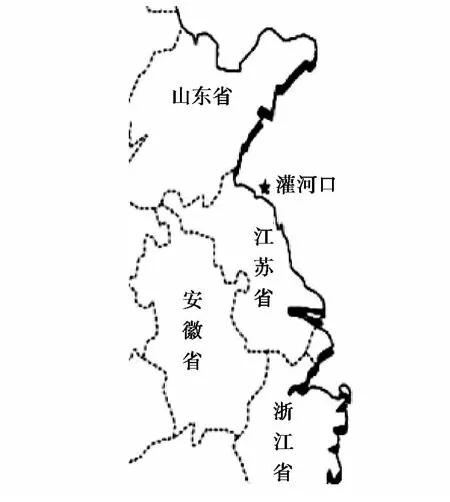
图4 灌河口测站位置示意Fig.4 Guanhekou station location

文中将多种信号分析的方法综合使用于潮位信号的分析中，形成一种新的综合分析海啸波的模式，更加准确全面地了解海啸波的各项物理特征。具体步骤如下:

首先，通过对同一潮位站过往一年369天的资料进行潮汐调和分析，预报出该潮位站海啸发生时间段的天文潮位，在不考虑海啸波与天文潮耦合的情况下，用海啸期间实测潮位减去预报潮位，这个差值即认为是由海啸和其他天气条件共同引起的增水。这一步主要是为了去除潮位资料中的长周期天文潮波。

其次，对这个差值序列信号以Morlet小波为小波母函数，应用连续小波分析方法，进行小波能量谱分析［7］。小波变换可以在波动序列的任意时刻对信号成分进行局部化分析，提取差值序列在时域和频率域上的局部性特征。小波能量谱分析是基于小波变换理论基础建立的，具有同时在时间域和频率域内识别振动强度的功能，并且可以聚焦到信号细节的分析。通过这种方法可以找出潮位信号中和海啸波动周期范围相似，持续时间相当，比较可疑的异常强烈波动。由于海啸发生的概率很低，海啸引起的水位波动只是偶尔发生，所以通过小波能量谱分析找出的异常波动必须具备严格的罕见性才有可能是海啸波。同时还应该根据潮位站位置与海啸发生位置之间的距离以及浅水波的传播速度，初步估算海啸波动到达潮位站的时间，并与可疑波动发生时刻进行对比。如果估算海啸波到达时间与可疑波动发生时间相近，则大大增加了可疑波动就是海啸波的可能;相反，如果估算海啸波到达时间与可疑波动发生时间相距甚远，那么可疑波动很可能是由于其他因素导致。

再次，将满足以上条件的可疑波动找出，确定周期范围之后，利用2阶或者更高阶数的Butter带通滤波器对差值序列在该周期范围内进行滤波。Butter滤波器的特点是通带处幅值特性平坦，可以通过提高阶数的方法提高逼近精度，但是同时也增大了计算量。这样滤出的波动即认为是海啸波，序列中最大波高即认为是海啸引起的最大增水。

最后，通过对滤波序列进行功率谱分析，进一步得出各种周期的波动对整体波动能量的贡献，从而更精确和全面的了解各种波动成分的运动特点。文中选用的功率谱分析方法是，先将过滤出的海啸波序列由快速Fourier变换获得能谱密度，再采用Welch算法［8］分成不重叠的6部分，然后取Fourier系数平均得到比较光滑的谱线。

采用以上海啸分离方法的优点是:1)能够比较针对性的对海啸波进行分离过滤，尤其是对受海啸作用影响不明显的潮位站，这种方法更加精确可行;2)采用多种方法相结合的方式对海啸波进行分析，可以从多个角度更加全面的了解海啸波波动的物理特性。

对于灌河口潮位站，海啸期间实测潮位摘取时间范围为2011年3月11日13时46分至3月14日0时，采样频率为1 min。用当地2009年8月至2010年8月369天的潮位资料进行潮汐调和分析，预报出海啸摘取期间该地区天文潮，如图5。将实测潮位值减去天文潮预报值，差值表示海啸或者其他天气因素引起的增水，如图6。从图中可以看出预报结果与实测值的误差大部分在20 cm以下，且波动相位吻合良好。

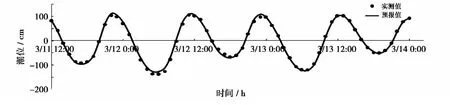
图5 灌河口海啸期间天文潮预报与实测潮位值的比较Fig.5 Comparison of astronomical and measured tide in Guanhekou during tsunami period

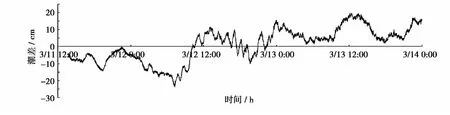
图6 海啸期间灌河口实测与预报的差值Fig.6 Difference between measured and predicted tide in Guanhekou during tsunami period

2 数据处理结果分析

通过小波能量谱图(如图7)可以发现，在整个3月份的图谱中，仅在3月11日8时之后有一股周期范围大致为25～100 min之间，波动能量比较强烈并且持续时间相对较长的波动进入灌河口站，而且在其余将近一个月的时间内，基本上没有周期在2～200 min范围内同等连续并且剧烈的波动，这与日本地震海啸发生的时间比较吻合，同时也在海啸波的周期范围之内。于是摘取3月11日13时46分至3月14日0时这一时段潮位进行进一步分析。分析表明，有一列周期范围在37～98.5 min的水位波动从3月12日早上6时26分左右开始影响灌河口站，并于3月13日凌晨2时26分左右结束，该周期范围恰好在海啸波的波动周期范围之内，也是初步怀疑的“可疑波动”。同时，对全年其他月份的潮位资料进行相同的分析，没有发现频率在海啸波周期范围之内，能量和持续时间和“疑似海啸波”同等量级的波动，这就愈发增大了这列波是海啸波的可能。

从时空角度上分析，位于江苏北部的灌河口站与日本地震震源之间的直线距离约为2 131 km，海啸长波的传播速度为，假设平均水深为120 m，由计算可得海啸波大约在地震发生之后1 035 min(3月12日7时1分)抵达灌河口，这与上文分析得到的开始影响时间比较一致。因此，可以基本确定图7中的波动就是由于日本地震引起，传播到灌河口潮位站的海啸波。

以带通周期为37～98.5 min对潮位信号进行滤波，如图8所示，横坐标是从海啸发生后开始计算的时间，单位为分钟。从图中可以看出，海啸波最大波高为5.05 cm，这与国家海洋局《2011年中国海洋灾害公报》中连云港潮位站监测到的海啸波高5 cm十分吻合(连云港至灌河口距离仅40 km左右)。同时，分别用2阶Butter带通滤波器和5阶Butter带通滤波器对潮位信号进行滤波，两者结果几乎没有差异，说明应用2阶Butter滤波器可以满足精度要求。用于福江的海啸滤波方法对潮位进行滤波，与文中方法滤波的波形进行对比发现，两列波动总体趋势很接近，都是先增大后减小。但是于福江方法的滤波中明显掺杂了噪声，波形参差不齐，而且最大波高为6.05 cm，比这里滤波的最大波高增大了20%，可见文中使用的过滤海啸波方法更加精确。进一步对滤波序列进行功率谱分析(如图9)可以看出，海啸波波能主要分布在周期为56～83 min的波动中，最大峰值出现在69.4 min，即对应海啸主周期。

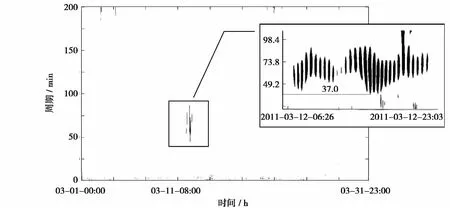
图7 小波能量谱分析Fig.7 Wavelet power spectrum

图8 海啸滤波Fig.8 Tsunami filter

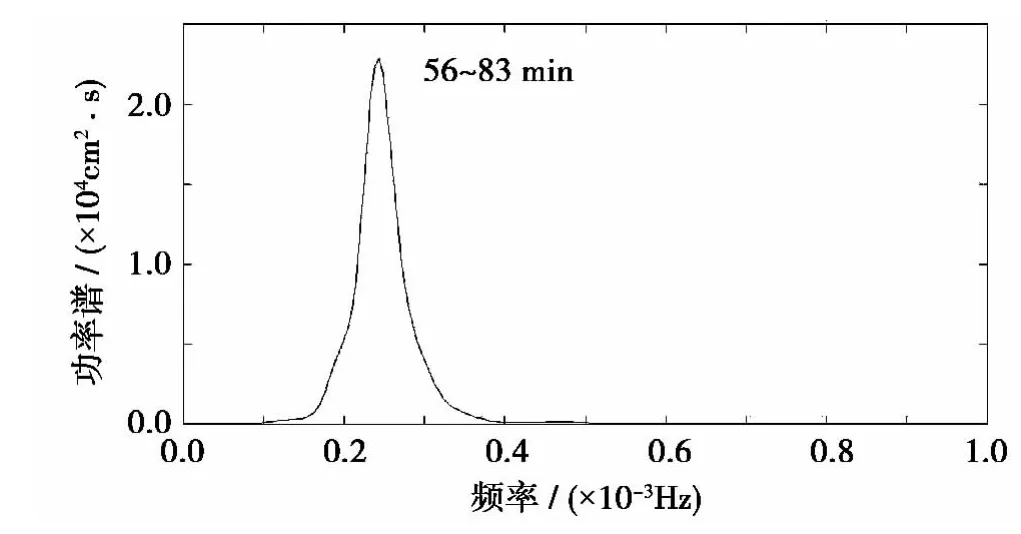
图9 海啸波功率谱Fig.9 Tsunami power spectrum

3 结果讨论

一般地震海啸波的最大波峰大多出现在第一次波动，但是对比图8，灌河口海啸波的最大波峰出现在海啸持续时间的中部，而且波高恰好为前半段平均波高的2倍左右。为了分析这种现象，采用美国Cornell大学基于长波方程浅水理论编译的COMCOT海啸模型［9］，进行简化的海啸传播数值模拟。基础地理信息数据采用NGDC的ETOPO1海底地形资料，模拟范围为118°～150°E ，20°～45°N，球面坐标系网格采取5 min的正方形网格。同时引用GCMT震源机制解作为震源参数，具体地震参数如表1［3］。应用Okada理论［10］模型进行海啸初始场计算，模拟时间为36 h。

海啸波数值模拟传播结果见图10。

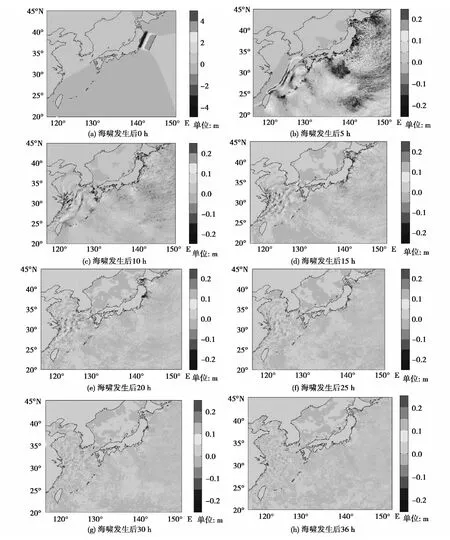
图10 海啸发生后不同时刻的海啸波模拟结果Fig.10 Tsunami wave simulation results after breaking out

表1 海啸地震参数表Tab.1 Tsunami seismic parameter

从图10可以看出，在模拟的海啸波向东海大陆架传播的过程中，海啸波一方面向长江口及南方的浙江福建沿岸逼近;另一方面也会向北方的黄海和渤海传播。向北方黄海传播的海啸波会先抵达山东半岛，然后分裂成两部分，一部分继续北上，向渤海挺近;另一部分则受到山东半岛阻挡反射，在山东半岛南侧和江苏沿岸形成第一波海啸波动。由于中国沿海近似一个圆弧形状，向长江口传播的海啸波抵达长江口后分裂成两部分，一部分沿江苏沿岸北上;另一部分沿浙江沿岸南下。这样一来，从长江口继续北上的海啸波将叠加到江苏沿岸第一波海啸波之上，从而最大海啸波峰值出现在两股海啸波叠加的地方，却不出现在第一波。同时，由山东半岛和江苏沿岸组成的“喇叭口型”的海岸地形也有利于海啸波在此叠加。如图11，与实测资料对比发现，海啸波数值模拟比实测数据有所提前，而且波形也有所不同。引起这些误差可能的原因:1)地形资料精度有限，不能完全符合实际情况，尤其在近岸，这个问题十分突出。2)受水深和岸滩资料不够准确影响，网格尺寸比较粗大，只能选择距离灌河口测站比较接近的网格节点水位值代表实际测站。3)实际的海域底部摩阻应该用一个曼宁系数场来表示，由于缺少资料这里只用常数0.013代表。对于冲绳海槽以东的太平洋海域，曼宁系数应该更小，而黄海海域应该更大一些。4)实际海底地震引发的水位波动比较复杂，这里用Okada方法进行简化只是一种近似。同时，海底地震参数的测量也存在技术障碍，不同研究机构给出的地震参数各有不同，也直接影响海啸模拟的精度。其中原因1)和2)主要影响海啸波传播速度;3)则直接影响海啸在传播中的波高变化。虽然以上数值模拟存在精度问题，仍然可以明显看出海啸波动先逐渐增大，然后逐渐减小的规律，这也证明了海啸波动在这里发生了叠加。

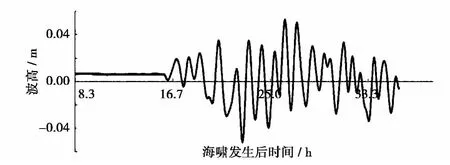
图11 灌河口处海啸波高数值模拟结果Fig.11 Numerical simulation of tsunami wave in Guanhekou

依据以上观点，实际海啸首波引起灌河口站的波动低于5.05 cm，大约只有2.5 cm左右，5.05 cm是后期由于岸线形状引起波动叠加之后的结果。

4 结语

1)通过对灌河口实测潮位资料的分析得出，2011年3月11日发生在日本的地震海啸于3月12日早上06∶26左右开始影响该站，3月13日凌晨02∶26左右结束影响。海啸波周期范围为37～98.5 min，最大波高为5.05 cm，主周期为69.4 min左右。

2)与其它从潮位中过滤海啸波的方法对比分析，这里使用的滤波方法更加精确，并且更加全面、直观地表现出海啸波波动的各项物理特性。

3)利用简化的海啸波数值模型从一定程度上模拟了海啸波在中国沿海的传播。模拟结果分析得出，由太平洋经过冲绳海槽向中国沿海传播的海啸波会一方面向东南沿海逼近，另一方面也向黄海海域挺进。由于地形的影响，海啸波产生了反射，这样最大波峰将出现在两股波叠加后的时刻。这就是灌河口站滤出的海啸波最大波峰不在第一波的主要原因。

4)由数值模拟可知，灌河口站由海啸直接引起的海啸波大约只有2.5 cm左右，但是海啸波叠加之后，最大波高为5.05 cm，是之前的2倍。虽然海啸波高量值不大，但是海啸预报中应该全面考虑地理位置特点，综合分析海啸波运动的反射叠加等特征，从而提高预报质量。

［1］ 于福江，叶 琳，王喜年.1994年发生在台湾海峡的一次地震海啸的数值模拟［J］.海洋学报，2001，6(23):30-39.

［2］ 叶 琳，于福江，吴 玮.我国海啸灾害及预警现状与建议［J］.海洋预报，2005，22(增刊):147-157.

［3］ 王培涛，于福江，赵联大，等.2011年3月11日日本地震海啸越洋传播及对中国影像的数值分析［J］.地球物理学报，2012，9(55):3088-3095.

［4］ 国家海洋局2011年海洋灾害公报［ED/OL］.http://www.soa.gov.cn/soa/index.html，2013-05-10-18:00.

［5］ 于福江，原 野，赵联大，等.2010年2月27日智利8.8级地震海啸对我国影响分析［J］.科学通报，2010，55(1):1-8.

［6］ 董非非.海啸在东海大陆架传播的研究与识别［D］.兰州:中国地震局兰州地震研究所，2009.

［7］ 谢 利.小波变换及小波能量谱在多尺度分析中的应用［J］.中山大学研究生学刊:自然科学版，1998，19(增刊):101-102.

［8］ Welch P D.The use of fast Fourier transform for the estimation of power spectra-A method based on time averaging over short，modified periodograms［J］.IEEE Trans Audio Electroacoust，1967，AU-15:70-73.

［9］ 姚 远，蔡树群，王盛安.海啸波数值模拟的研究现状［J］.海洋科学进展，2007，25(4):487-494.

［10］ Okada Y.Surface deformation due to shear and tensile faults in a half-space［J］.Bulletin of the Seismological Society of America，1985，75:1135-1154.