偏心荷载作用下条形浅基础荷载-变形特性数值分析

罗 强，

(1.南阳师范学院土木建筑工程学院，河南南阳 473061;2.大连理工大学土木工程学院岩土工程研究所，辽宁大连 116024)

在许多实际岩土工程问题中，例如基坑开挖、浅基础地基承载力与变形特性、地震或波浪荷载对海床的作用［1-2］等，主应力方向的旋转所引起的初始主应力状态的改变是不容忽视的。在土体主应力方向的旋转过程中，主应力方向与塑性主应变增量方向的旋转变化趋势并不是一致的，即存在非共轴现象，该现象在许多室内实验中已被观测到［3-5］。合理描述非共轴现象的理论是当前土力学研究中的热点问题之一，这些非共轴理论包括:双剪理论［6-7］、塑性势双剪理论［8］、亚塑性理论［9］以及屈服角点结构理论［10］。国内外研究学者针对非共轴理论及其应用进行了系统的研究［11-13］。

当地基承受浅基础所传递的上部荷载作用时，浅基础边缘下方土体将会产生显著的剪切变形，从而引起主应力方向的旋转。在主应力方向旋转过程中会产生非共轴现象，因此采用有限元方法分析浅基础荷载-变形问题时应当考虑非共轴现象的影响。Yu等［14-15］将角点结构非共轴模型应用到浅基础荷载-变形问题的有限元计算中，他们认为非共轴模型计算得到的基础沉降要比共轴模型的结果大很多。Yang Y和Yu H S［16］采用非共轴本构模型对浅基础荷载-变形问题进行有限元数值分析，研究了非共轴现象对基础沉降和地基承载力的影响。上述研究工作主要在中心加载情况下研究了非共轴现象对地基荷载-变形特性的影响，然而，现实中存在大量的偏心荷载作用情况;在偏心荷载情况下进行数值计算容易产生数值计算不收敛问题，因此，有必要在偏心荷载作用情况下研究非共轴现象对浅基础荷载-变形特性的影响。

基于屈服角点结构非共轴理论，建立了一种非共轴本构模型，通过有限元软件ABAQUS的二次开发子程序UMAT，将该模型运用到有限元数值计算中。首先，在理想的荷载、位移边界条件下对中密砂单剪试验进行数值模拟，研究了非共轴现象及其对应力-应变关系的影响，将数值计算结果与Roscoe的试验结果［4］进行对比。然后，针对偏心荷载作用下条形浅基础荷载-变形特性进行数值分析，研究了非共轴现象对荷载-位移关系的影响，以及土体单元在主应力方向旋转过程中的非共轴现象。

1 非共轴本构模型

屈服角点结构非共轴理论［10］是以Drucker-Prager弹塑性理论的圆形屈服面为基础，增加一个与屈服面相切的非共轴塑性应变增量，它与共轴塑性应变增量在是相正交的，如图1所示。

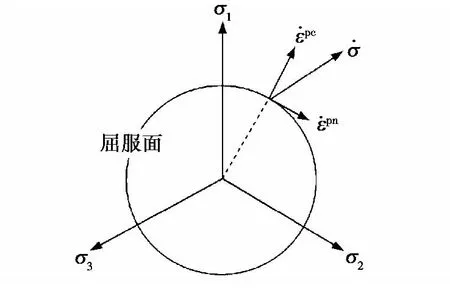
图1 非共轴、共轴塑性应变增量在屈服面上的关系Fig.1 Schematic illustration of non-coaxial and coaxial plastic strain rates

根据屈服角点结构非共轴理论，塑性应变增量ε·ij可以表达为

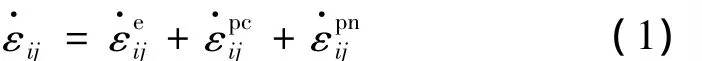
其中，等号右边的三项分别为弹性应变增量、共轴塑性应变增量和非共轴塑性应变增量。

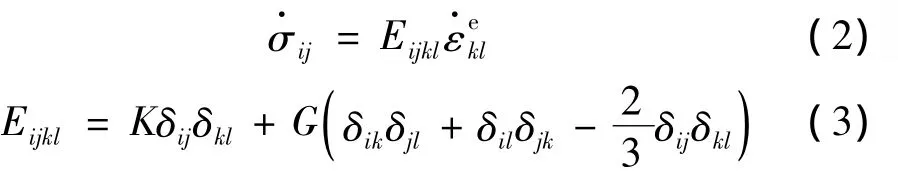
式中:K，G为土体材料的体积模量和剪切模量;δij为Kronecker函数。

采用相关联的流动法则，屈服函数(f)与塑性势函数(g)采用相同的表达形式:

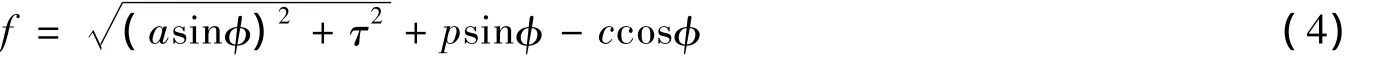
其中，c为黏聚力。当参数a=0.5ccotφ时，式(4)与传统Drucker-Prager屈服函数相一致。

在理想弹塑性情况下，式(4)中的φ为峰值内摩擦角。在应变硬化情况下，φ为机动内摩擦角，其为累积塑性偏应变γpc的函数［17］，如下所示:

其中，φult为材料的峰值内摩擦角，由常规三轴排水剪切试验得到;参数a1=-11.105［17］;参数a2=0.4。

其中，Kp为塑性硬化模量。

其中，H采用式(5)的表达形式，Ha=γpc。

非共轴塑性模量hnc假定为累积塑性应变ξp的函数［16］:

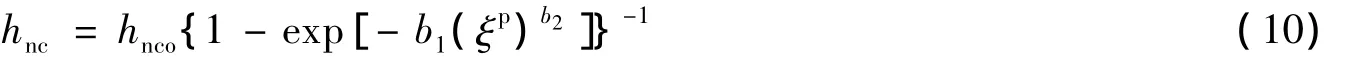
式中:hnco为初始非共轴塑性模量，b1和b2为模型系数，其数值分别为-16和0.7。

将式(2)、(6)、(9)代入式(1)中，可得到非共轴弹塑性本构模型的表达形式:

其中，Rij= ∂g/∂σij，lij= ∂f/∂σij，为非共轴模型的弹塑性刚度矩阵。

通过有限元程序ABAQUS里面的用户材料子程序UMAT，采用显式积分算法和自动分步相结合的方法［18］，对共轴和非共轴模型进行数值积分。

2 单剪试验数值模拟及结果分析

有限元模型采用四边形平面应变单元，其类型为八节点二次缩减积分单元。在模型顶边施加水平位移边界条件，模型的左右两边保持直线状态。模型底边的竖向和水平方向位移均被固定，竖向压力σyy施加在模型的顶面。由于剪应力τxy的作用，模型沿水平方向将会产生应力变化Δσxx、竖直方向的应变εyy以及主应力方向的旋转。主应力方向和塑性主应变增量方向的旋转如图2所示，虚线为变形后的状态，实线为初始状态;α为主应力或塑性主应变增量方向的旋转角度。

采用相对密度Dr=40%的中密砂，其内摩擦角峰值φult=36°。在理想弹塑性和应变硬化情况下，剪切模量G分别取为150 MPa和30 MPa。静止侧压力系数Ko取为0.2和0.5。竖向应力取为135 kPa。非共轴模型中的hnco/G分别取0.2、0.4和0.8。

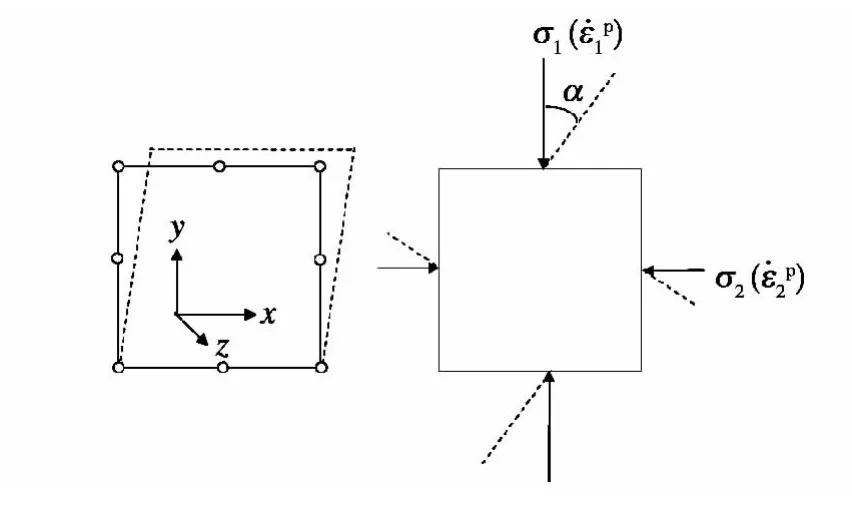
图2 主应力方向和塑性主应变增量方向的旋转Fig.2 Rotation of directions of principal stress and principal plastic strain rate

2.1 剪应力比-剪应变关系

在理想弹塑性和应变硬化情况下，计算得到的剪应力比(τxy/σyy)-剪应变(γxy)关系如图3所示。

由图3可知:1)非共轴模型计算结果的增长速度滞后于共轴模型计算结果的增长速度，即非共轴现象对应力-应变关系曲线具有“软化”作用。当剪应力比达到极值时，两种模型的计算结果之间的差异将消失。2)随着hnco/G的增加，非共轴现象的影响逐渐减小，两种模型计算结果之间的差异逐渐减小。3)与理想弹塑性计算结果相比，两种模型计算结果之间的差异在应变硬化情况下更加显著。

2.2 主应力方向和塑性主应变增量方向的旋转

对主应力方向和塑性主应变增量方向的旋转规律进行分析，从而对非共轴现象进行研究。以Ko=0.2时的计算结果为例，如图4所示。

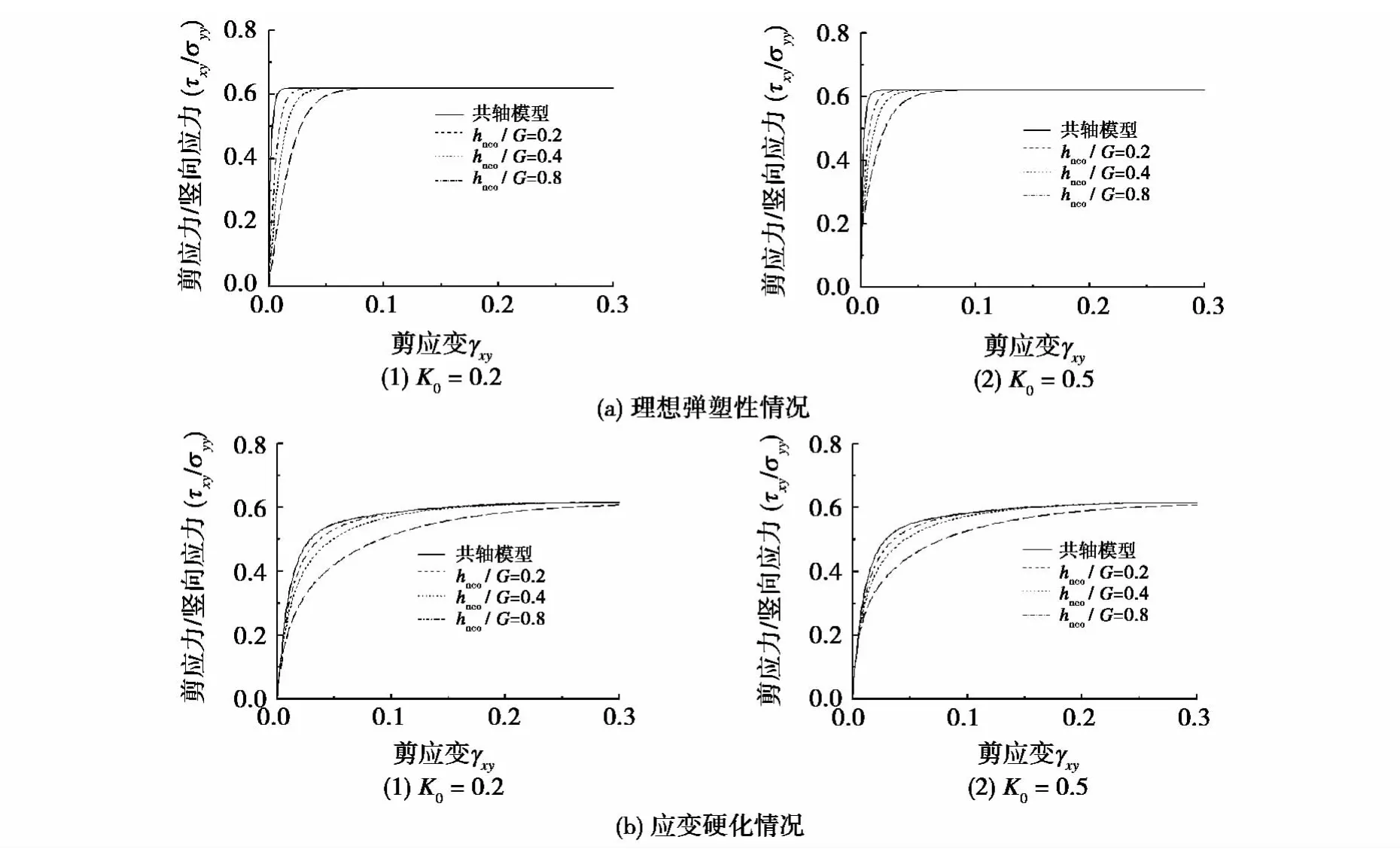
图3 剪应力比-剪应变关系Fig.3 Curves of shear stress ratio-shear strain

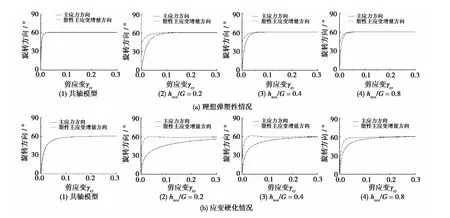
图4 主应力和塑性主应变增量方向的旋转Fig.4 Predictions of the orientations of major principal stress and plastic strain rate

由图4可知:1)非共轴模型得到的主应力方向和塑性主应变增量方向在剪切变形的初期是不重合的，主应力方向的增长趋势滞后于塑性主应变增量方向的增长趋势;随着剪切变形的发展，两者逐渐趋于一致。2)随着hnco/G的增长，主应力方向与塑性主应变增量方向之间的差异逐渐减小，非共轴现象逐渐减弱。3)与理想弹塑性计算结果相比，非共轴现象在应变硬化情况下更加明显。

2.3 数值计算与单剪试验的结果对比分析

在Roscoe的中密砂单剪试验过程中［4］，作用于试样的竖向应力为135 kPa，试验结果如图5所示。

将图3(b)和图4(b)的数值计算结果与图5的试验结果进行对比，可以发现:非共轴模型能够合理地反映非共轴现象;试验结果与非共轴模型的计算结果比较接近。

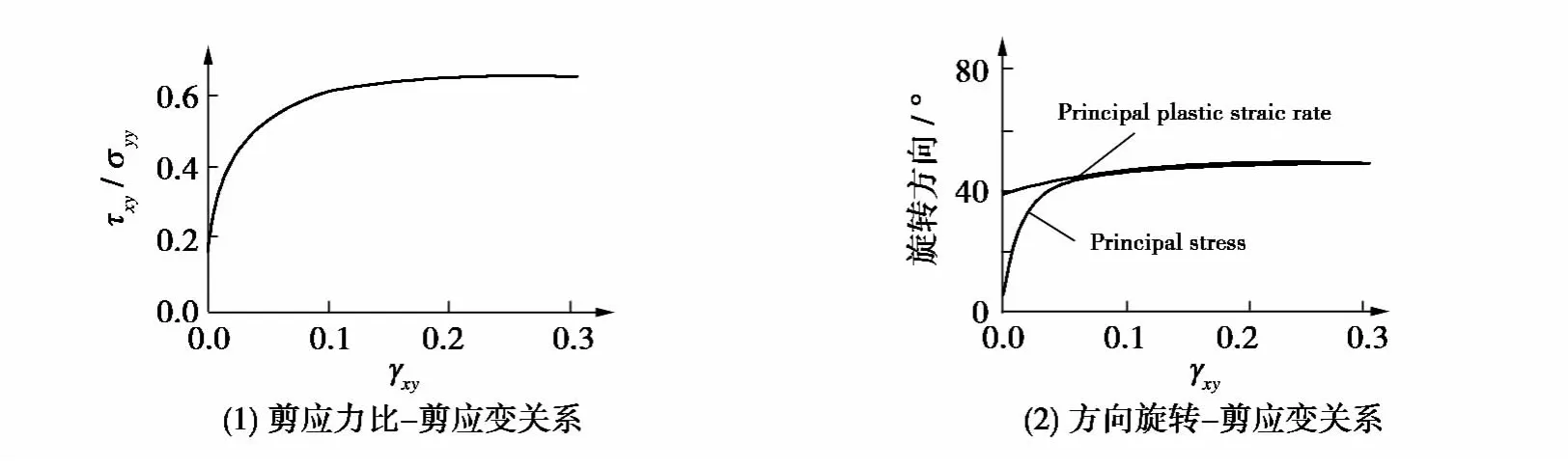
图5 单剪试验结果Fig.5 Results of simple shear test

3 偏心荷载作用下浅基础荷载-变形特性的数值分析

针对宽度D=1 m的条形浅基础，采用平面应变单元建立有限元模型:约束模型侧边的水平位移，约束模型底边的竖向位移和水平位移;地基表面施加均布竖向荷载q=100 kPa。为了模拟偏心加载，在距离浅基础中心处不同水平距离的位置(e=D/8，e=2D/8，e=4D/8，e为偏心距)施加竖向位移。

地基材料的数值计算参数:Dr=40%，φult=36°，Ko=0.5，干密度ρd=1.473 g/cm3，泊松比ν=0.3。在理想弹塑性和应变硬化情况下，剪切模量G分别取为150 MPa和30 MPa。浅基础采用线弹性本构模型，E=2.1×105MPa，ν=0.125。非共轴模型中的hnco/G分别取0.3、0.4和1.0。

3.1 荷载-位移关系

在理想弹塑性和应变硬化情况下，数值计算得到的荷载-位移关系如图6和7所示。竖向、水平荷载为浅基础下方第一层土体单元的竖向、水平应力的平均值，水平坐标为归一化竖向位移(V/D)。

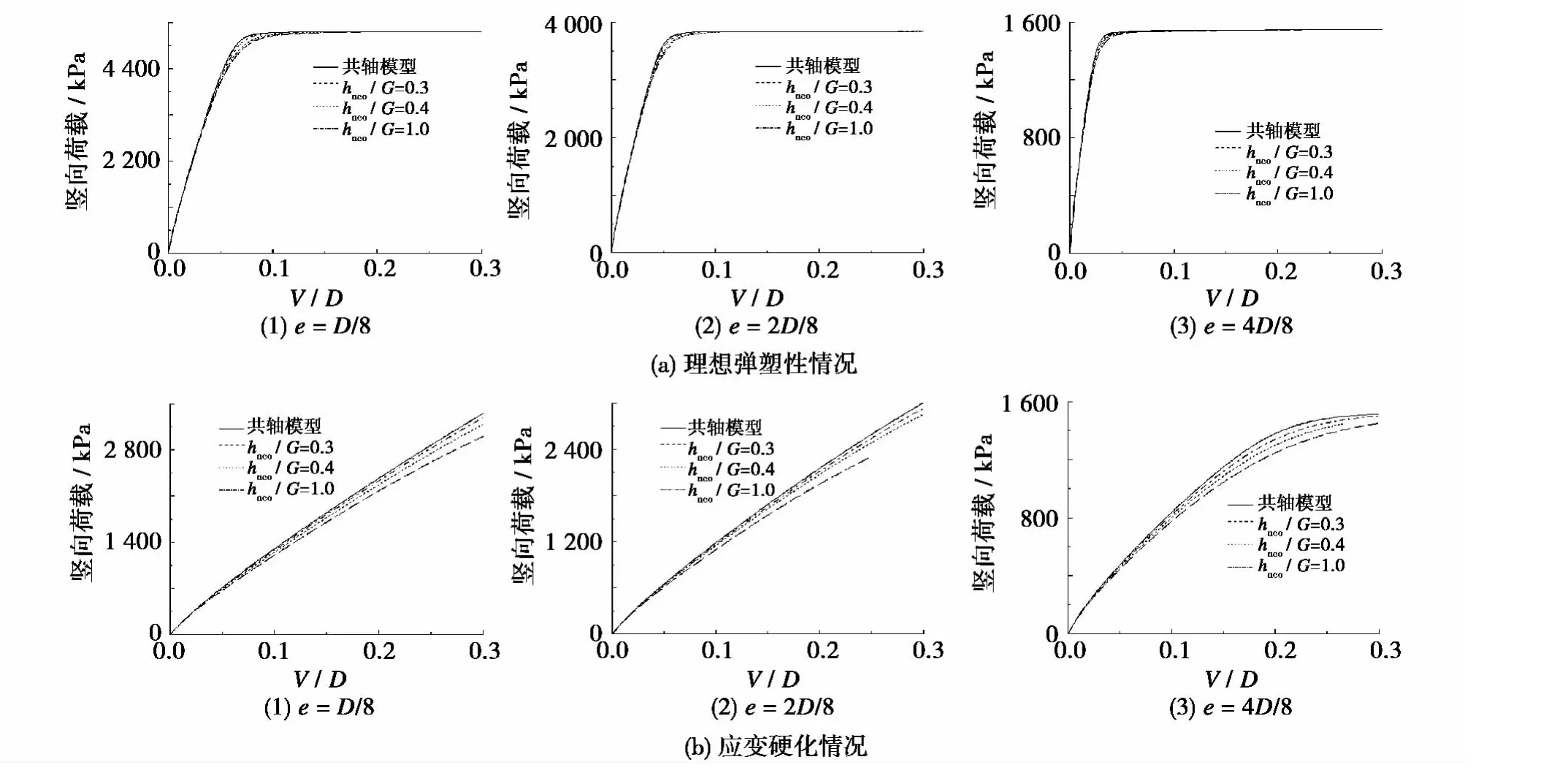
图6 地基竖向荷载-位移关系Fig.6 Curves of vertical load-settlement

由图6和7可知:1)在理想弹塑性情况下分析竖向荷载时(如图6(a)所示)，非共轴模型所得到的竖向荷载达到极值的增长速度滞后于共轴模型的结果。当竖向荷载达到极值时，共轴与非共轴模型计算结果之间的差异将消失。2)在理想弹塑性情况下分析水平荷载时(如图7(a)所示)，水平荷载随着基础沉降的增加而增长至极值，非共轴模型所得到的水平荷载的增长速度滞后于共轴模型的结果，非共轴模型所得到的极值要低于共轴模型的结果。然后，水平荷载由极值逐渐减小至最小值，非共轴模型的计算结果的减小速度要滞后于共轴模型计算结果。当水平荷载减小到最小值时，非共轴与共轴模型计算结果之间的差异消失。3)在应变硬化情况下，竖向和水平荷载均没有达到极值，非共轴模型计算结果的增长速度滞后于共轴模型的结果。与理想弹塑性情况下的计算结果相比，非共轴模型与共轴模型计算结果之间的差异在应变硬化情况下更加明显。4)随着hnco/G的减小，非共轴与共轴模型计算结果之间的差异越来越大。

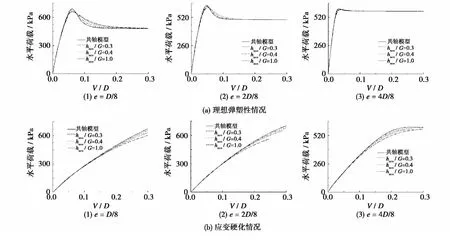
图7 地基水平荷载-位移关系Fig.7 Curves of horizontal load-settlement

3.2 主应力方向和塑性主应变增量方向的旋转

根据非共轴模型的计算结果(hnco/G=0.3)，针对浅基础右侧边缘下方土体单元(H=0.1D)，对主应力方向和塑性主应变增量方向的旋转规律进行研究，如图8所示。其中，H表示所选取土体单元距离地基表面的距离，D表示浅基础的宽度。

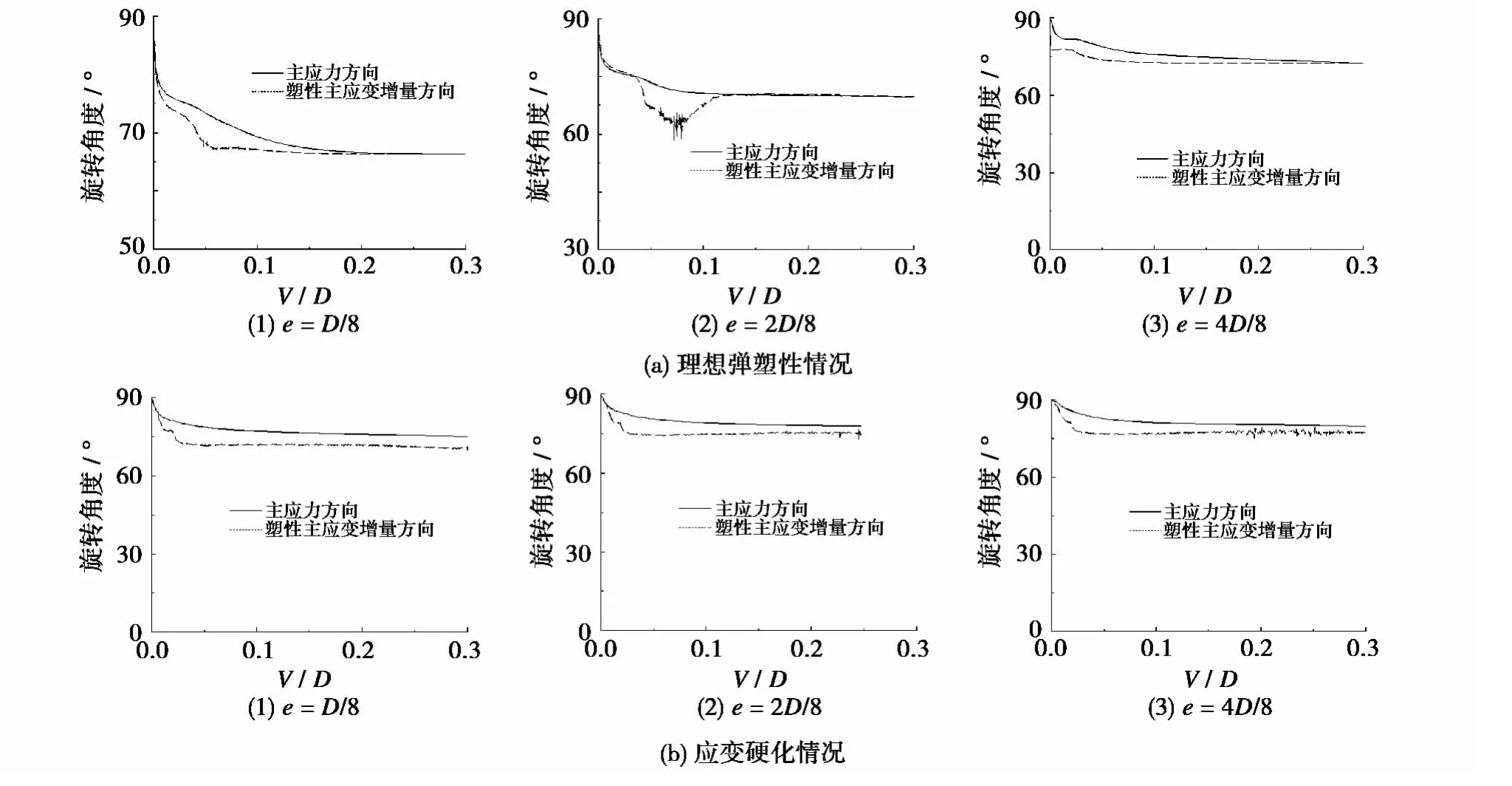
图8 主应力与塑性主应变增量方向的旋转Fig.8 Rotations of directions of major principal stress and plastic strain rate

由图8可知:1)在地基变形的初期，非共轴现象比较明显，主应力方向的减小速度要滞后于塑性主应变增量方向的速度;随着地基沉降的增加，非共轴现象逐渐减弱。2)在应变硬化情况下，非共轴现象在基础沉降较大时仍然比较明显。与理想弹塑性的计算结果相比，非共轴现象在应变硬化情况下更加明显。3)在应变硬化情况下，随着偏心距的增加，非共轴模型的数值收敛性能逐渐变差。

4 结语

针对偏心荷载作用下条形浅基础荷载-变形特性进行数值分析，研究了非共轴现象对荷载-位移关系的影响。研究结果表明:1)在地基变形的初期，非共轴现象比较明显，主应力方向的减小速度要滞后于塑性主应变增量方向的减小速度;随着地基沉降的增加，这种差异逐渐减小。2)在应变硬化情况下，竖向和水平荷载均没有达到极值，两种模型计算结果之间的差异随着基础沉降的增加而增加;非共轴现象在基础沉降较大时仍然比较明显。3)与理想弹塑性情况下的计算结果相比，非共轴模型与共轴模型计算结果之间的差异在应变硬化情况下更加明显。4)随着hnco/G的减小，非共轴与共轴模型计算结果之间的差异越来越明显。

［1］ Luan M T，Wang D.Dynamic response of seabed under wave-induced lodaing［C］//Proeeednigs of 4th International Conference on Recent Advances of Geotechnical Earthquake Engineering and soil Dynamics.2001:26-31.

［2］ 钱寿易，楼志刚，杜金声.海洋波浪作用下土动力特性的研究现状和发展［J］.岩土工程学报，1982，4(1):16-23.

［3］ Roscoe K H，Bassett R H，Cole E R.Principal axes observed during simple shear of a sand［C］//Proceedings of the Geotechnique.1967:231-237.

［4］ Roscoe K H.The influence of strains in soil mechanics［J］.Geotechnique，1970，20(2):129-170.

［5］ Oda M，Konishi J.Microscopic deformation mechanism of granular material in simple shear［J］.Soils and Foundations，1974，14(4):25-38.

［6］ Spencer A J M.A theory of the kinematics of ideal soils under plane strain conditions［J］.Journal of Mechanics and Physics of Solids，1964，12(5):337-351.

［7］ De Josselin De Jong G.The double-sliding，free-rotating model for granular assemblies［J］.Geotechnique，1971，21(2):155-163.

［8］ Harris D.Constitutive equations for planar deformations of rigid-plastic materials［J］.Journal of Mechanics and Physics of Solids，1993，41(9):1515-1531.

［9］ Kolymbas D.An outline of hypoplasticity［J］.Archive Applied Mechanics，1991，61:143-151.

［10］ Rudnicki J W，Rice J R.Conditions for the localisation of deformation in pressure-sensitive dilatant materials［J］.Journal of Mechanics and Physics of Solids，1975，23(6):371-394.

［11］扈 萍，黄茂松，钱建固，等.砂土非共轴特性的本构模拟［J］.岩土工程学报，2009，31(5):793-798.

［12］ Hashiguchi K，Tsutsumi S.Shear band formation analysis in soils by the subloading surface model with tangential stress rate effect［J］.International Journal of Plasticity，2003，19(10):1651-1677.

［13］ Yang Yunmin，Yu H S.Numerical simulations of simple shear with non-coaxial models［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2006，30(1):1-19.

［14］ Yu H S，Yuan X.The importance of accounting for non-coaxial behaviour in modelling soil-structure interaction［C］//Proceedings of the 11th International Conference of IACMAG.2005:709-718.

［15］ Yu H S，Yuan X.On a class of non-coaxial plasticity models for granular soils［C］//Proceedings of the Royal Society of London.2006:725-748.

［16］ Yunming Yang，Haisui Yu.Application of a non-coaxial soil model in shallow foundations［J］.Geomechanics and Geoengineering:An International Journal，2006，1(2):139-150.

［17］ Papamichos E，Vardoulakis I.Shear band formation in sand according to non-coaxial plasticity model［J］.Geotechnique，1995，45(5):649-661.

［18］罗 强，王忠涛，栾茂田，等.非共轴本构模型在地基承载力数值计算中若干影响因素的探讨［J］.岩土力学，2011，32(S1):732-737.