基于高阶滑模控制器的水下潜器运动控制

邓春楠，葛 彤，吴 超

(上海交通大学船舶海洋与建筑工程学院水下工程研究所，上海 200240)

水下潜器在深海石油勘测、海底科学研究等方面扮演着重要作用，随着海洋开发工作的日趋重要，水下潜器的性能要求也在不断地提高。

水下潜器的运动控制往往会遇到以下几个难题:

1)海底环境光线弱，水下照明能力弱，往往需要潜器具有一定的自动控制能力;

2)小型潜器能够携带的能源和传感器有限，往往无法准确获得水流速度等信息;

3)水下潜器模型呈现显著的非线性，并且水动力系数存在时变性，利用估算法或实验值所获得的水动力系数存在较大偏差。

近年来，许多不同的控制方法被应用到水下潜器的运动控制中。Wonchang L，et al［1］设计了一种基于模糊逻辑的控制器。Antonelli G［2］和Gristi R［3］等设计了自适应控制器用于解决水下潜器参数时变的现象。龙建军［4］等提出了一种基于功能原理的潜器模型参数辨识方法，并通过实验值验证了有效性。文献［5-6］中提出了一种模型无关控制器，并证明了在初始条件匹配的情况下，这种控制器可以达到很好的控制效果。

模糊逻辑控制的缺点是需要很多的专家经验，控制器参数过多，难于调节;基于模型的算法在无法获得精确模型参数时，往往难以得到很好的控制效果;基于功能原理的参数辨识方法需要待辨识模型有显著的能量传递关系，并不能辨识所有的水动力系数。鉴于此，设计了一种基于变滑动平面的模型无关高阶滑模控制器，并通过合理的过渡过程设计，使控制器可以适应于任意的初始条件。

1 潜器数学模型

以上海交通大学水下工程研究所研制的某型AUV为实际背景。此AUV共装备有4个推进器——艉部两个主推，一个侧向推进器，一个垂向推进器，共控制4个自由度，X、Y、Z方向和艏向。AUV关于垂直面对称，无控制横滚和纵倾的机构，无翼和舵。通过在不同位置配置重块，可以使AUV在运动过程中的横滚和纵倾保持在很小的量，建模时将纵倾角和横倾角设为0°，故需要建立4自由度模型。目前主要建模的方法有机理建模和模型水池实验建模。模型水池实验建模的成本很高，一般采用机理建模方法。

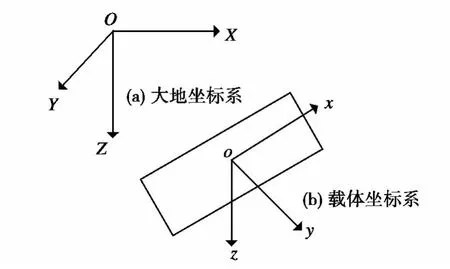
图1 参考坐标系定义Fig.1 Reference coordinate system

1.1 坐标系和参数定义

1)大地坐标系O-XYZ

大地坐标系 O-XYZ，原点为 O，OX、OY、OZ 三个轴分别沿北向、东向和垂向(向下)。忽略地球的自转，可以认为坐标系O-XYZ是一个惯性坐标系，牛顿运动定律在其中适用(见图1(a))。

2)载体坐标系o-xyz

载体坐标系o-xyz与载体固连，原点为o，轴oy指向潜器右舷，轴oz垂直于oy轴并指向下，轴ox垂直于轴oy和轴oz指向船艏，其方向使o-xyz构成右手坐标系(见图1(b))。

3)参数定义

模型中参数定义表1。

表1 参数定义Tab.1 Parameter definitions

1.2 潜器模型

水下潜器在水中做空间运动时，其所受到的力按照与运动状态的关系分为静力和动力两种:静力即运载器本身的重力和浮力;而动力是指运载器在水中运动时，水流体会在运载器表面参生反作用力，称为水动力，它是运载器表面水的正压力和切应力的积分，这里正压力指扣除了产生浮力的静压力后的动压力。

水动力取决于运载器本身的运动，反过来又影响运载器的运动，因此是运动状态的函数。水动力按照其产生原因可分为惯性力和粘性力两大类。惯性类水动力是指运载器在水中运动时，会强迫周围的水流体随运载器一起运动，相当于运载器的质量和转动惯量等的增加。这部分增加的质量和转动惯量等就称为惯性类水动力，是运动加速度的函数。而粘性类水动力是指运载器在水中运动时，会受到水流体的阻力和升力的作用，前者与来流方向一致，后者与来流方向垂直。阻力和升力在本质上是由于水的粘性造成的，因此成为粘性类水动力，是运动速度的函数［7］。

作为仿真中潜器主体模型，需要做如下假设:

1)流体无旋;

2)虽然为了稳定性考虑需要将重心设置在浮心之下，但他们之间的距离很小，可以近似的将重力和浮力产生的合力和合力矩都设为0，将这一部分的力作为干扰考虑;

3)水下潜器是刚体;

4)在考虑重心的加速度分量时忽略地球自转的影响;

5)作用在水下潜器的主要外力包括水动力、推进器力;

6)潜器工作在近海底，不考虑近水面波浪力;

7)潜器为低速潜器，故只考虑线性粘性阻力部分，并在建模过程中忽略高阶水动力耦合系数。

建立载体坐标系下潜器动力学模型［8］:

潜器运动学模型:

式中:［δ1，δ2，δ3，δ4］为模型中未建模的动态和未知干扰的总和，为未知量;m11=m-X˙u;m22=m-Y˙v;m33=m-Z˙w;m44=Izz-N˙r。方程(1)～(2)即为仿真中的潜器模型。

2 高阶滑模控制器设计

首先，设名义参考˙ηr［5-6］:

其中，α和Ki为对角正定矩阵，sgn(x)为符号函数，并且:

式中:k＞0;S(t0)代表S(t)的初值=η-ηd，η=［X，Y，Z，ψ］T，ηd为指令值。定义扩展误差变量:

将式(3)代入式(7)中，得:

模型(1)和(2)中的控制量:

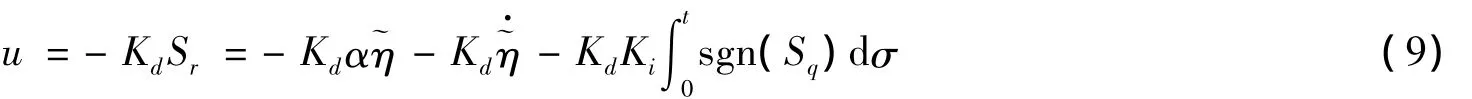
控制器的稳定性证明如下［9-11］:

对式(8)取微分:

取能量函数:

对上式取微分:

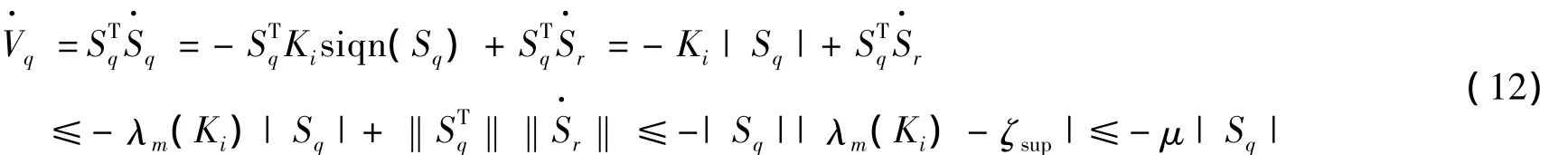
当滑动模态存在并且对于所有时间Sq(t)=0，可以得出如下结论:

即η→ηd，→。所以被控指令在有限时间内可以趋近于待跟踪值，控制器是稳定的。

3 过渡过程和变滑动模态设计

从上节可以看出，只有当Sq(t0)=0或很小时，滑动模态是在所有时间内存在的。而对于水下潜器这种系统来讲，很难在初始时刻满足匹配条件，为了使滑动模态在任意时刻总是存在的，可以借鉴变滑动模态的思想，设计一个时变的滑动模态［12-13］。

3.1 时间基准发生器(TBG)

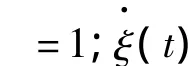
并且tb不依赖任何初始条件，当ξ(Tb)=1时，上式变为

这里选择ξ(t)的动态如下:

其中，r＞0，0＜β1＜1，0＜β2＜1。

当满足上述条件时，式(14)的解:

3.2 过渡过程的设置

高阶滑模控制器实质上是一个大增益控制器，在系统从初始状态到收敛(平衡点)的过程中，往往存在一定的震荡和超调，尤其在控制受限的前提下，高阶滑模控制器的输出不能保证系统在设计的有限时间内到达平衡点(小型潜器的输出受限很大，推力的最大值往往比较小)。实际上，由于实际系统都具有惯性，系统输出只能从初始状态开始缓慢变化，而控制目标的初始值却可能是一些比较大的量，容易给予系统很大的初始冲击，使系统的实际行为产生超调，因此，如果能够降低起始误差，那么在不改变系统阻尼的情况下可以用较大的增益来加快过渡过程，降低起始误差的具体办法就是根据实际的跟踪目标，设计一个合适的过渡过程，让系统有能力在控制受限的情况下可以追踪这个设计好的过渡过程［14-17］。

定义一个在有限时间内单调平滑上升的函数tran(T0，t):

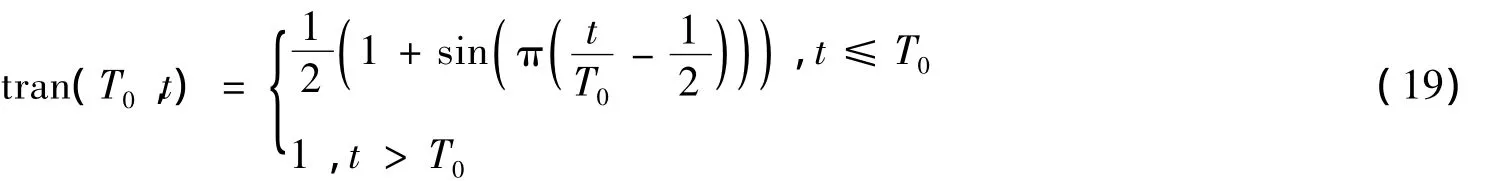
4 仿真结果及分析

4.1 运动仿真

利用式(1)、(2)作为仿真的主体模型，初始条件设为 η0=［0，0，2，0°］T，潜器运动路径设置如下:

首先，从初始点 η0=［0，0，2，0°］T运动到 ηd1=［，5，2，10°］T，并且要求按直线运动，斜率为 30°，然后从 ηd1运动到 ηd2=［5+5，10，2，20°］T，按直线运动，斜率为 45°，整个运动过程保持深度不变。海流速度采用正弦函数模拟vc=0.4sin(0.01t)m/s。仿真时间200 s。控制器参数:Kd=1 000I44，Ki=0.01I44，k=3，过渡时间设为10 s，仿真结果如图2～8。

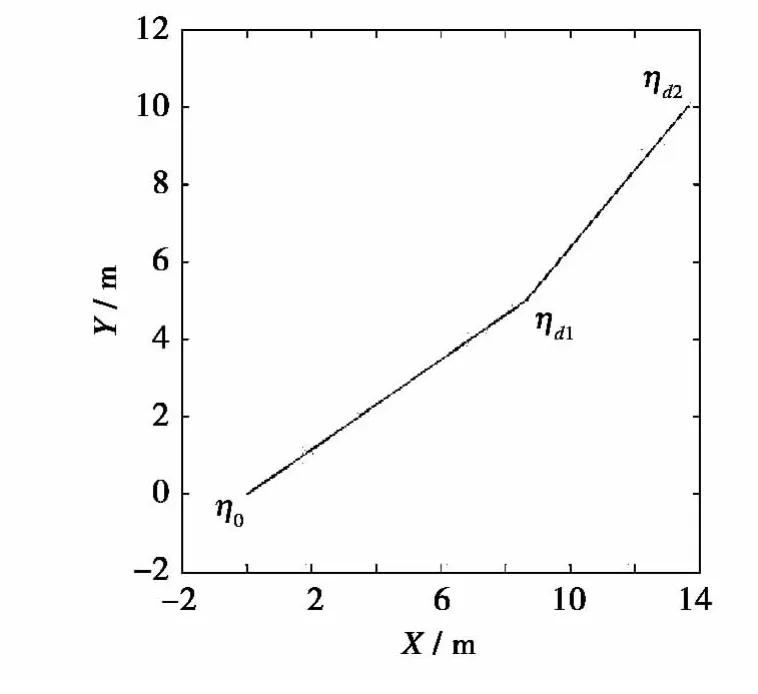
图2 X，Y路径跟踪结果Fig.2 X and Y tracking result

图3 艏向跟踪结果Fig.3 Heading tracking result

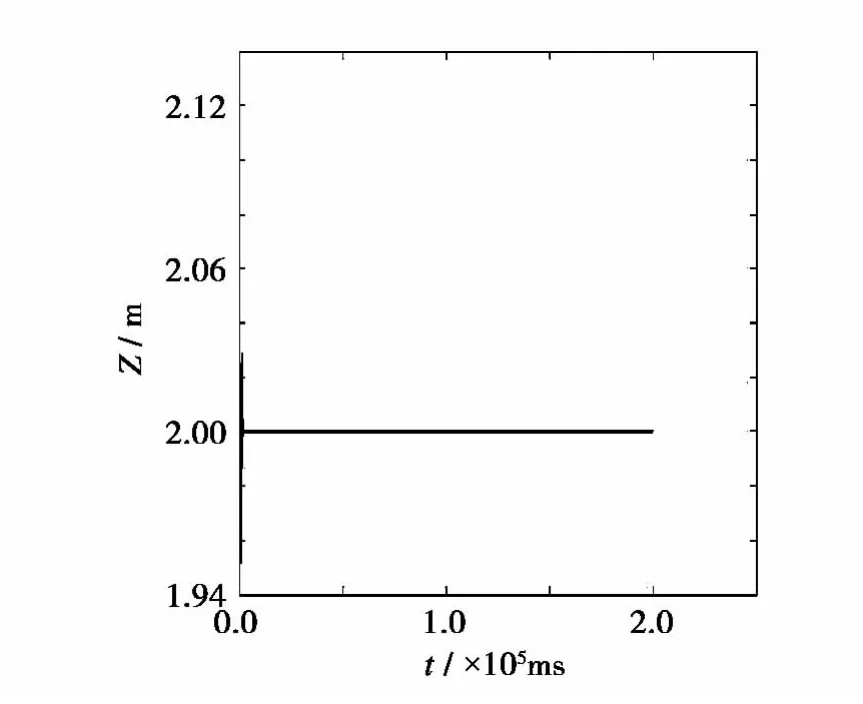
图4 定深控制结果Fig.4 Depth hovering result

图5 X方向推力值Fig.5 X control signal input

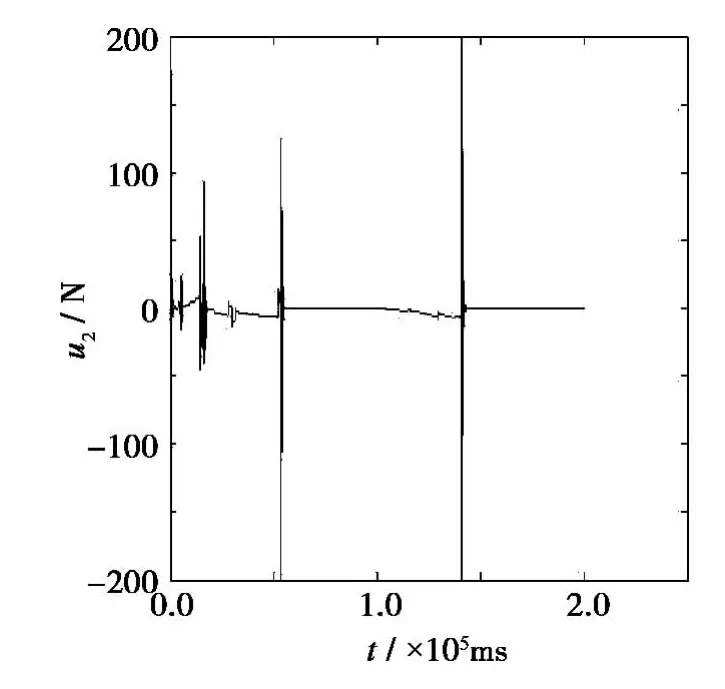
图6 Y方向推力值Fig.6 Y control signal input

图8 艏向扭矩值Fig.8 Heading control signal input

4.2 结果分析

从图2～3可以看出，潜器可以很好地跟踪设定的路径和姿态，并且超调很小，艏向误差在1°左右。从图5～8可以看出，推力和扭矩的输出值比较平稳，这主要由于高阶滑模控制器中的积分项有效的抑制了高频抖振，并且通过过渡过程和变滑模面的设计，有效克服了匹配条件不满足、初始误差比较大的情况。

5 结语

为了解决在水下潜器运动控制中会遇到的潜器模型参数无法准确计算、水流信息无法测量等难题，通过高阶滑模控制器的设计，解决了控制器对模型参数的依赖。合理的过渡过程和变滑模面的设置，保证了系统在任意初始条件下的收敛性和跟踪性能。当无法获取水流信息时，控制器的强鲁棒性保证了跟踪精度，并且系统输出平滑、无抖振，整个算法结构简单，易于工程实际实现，适合工程的实际需要。

［1］ Wonchang Lee，Geuntaek Kang.A fuzzy model-based controller of an underwater robotic vehicle under the influence of thruster dynamics［C］//Proceedings of 1998 IEEE International Conference on Robotics and Automation.1998:750-755.

［2］ Antonelli G，Caccavale F，Chiaverini S，et al.A novel adaptive control law for underwater vehicles［J］.IEEE Transactions on Control Systems Technology，2003，11(2):221-232.

［3］ Cristi R，Papoulias F A，Healey A J.Adaptive sliding mode control of autonomous underwater vehicles in the dive plane［J］.IEEE Journal of Oceanic Engineering，1990，15:152-160.

［4］ 龙建军，吴百海，吴金萍.基于功能原理的水下潜器模型参数辨识方法与实验估计［C］//第二十九届中国控制会议论文集.2010:1195-1200.

［5］ Garcia-Valdovinos L G，Salgado-Jiménez T，Torres-Rodriguez H.Model-free high order sliding mode control for rov:stationkeeping approach［C］//OCEANS 2009，MTS/IEEE Biloxi-Marine Technology for Our Future:Global and Local Challenges.2009:1-7.

［6］ Salgado-Jiménez T，García-Valdovinos L G，Delgado-Ramírez G.Depth control of a1 DOF underwater system using a model-free high order sliding mode control［C］//Electronics，Robotics and Automotive Mechanics Conference(CERMA).2010:481-487.

［7］ Yan Peng，Jianda Han，Qi Song.Tracking control of underactuated surface ships:using unscented kalman filter to estimate the uncertain parameters［C］//Proceedings of 2007 IEEE Internation Conference on Mechatronics and Automation.2007.

［8］ 马 驰，连 琏.水下运载器操纵控制及模拟仿真技术［M］.北京:国防工业出版社，2009.

［9］ Garcia-Valdovinos L G，Parra-Vega V，Arteaga M A.Bilateral cartesian sliding PID force/position control for tracking in finite time of master-slave systems［C］//American Control Conference.2006.

［10］ Parra-Vega V，Arimoto S，Yun-Hui Liu，et al.Dynamic sliding PID control for tracking of robot manipulators:theory and experiments［J］.IEEE Transactions on Robotics and Automation，2003，19(6):967-976.

［11］ Yangmin Li，Qingsong Xu.Adaptive sliding mode control with perturbation estimation and PID sliding surface for motion tracking of a Piezo-Driven micromanipulator［J］.IEEE Transactions on Control Systems Technology，2010，18(4):798-810.

［12］ Parra-Vega V.Decentralized model-free continuous control for robot manipulators:tracking in finite time［C］//Proceedings of the Third International Workshop on Robot Motion and Control.2002:165-171.

［13］ Parra-Vega V.Chattering-free dynamical TBG adaptive sliding mode control of robot arms with dynamic friction for tracking in finite-time［C］//Proceedings of 2001 IEEE International Conference on Robotics and Automation.2001:3471-3476.

［14］韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术［M］.北京:国防工业出版社，2009.

［15］黄焕袍，万 晖，韩京清.安排过渡过程是提高闭环系统“鲁棒性、适应性和稳定性”的一种有效方法［J］.控制理论与应用，2001(S1):89-94.

［16］韩京清.时滞对象的自抗扰控制［J］.控制工程，2008(S2):7-10，18.

［17］韩京清.自抗扰控制技术［J］.前沿科学，2007(1):24-31.