深海管道非线性屈曲理论计算方法
2013-10-11余建星李智博杜尊峰傅明炀卞雪航
余建星,李智博,杜尊峰,傅明炀,卞雪航,杨 源
(天津大学建筑工程学院,天津 300072)
在深水环境条件下,管道一旦出现结构失效,将对工程建设和维修造成重大损失。由于管道在生产制造过程中,其几何尺寸和材料性质的分布存在一定程度的不均匀性,形成管道结构的局部缺陷,使管道在一定压力条件下发生屈曲失稳。在管道的铺设和使用过程中,如果发生碰撞或腐蚀等现象,将进一步增加管道局部缺陷的程度,降低管道屈曲失稳所需的压溃压力。对于大径厚比情况,管道处于小变形的弹性阶段发生屈曲失稳,此时的几何变形和材料本构皆为线性关系。然而,对于小径厚比情况而言,发生屈曲失稳时几何变形和材料本构皆可能处于非线性阶段。对于存在初始缺陷的情况,其与径厚比的耦合影响,更使得管道的屈曲失稳表现为明显的非线性特征。
周承倜[1]对海底管道的屈曲进行了研究,介绍了8种不同控制屈曲发生的屈曲压力。Fabian[2]对弹性范围内管道在弯矩和轴向拉力联合作用下的非线性屈曲响应进行过分析。Wilhoit[3]等研究了管道在弯矩和轴向拉力联合作用下的弹塑性响应,但未考虑加载路径的影响。Palmer[4]于1975年首次揭示深水管道铺设过程中,管道的局部屈曲失稳会导致屈曲沿管道轴线传播的现象。Bai[5]应用有限元软件分析了管道在外压、轴向拉力和弯矩共同作用下的屈曲性能,并进行了初始椭圆度、残余应力、应变硬化和加载路径的敏感性分析。Dama[6]通过试验和数值模拟研究了受损管道在内压和弯矩作用下的承载力,以及在交变荷载作用下的疲劳剩余寿命预测,为局部屈曲受损管道的继续使用提供了安全评估基础。Toscano[7]等人建立了三维有限元模型,分析了深水海底管道整体式止屈器的穿越压力和机理,并与试验结果进行对比。Xue[8]应用ABAQUS软件分析了非均匀和受腐蚀海底管道在外压作用下的屈曲和屈曲传播特性,发现了管道对称和反对称屈曲模态主要与管道截面不均匀部分的相对厚度和角度有关。Estefen[9]通过小比例试验结合薄壳理论分析评估了完好管道在外部静水压力和弯矩作用下的极限强度,以及受损管道在外部静水压力作用下的剩余强度。Kyriakide.S[10]等对管道的屈曲问题进行了研究,分析了径厚比、材料特性、初始椭圆度和加载路径对管道局部屈曲的影响。综上所述,在深海管道屈曲方面,国内研究较少,且较国外尚有较大差距。针对海底管道屈曲过程中的几何非线性和材料非线性因素,建立屈曲准则,利用虚功原理求解含椭圆度缺陷的管道屈曲变形及其临界压力,分析其影响规律,并进行全比例试验和用有限元模拟进行验证,取得很好结果。此分析方法为我国深海油气开发的安全保障提供理论支持,为进一步深入研究屈曲传播和止屈技术奠定基础。
1 理论模型
管道在外压作用下发生椭圆度变形。对于沿轴向具有缺陷程度近乎相同的较长管道而言,在其前屈曲阶段,这种椭圆度变形沿轴向几乎是一致的,直至缺陷程度略微大于其它截面的部位首先发生屈曲失稳为止。管道压溃压力的确定,与失稳之后的后屈曲阶段无关,仅取决于轴向变形一致的前屈曲阶段,可以以某一截面的变形代替管道整体的变形。故此,建立二维环模型,如图1所示,并基于以下假定:
1)管壁厚度沿环向均匀分布;
2)圆环的弯曲变形满足平断面假定;
3)圆环径向应力与其环向应力相比较小,可以忽略不计;
4)考虑材料的弹塑性本构关系;
5)认为在变形过程中,材料保持各向同性;
6)管道长度足够长,端部约束条件的影响可以忽略;
7)考虑截面上存在沿轴向一致的轴向应力和轴向应变的影响;
8)管道压溃时,截面发生双凹形变形。
坐标系的建立包括整体笛卡尔坐标系和局部曲线坐标系。曲线坐标系取圆环变形前的构形作为参考,v,w分别表示环向和径向的位移分量,R为变形前的中性面的半径,管壁的中性面上各点由坐标R,θ表示,如图2所示。

图1 管道变形截面示意Fig.1 Cross-section pipe deformation

图2 中性面位移的定义Fig.2 Definition of the neutral plane displacement
2 基本方程
2.1 几何方程
将环向应变ε0分为薄膜应变和弯曲应变 κθθ两部分的叠加:

其中,z为中性层法向坐标(m)。薄膜应变和弯曲应变分别为:
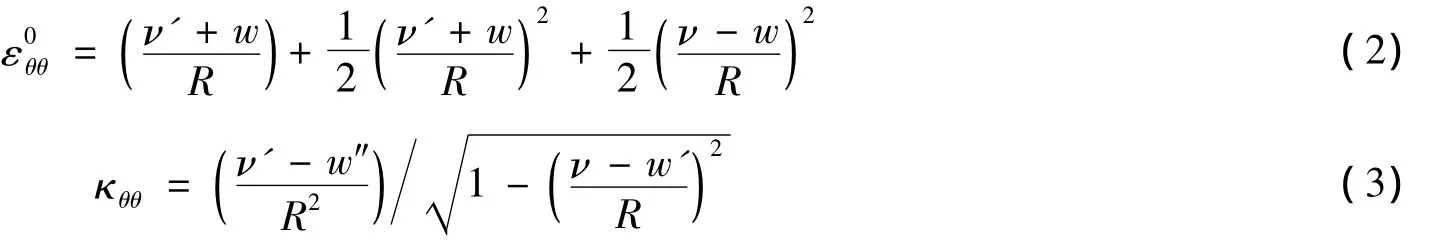
2.2 本构方程
管道的本构关系采用基于J2塑性流动理论的弹塑性模型。
各向异性的屈服函数:

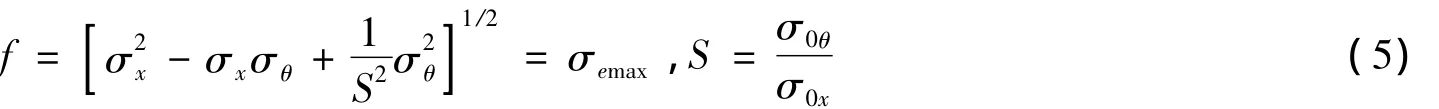
2.3 能量方程
根据虚功原理,管道的平衡方程可以表达成如下形式[10]:


外力功增量的变分 为外压在管壁变形方向作功沿环向的积分

3 数值离散
3.1 定解条件
1)边界条件
在变形过程中,管壁的位移函数ν、ω需满足对称的边界条件:

2)初始条件
屈曲失稳因结构本身或施加载荷的非均匀性而导致。在本模型中,载荷的施加和材料特性具有对称性和各向同性,因此,需要在初始条件中赋予结构一定的几何缺陷,即初始椭圆度。当初始椭圆度为极小值时,代表实际中截面为圆形的管道屈曲情况。
假设管道具有轴向统一的初始椭圆度Δ0(Δ0=a/R),此时中性面上沿环向各点的径向初始位移¯w和环向初始位移:


由此,在变形过程中任意质点处的环向应变表达式改写为:

3.2 位移函数
假设管道的屈曲为椭圆化屈曲,根据截面变形的边界条件,则位移函数可写成三角级数的展开式形式:

位移函数展开式形式和阶数,在很大程度上影响着分析结果的精度。
3.3 非线性方程组
将位移离散函数代入几何方程、本构方程,可得到离散形式的应力、应变表达式。对于每个载荷步,利用虚功原理,将离散形式的能量方程对各个位移函数参数求变分,可得一组非线性方程组,如式(14)所示。每个载荷步下,此方程组的平衡对应着结构的静力平衡状态。
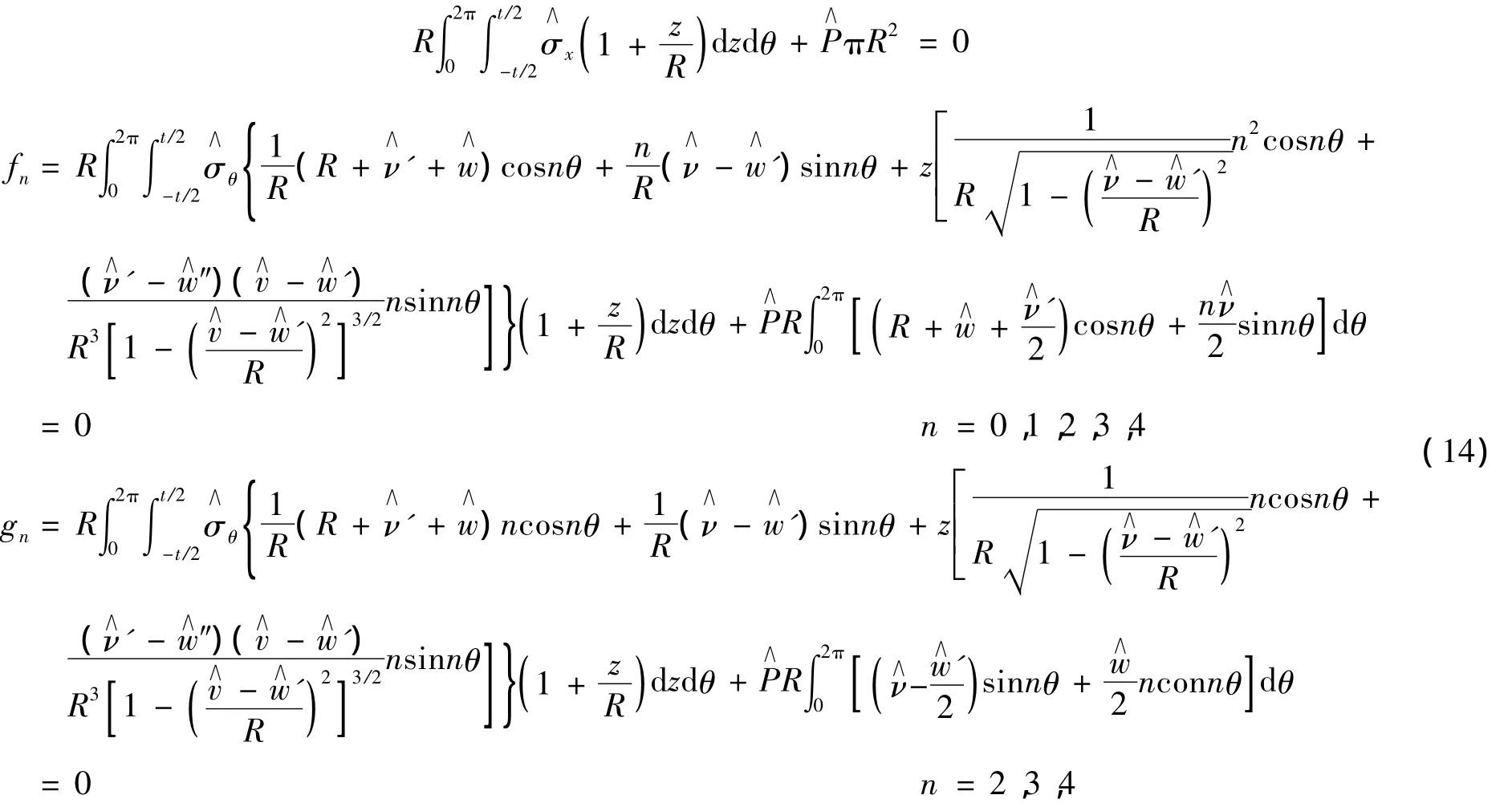
4 求解和分析
4.1 计算求解
根据初始缺陷所对应的管道结构参数,进行准静态的增量加载,直至管道最大径向位移随压力的增加而开始降低为止。基本流程如图3所示。
4.2 理论分析与有限元分析、压溃试验及DNV规范的对比
管道的ABAQUS有限元模型采用C3D8I单元,这样相比于壳单元可以沿壁厚方向划分更多的网格,以提高分析精度。考虑对称性建立管道模型,在管道两端施加全固端约束,在圆柱壳的外表面施加均布压力。根据理论分析得到压溃压力值,设定一个高于此值的压力,运用RIKS方法进行分析计算。图4所示为节点位移云图;图5所示为管道模型的加载压力与管道被压缩体积之间的关系曲线,图中压力的峰值即为管道的压溃压力。
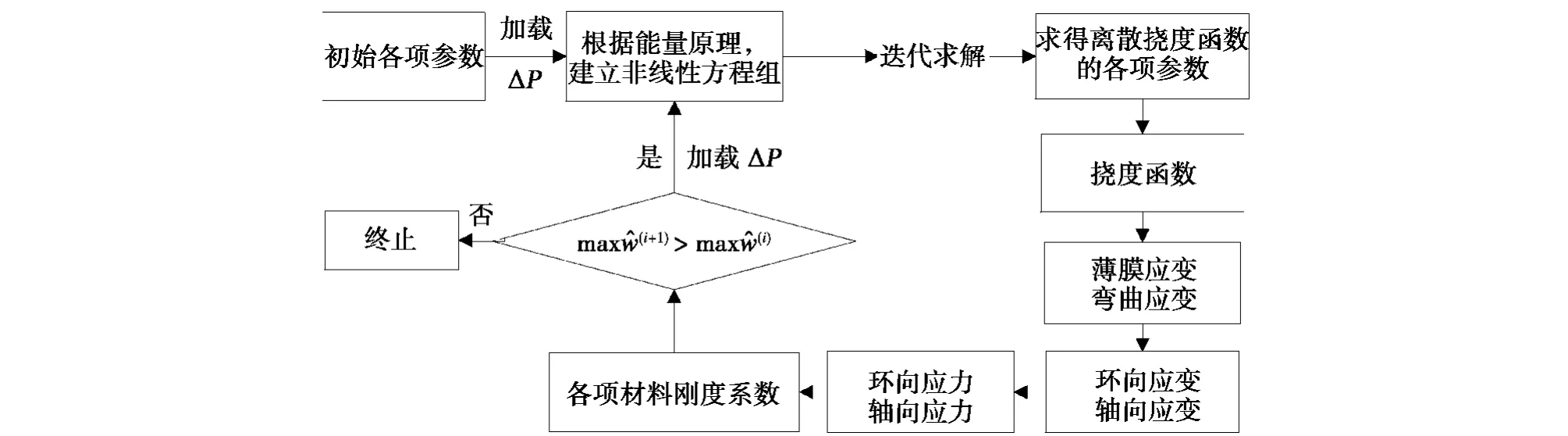
图3 分析流程示意Fig.3 Analysis process

图4 节点位移云图Fig.4 Nodal displacement cloud
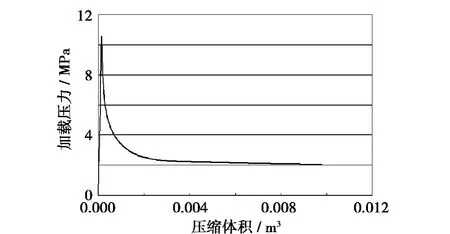
图5 加载压力随管道压缩体积变化的曲线过程Fig.5 Curve of the compressed pipe volume with the load
在进行理论分析和有限元分析的同时,进行了管道屈曲压溃试验,试验结果可与前者进行对比验证。试验采用等比例模型,压力舱体内部可容纳8 m长的管道试件。试件两端约束条件为固支,试件外直径为16英寸(约406 mm)和12英寸(325 mm)两种。通常,海底管道的屈曲行为与以下因素有关:轴向载荷、环境温度、边界条件、初始缺陷、静水压力等。对于管道这种薄壁结构而言,当其处于中空状态时最有可能在外部载荷作用下发生屈曲,这是最危险的情况。由于实际的海底管道表面要敷设保温材料,可以认为这种状态下管道内部的温度是恒定的,而且海水环境温度也可以视为恒定值。因此,本试验中的工况为管道内部中空,端部固支,外部逐渐加载静水压,未加载轴力和弯矩,不考虑温度变化对管道屈曲行为的影响。
图6为试验管件压溃前后的形状对比,可见压溃后管件变形非常严重,管件变形中间最扁,两端过度逐渐变形变小。

图6 试验管件压溃前后对比Fig.6 Comparison of test tube before and after collapse
通过压溃试验,深水海底管道屈曲试验测试系统得到了加压试验的压力增加过程,从中可以看到压力从增加到临界载荷瞬时降至接近零的全过程,其最高点即为管件的临界载荷,如图7所示。
将管道尺寸为325×10、406×10、325×6(mm)的三种管道的压溃压力理论结果与有限元模拟结果、试验结果、规范计算结果进行比较。管材规格为API-5LX65,弹性模量 E=2.06×1011Pa,屈服极限 σ0=448 MPa。结果如表1所示。表中的初始椭圆度值和试验结果均为对三种尺寸管道进行多次管件试验的平均统计结果。
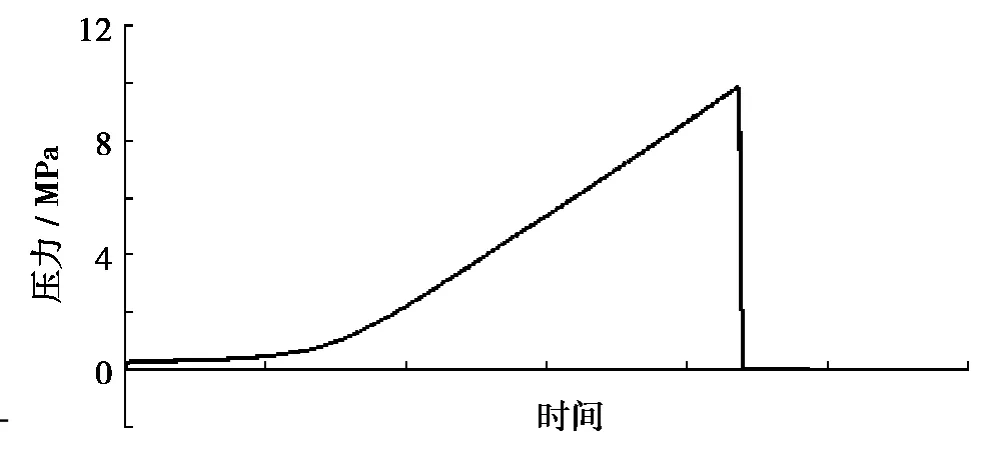
图7 试验中压力随时间加载曲线Fig.7 Curve of test pressure load with time

表1 分析结果对比Tab.1 Comparison of the results of different motheds
从表1中可以看出,理论计算方法的压溃压力与试验结果、有限元模拟及规范值都很接近,证明理论计算方法的计算精度的可靠性。
4.3 椭圆度对压溃压力的影响
采用理论分析方法,对径厚比在10~55之间的五种管道在不同初始椭圆度缺陷情况下的压溃压力进行计算。计算分析结果表明:管道压溃压力随径厚比的增加和椭圆度缺陷程度的增大而下降,不同的径厚比受椭圆度影响程度不同,计算结果如图8所示。对于径厚比为54.17、40.64、32.5、20、10五种情况,椭圆度为0.5%时,压溃压力相对于无初始椭圆度分别下降13.3%、20%、26.7%、16.2%、5.5%。

图8 不同径厚比的管道的压溃压力-椭圆度曲线关系Fig.8 Curve of collapse pressure with initial ovility
5 结语
在考虑轴向均匀一致变形的情况下,建立基于圆环的管道力学模型,利用虚功原理建立平衡方程,选用合适的位移离散函数进行方程离散并数值求解,得到含椭圆度缺陷的管道均匀压溃的前屈曲阶段变形响应及压溃压力。通过试验、有限元分析结果、规范对其进行对比验证,计算了不同椭圆度对压溃压力的影响。分析结果表明:1)该方法的计算结果精度可靠,适用于对深水管道的屈曲压溃强度评估;2)在该方法中,位移离散函数形式、阶数的选取和管道材料本构关系影响最终结果的准确性,对这两者的选取要尽量精确;3)沿轴向分布一致的椭圆度缺陷对管道的压溃压力有明显影响,减弱程度因不同径厚比而异,上述计算曲线为工程应用提供参考。
[1] 周承倜,马 良.海底管道屈曲及其传播现象[J].中国海上油气,1994,6(6):1-8.
[2] Fabian O.Collapse of cylindrical elastic tubes under combined bending pressure and axial loads[J].International Journal of Solids and Structures,1977,13:1257-1270.
[3] Wilhoit J C,Merwin J E.The effect of axial tension on moment carrying capacity of line pipe stressed beyond the elastic limit[C]∥Proceedings of the Offshore Technology Conference.1971:OTC1335.
[4] Palmer A C,Martin J H.Buckle propagation in submarine pipelines[J].Nature(London),1975,254:46-48.
[5] Bai Yong,Bai Qiang.Subsea Pipelines and Risers[M].Oxford:Elsevier Science Ltd,2005.
[6] Dama E,Karamanos S A.Failure of locally buckled pipelines[J].ASME,Journal of Pressure Vessel Technology,2007,129:272-279.
[7] Toscano R G,Mantovano L O,Amenta P M,et al.Collapse arrestors for deepwater pipelines[J].Cross-over Mechanisms,Computer& Structures,2008,86:728-743.
[8] Xue Jianghong.A non-linear finite-element analysis of buckle propagation in subsea corroded pipelines[J].Finite Elements in Analysis and Design,2006,42:1211-1219.
[9] Estefen S F.Collapse behavior of intact and damaged deepwater pipelines and the influence of the reeling method of installation[J].Journal of Constructional Steel Research,1999,50:99-114.
[10]Kyriakide S,Corona E.Mechanics of Submarine Pipelines[M].Oxford:Elsevier Science Ltd,2007.
