海洋管道单点提放的若干数学模型研究
2013-10-11曾霞光段梦兰陈景皓
曾霞光,段梦兰,陈景皓
(中国石油大学(北京)机械与储运工程学院,北京 102249)
随着中国深海油气开发的进程,中国必须掌握深水管道铺设和安装的分析设计技术。深水海洋油气开发中,主要的铺管安装方式有S型铺设,J型铺设等。铺管和安装作业中,回收和弃置管道操作非常普遍。在这些作业过程中,管道的轴力,弯矩,应力,应变等需要控制在一定的范围内以保证管道完好,因此海洋管道铺设和收弃作业方案,尤其是船舶位置移动设计和缆绳的收放速度非常重要。为了进行设计分析,需要建立海洋管道的收弃作业过程分析模型和方法。
铺管作业可以看作弃管作业的前期工作或者收管作业的后期工作,因此用于分析的力学模型与收弃管分析模型相同。弃置时海洋管道通常将脱离托管架或其他支撑结构,A&R绞车的钢绳通过海洋管道封头将管道从海面缓慢下放到海底,回收时A&R绞车的钢绳通过海洋管道封头将管道从海底缓慢拉升到海面上,此过程被称为海洋管道的单点提放。在这个往复过程中,管道经历了一个大变形和小变形相互转化的变形过程。
1 控制微分方程
海洋管道从海底提升到海面或者从海面下放到海底,这两个物理过程是互逆的,可以用同一个数学模型进行描述。在管道提放作业时通常要求海洋环境平稳,管道提升或者下放速度缓慢,因此可把问题处理成静态问题。另外可认为海底为刚性水平面[1],海洋管道由各向同性材料组成,且提升和下放过程中始终处于弹性状态。在上述条件下,不考虑海水流动效应,取悬空管段进行研究,如图1所示。以悬空管道与海床的接触点(触地点)为原点o,建立笛卡尔坐标系。再沿管线建立自然坐标系,显然该管线上的物理量均为管线弧长的单变量函数。令管道与水平方向的夹角为θ,长度为L,材料弹性模量为E,截面惯性矩为I,水中的单位线重为w,上端点受拉力T0作用,与水平方向成夹角θ0,管线原点处横截面的水平力为H0,铅垂力为V0。其中铅垂力V0的可能来源有且仅有两个,一个是左边管道对其剪力,另一个是刚性接触海床对其向上的支撑力。由于通常认为左边管道没有弯曲变形,其弯矩为零,因此其相互剪力也为零,否则左边管道必然弯曲。由此可知原点处的铅垂力就是刚性海床对其向上的支撑力。
根据文献[2-5],如图1所示的海管提放问题可以用如下微分方程描述:
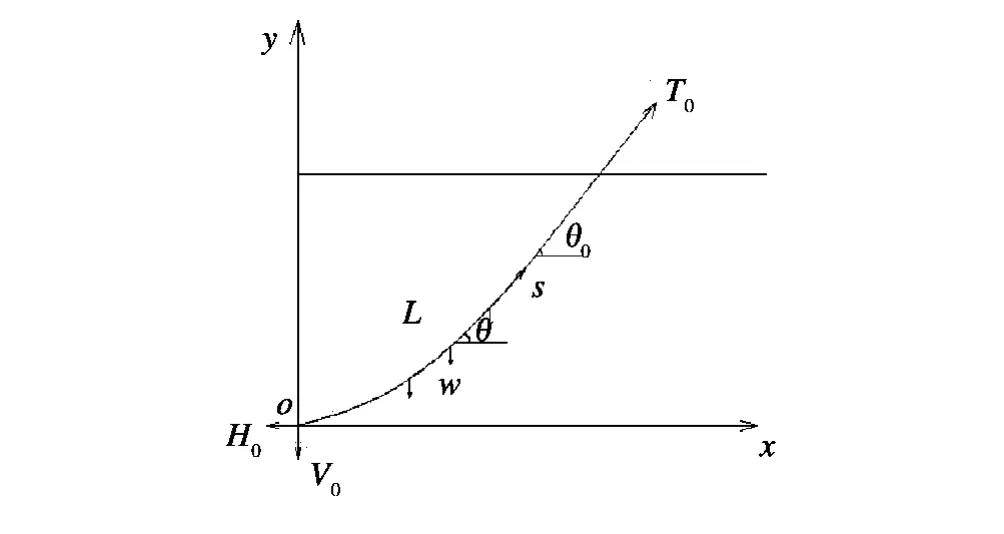
图1 管道单点提放力学模型Fig.1 Mechanical model of pipe lifting or lowering by one point
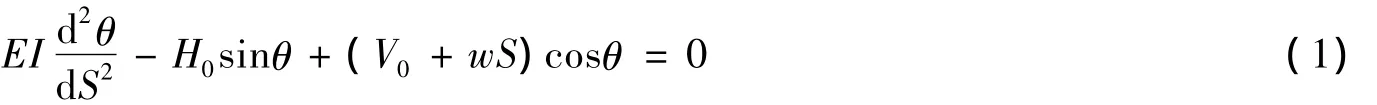
根据水平和垂直方向上力的平衡有:

将式(2)、(3)代入方程(1)得:

根据文献[6],该问题也可以用以下控制微分方程组描述:

用这两种微分方程对管道收放问题进行分析,结果差异何在?这两种控制微分方程是否都能很好地描述海洋管道的提放过程?哪种微分方程更好地描述海洋管道的提放过程?为了回答上述及相关问题,将以两种微分方程为核心建立海洋管道提放过程的三个分析模型,并借助数值计算方法分别进行求解,然后对计算结果进行分析。
2 边界条件
分析海洋管道提放过程中边界处的形态和受力情况,通常认为有如下边界条件[3,5-7]:
触地点处:挠度 y(0)=0,转角 θ(0)=0,水平力 H0=T0cosθ0,弯矩 M(0)=0。
上部端点处:弯矩M(L)=0,拉力为T0。
3 悬空管道长度
悬空管道长度L是求解本问题的关键参数,不能预先确定。文献[1]认为刚性海床情况下提起段长度等于2倍的提升力除以管道线重,文献[2-3]根据几何条件确定悬空管道长度,而文献[5-8]都用各自的迭代方法确定该参数。与这些方法不同,将根据力学原理提供一个新的确定悬空管道长度的公式。
考虑悬空管道的外力对管道上部端点的弯矩,根据弯矩平衡原理有:

将式(2)、(3)代入式(6)得:

式(7)中只有一个独立未知量变量L,L一旦确定,x(L),y(L)和x(S)就随之确定,因此可以求解该方程来确定悬空管道长度。求解方法是迭代法,思路为不断假设一个悬空管道长度L,求解以式(4)或式(5)为控制微分方程的定解问题得到管道形态,直到下式成立:

此时即可认为该长度就是管道悬空长度,其中ε为迭代计算误差限。
4 数学模型
取微分方程(4),选择如下边界条件:触地点处的转角为零,上部端点处的弯矩为零,再结合式(7),得到分析模型1,即:

取微分方程(4),选择如下边界条件:触地点和上部端点处的弯矩都为零,再结合式(7),得到分析模型2,即:
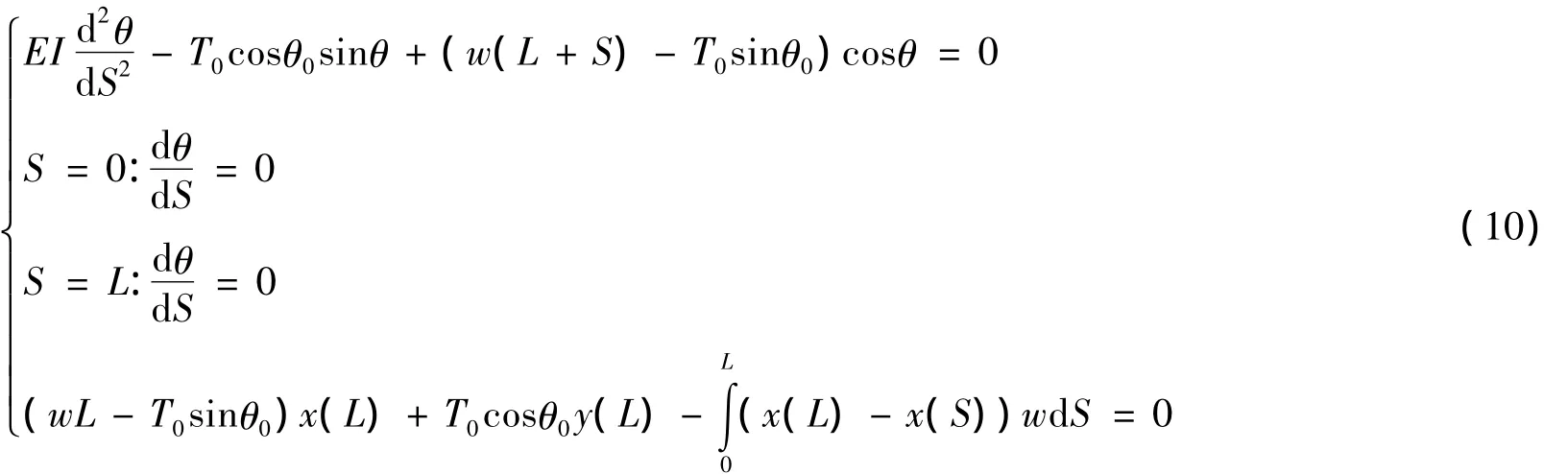
取微分方程组(5),选择如下边界条件:触地点处的转角为零,弯矩为零,水平力为T0cosθ0,上部端点处的弯矩为零,再结合式(7),得到分析模型3,即:

5 数值求解算例及结果分析
模型1和模型2的未知函数是θ(S),模型3的未知函数是θ(S)和T(S),由于上述微分方程均是高度非线性方程,无法得到其解析形式的解。为了分析这些模型的差异,并找出准确描述海洋管道提放物理过程的数学模型,下面对它们进行数值求解。
采用MATLAB作为求解环境,利用其中的内置函数bvp4c[9]求解如表1、2所示的一组具体参数对应的分析模型1、2和3,计算结果如图2所示。

图2 不同拉力作用时管道的转角、形态和弯矩Fig.2 Angle,configuration and bending moment of pipe loading under different tension
从计算结果图2中可以发现以下主要特点:
1)模型3确定的悬空管道长度在三个模型中是最大的,模型2确定的悬空管道长度最小;
2)模型1的弯矩极值在三个模型中是最大的,发生在触地点处,模型2的弯矩极值总是最小,模型2和3的弯矩极值都不发生在触地点处;
3)弯矩极值随着悬空管道长度的变化而变化,其先随悬空管道长度增加而增加,之后随悬空管道长度增加而减小,最大值发生在悬空管道约100 m处;
4)随着载荷增大三个模型的解越来越接近,在悬空管道长度小于1 000 m时,三个模型的转角、形态和弯矩的结果差别较大,且长度越小差别越大。在悬空管道长度大于1 000 m时,模型2和模型3的转角、形态和弯矩的计算结果几乎相同,但是模型1的结果与其它两个模型在弯矩的极值及其发生位置存在较大差异;
5)从图2(a)~(d)中可以清楚看出,模型1的弯矩极值发生在触地点,这与实际情况矛盾,而模型2在触地点的转角值也与该问题的边界条件矛盾。

表1 材料几何参数Tab.1 Geometrical and material parameters

表2 载荷参数Tab.2 Loading parameters
根据计算结果的特点,可以初步判定描述海洋管道提放全程的数学模型应该采用分析模型3。为了进一步证实该模型的正确性,作者以分析模型3为理论模型,编写开发了海洋管道提放静力学分析软件DRICAS,采用上文中的管道材料几何参数,重新计算了如表3所示载荷情况下的管道形态。

表3 载荷参数Tab.3 Loading parameters
将其形态计算结果与专业海洋工程有限元分析软件OrcaFlex的计算结果进行对比,可以看到两者的计算结果在各个载荷情况下都是一致的,如图3所示。这进一步证实了模型3的正确性。

图3 DRICAS和OcraFlex形态结果对比Fig.3 Configuration results comparison between DRICA and OcraFlex
6 结语
通过三个模型的数值求解和分析表明:
1)对海洋管道缓慢单点提放进行全程分析宜采用模型3,它能准确描述管道提放的完整过程;其中该问题的边界条件是触地点处水平转角为零,弯矩为零,受到提升载荷水平分量大小的拉力,上部端点处弯矩为零;另外悬空管道长度可以根据弯矩平衡原理确定。
2)因为弯矩极值位置不合理,模型1不能准确描述海洋管道单点提放过程并用于管道的力学分析。
3)悬空管道长度小于900 m时,模型2不能准确描述海洋管道单点提放过程;悬空管道长度大于1 000 m时,模型2与模型3计算结果的相对误差很小,且悬空管道越长相对误差越小,因此在悬空管道长度大于1 000 m时可用模型2代替模型3,从而减少计算机数值计算时间。
4)弯矩极值随着悬空管道长度变化而变化,其先随着悬空管道长度增加而增加,之后随着悬空管道长度增加而减小,最大值往往发生在管道提升过程的中前期或者下放过程的中后期。
[1] 邢静忠.海底管道离地点的接触条件探讨[J].力学与实践,2005,27(5):57-60.
[2] 宋甲宗,戴英杰.海洋管道铺设时的二维静力分析[J].大连理工大学学报,1999,39(1):91-94.
[3] 戴英杰,宋甲宗,冯 刚.海底管道收弃管作业分析[J].海洋工程,2000,18(3):75-78.
[4] 邢静忠,柳春图,曾晓辉.海洋石油管道单点提升分析[J].海洋工程,2002,20(3):29-33.
[5] 曾晓辉,柳春图,邢静忠.海底管道铺设的力学分析[J].力学与实践,2000,24(2):19-21.
[6] Charles P.Sparks.Fundamentals of Marine Riser Mechanics[M].Tulsa,Oklahoma:PennWell,2007:254-256.
[7] 詹 侃,陆仁华.海底管道在铺设过程中的二维静态分析[J].海洋工程,1991,9(4):14-20.
[8] 帅 健,吕英民,张进国.用动坐标迭代法分析海洋管道敷设时的应力[J].油气储运,1996,15(10):21-24.
[9] Shampine L F,Gladwell I,Thompson S.Solving ODEs with MATLAB[M].New York:Cambridge University Press,2003:133-211.
