选粉机颗粒轨迹的非稳态模拟
2013-10-11李双跃
童 聪,李双跃,李 翔
(1西南科技大学制造科学与工程学院,四川 绵阳 621010;2西南科技大学应用技术学院,四川 绵阳 621010)
选粉机是粉体制备系统中的重要设备之一,它能将粉体中合格的细粉分选出来作为成品,同时将不合格的粗粉返回粉磨装置重新粉磨。对选粉机分级性能的研究是当前国际上的一个研究热点,具有重要的工程应用价值[1]。
已报道的研究中,Roland等[2-3]运用涡流分级理论研究设计了新转笼结构选粉机;Guo等[4]对选粉机流场进行了测量,考察了转子径向及轴向速度分布;Finch[5]、Nageswararao 等[6]对 Tromp曲线“鱼钩效应”进行了理论分析及实验验证;刘家祥等[7]对分级转子内“惯性反旋涡”现象进行了阐述,提出了改进方案,并对分级功能区域、壳体内湍流涡频谱特性和流场特性进行了理论分析和实验研究。黎国华[8]、杨庆良[9]和黄强[10]等对选粉机气相流场进行了数值模拟,研究了选粉机流场特性;杜妍辰等[11]以单颗粒动力学模型对分级室二维平面颗粒运动轨迹进行了模拟分析;Xu等[12]对转子叶片间流场模型进行了单粒径颗粒束轨迹模拟。查阅文献发现,已有的模拟研究多针对速度场[8-10]、压力分布[13-14]等间接因素来评价选粉机分级性能,对细粉颗粒质量流率和粒径分布等直接因素的考察分析较少;对颗粒运动的分析多在稳态下追踪单颗粒或单粒径颗粒束轨迹,计算结果以颗粒平均轨迹[15]来描述,在工程应用中具有一定的局限性,因为选粉机内存在数量大和粒径分布广的颗粒群,颗粒在外力(如重力、气体曳力和离心力)作用下,可展现出颗粒对流运动和尺寸分离等许多复杂的个体行为和集体行为[16],各颗粒存在相对独立的运动轨迹。
本文以SLK选粉机为研究对象,应用离散颗粒模型(DPM)和非稳态(unsteady)模拟方法对颗粒轨迹进行了模拟研究。运用模型的颗粒运动方程对时间积分求解颗粒运动轨迹,旨在研究颗粒的分级过程,并对不同工况下粗、细粉颗粒质量流率与细粉颗粒粒径分布情况进行分析。
1 计算模型
1.1 物理模型
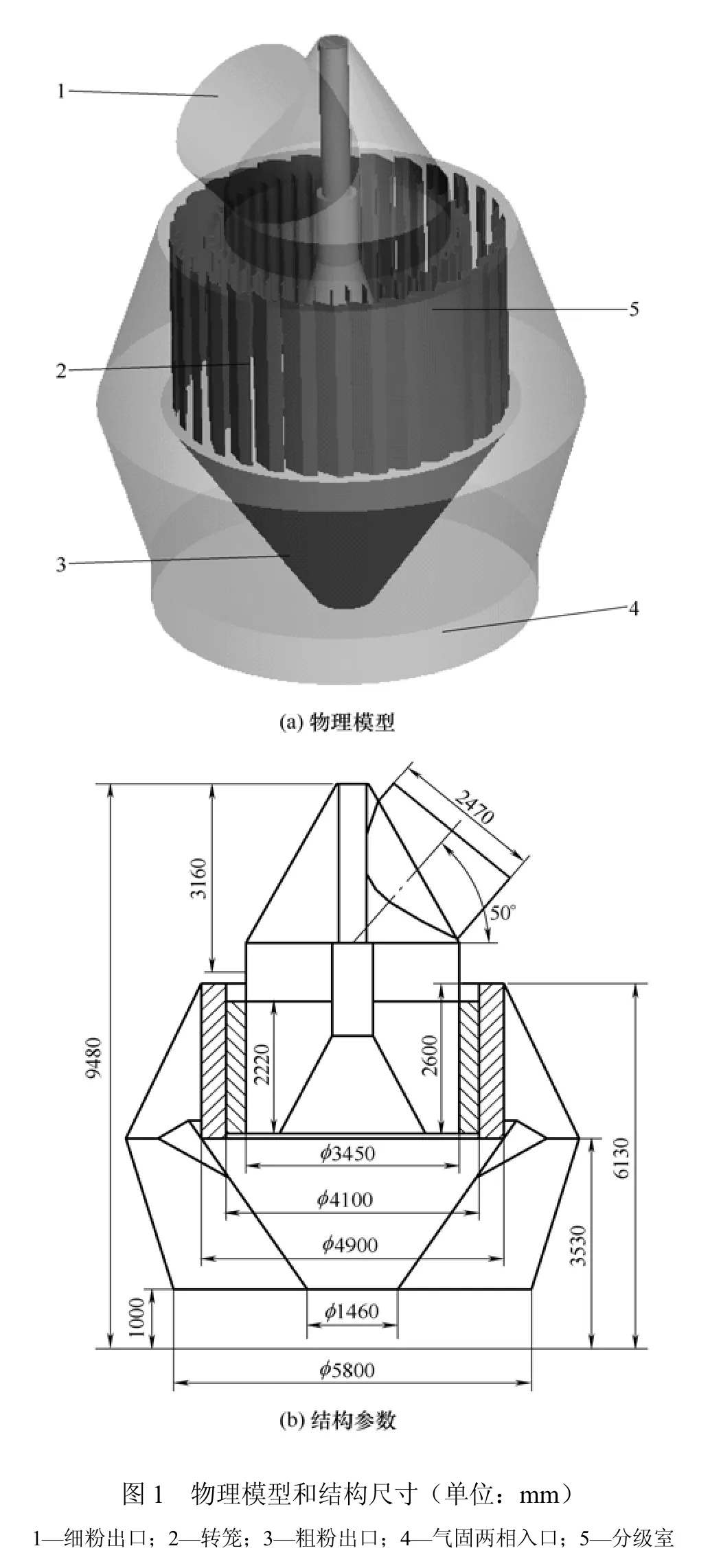
以SLK 5500选粉机为研究对象,其正常工作时分级粒径为40~60 μm,分级精度为0.4~0.7,牛顿分级效率在60%~90%之间。其工作原理如图1(a),气固两相流从选粉机底部进入,分级室内由转子转动形成强旋流场。粗、细粉因在转子外缘的受力大小不同而实现分离,细粉受到气体曳力大于离心力,进入转子内部后经细粉出口排出,粗颗粒受到的气体曳力小于离心力,沿转子径向向外运动与壳体碰撞后失去动量,从粗粉出口排出。
根据如图1(b)所示实际参数建立流场计算模型并进行网格划分,对转子叶片和分级室等关键部位网格加密。转子叶片内外区域采用独立网格划分,利用滑移网格(moving mesh)技术处理叶片内外网格相交面耦合,并将叶片区内外相毗邻的面设定为交界面(interface)。经网格无关性[17]验证,选粉机进出口压差、成品产量等参数不再随网格数量而变化,最终网格数量为682423,网格最大畸形值为0.79。
1.2 边界条件
选粉机气相入口为速度入口(velocity-inlet),气流速度值根据入口风量换算,气相出口为自由出口(outflow)。颗粒喷射源为面域喷射(surface),由气相入口平面与气流以相同速度喷射,质量流率为60 kg/s。细粉出口和粗粉出口离散相边界条件为逃逸(escape),其它壁面为反弹(reflect)。
离散相颗粒尺寸分布根据实况采集数据按Rosin-Rammler分布[18]拟合,见式(1)、式(2)。
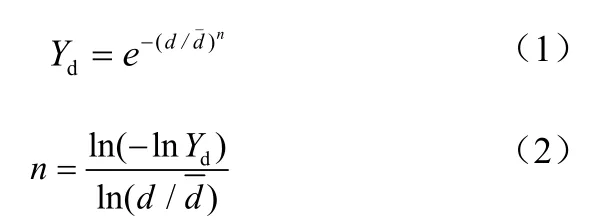
式中,Yd为大于粒径d的颗粒质量分数;为尺寸分布的平均粒径;n为尺寸分布指数。入口颗粒尺寸分布曲线如图2所示,根据式(1)、式(2)计算结果,定义入口颗粒喷射源:最小粒径为1 μm,最大粒径为600 μm,平均粒径为60 μm,分布指数为0.81,颗粒按上述分布参数共定义120组进行计算。
2 数值模拟
2.1 气相流场计算

定义6组不同水平的风量和转速工况点进行模拟计算,参数设置见表1。其中工况1~3转速(N)统一定义为60 r/min,风量(W)分别为4500 m3/min、5500 m3/min、6500 m3/min;工况4~6风量统一定义为5500 m3/min,转速分别为45 r/min、55 r/min和65 r/min。

表1 模拟计算工况点参数设置
以稳态算法首先对气相进行单相计算,湍流模型运用重正化群理论的RNGk-ε湍流模型[19],离散方程选用SIMPLE算法求解压力-速度耦合,选粉机内部为强旋流动,具有各向异性[20],且分级室内外压力梯度较大,压力插补选用PRESTO!格式,对流项采用一阶迎风格式计算,计算收敛精度为10−5。
2.2 颗粒轨迹的非稳态模拟
稳态算法求解气相流场收敛后,作为颗粒相计算的初始场。运用离散颗粒模型(discrete particle model)来模拟颗粒释放,采用非稳态(unsteady)方法追踪颗粒轨迹。用DPM模型的颗粒运动方程对时间积分求解颗粒运动轨迹,时间步长取0.2 s。颗粒轨迹方程以及描述颗粒质量传递的附加方程都是在离散的时间步长上逐步进行积分运算求解的。颗粒的轨迹可由式(3)计算。

沿各坐标方向求解上述方程即可得到离散相颗粒轨迹,其轨迹方程可以简写为式(4)。

应用梯形差分格式对(4)积分,可得式(5)。

式(5)中,n代表第n次迭代步,并且可有式(6)、式(7)。
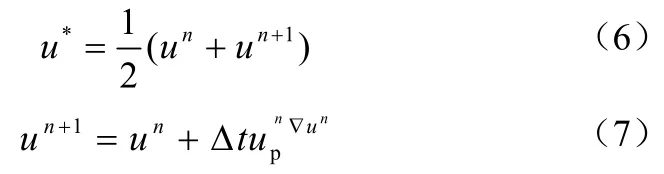
在给定时刻,同时求解式(3)和式(4)可确定颗粒的速度与位置。每隔若干个气相流场迭代时间步,对每个颗粒进行一轮包括一步或多步的轨迹计算和源项计算,从而将颗粒逐轮,逐步地沿轨迹向前推进,依次得到每一步计算后更新的颗粒状态(位置、速度、尺寸等)。非稳态方式得到某一时刻全部颗粒的当前状态,及颗粒的当前位置。
2.3 颗粒质量流率计算
颗粒完成分级的过程实质是粗、细粉分别被不同平面捕集,从而停止轨迹计算的过程。细粉出口平面为离散颗粒escape边界,当颗粒轨迹追踪到此处,颗粒被标记为“escaped”,并终止其轨迹计算。非稳态计算过程中,以时间步为周期更新细粉出口捕集的颗粒质量。若第n个时间步计算完成后更新的细粉颗粒质量数值为Qn(单位kg),第n+1个时间步计算完成后更新为Qn+1,则细粉颗粒质量流率为相邻两时间步长细粉颗粒质量之差与时间步长比值,见式(8)。

式中,q为质量流率,kg/s;Δt为时间步长,s。以此类推,根据连续时间步计算结果,可绘制细粉颗粒质量流率随时间变化的曲线,粗粉颗粒质量流率计算方法同理。
2.4 细粉颗粒粒径分布计算
计算中,对细粉捕集平面进行颗粒轨迹采样(sample)。触发颗粒轨迹跟踪计算开始后,当颗粒与细粉出口平面相交时,其当前状态信息如颗粒位置、各分向速度、粒径和温度等,被记录到采样文件中。采样文件因颗粒数量大,信息复杂,需进行信息归纳处理计算。以粒径相同的颗粒为同类项合并,可得到各粒径颗粒的数量百分数。在工程应用中,考察细粉颗粒粒径数量分布意义较小,故根据细粉颗粒数量和粒径计算出相应的体积(或质量)加权百分数,用颗粒粒径分布曲线表示,可描述各粒径区间段颗粒的含量等信息。
3 结果与讨论
3.1 颗粒轨迹分析

图3为颗粒轨迹计算结果呈现的不同时间步颗粒群状态。由图3可知,颗粒群进入选粉机内部后,共完成了两次分级过程,第一次分级发生在选粉机底部壳体与返料锥之间,即重力分级区。在重力分级区内,粒径较大的颗粒由于受到的气体曳力小于自身重力,不能随气流上升到选粉机转子叶片区域,最后因与壳体碰撞失去动量从粗粉出口排出,粒径较小的颗粒则随气流继续上升。第二次分级发生在转子叶片区域,即离心分级区,完成重力分级后进入离心分级区的颗粒中,粒径较大的颗粒受到转子径向向外的离心力大于向内的气体曳力,被甩向导风叶片和壳体壁面,因与导风叶片或壳体壁面碰撞后失去动量从粗粉出口排出;粒径较小的颗粒受到的离心力小于气体曳力,随气流进入转子内部后,从选粉机细粉出口排出,作为成品被收集。
3.2 细粉颗粒质量流率结果分析
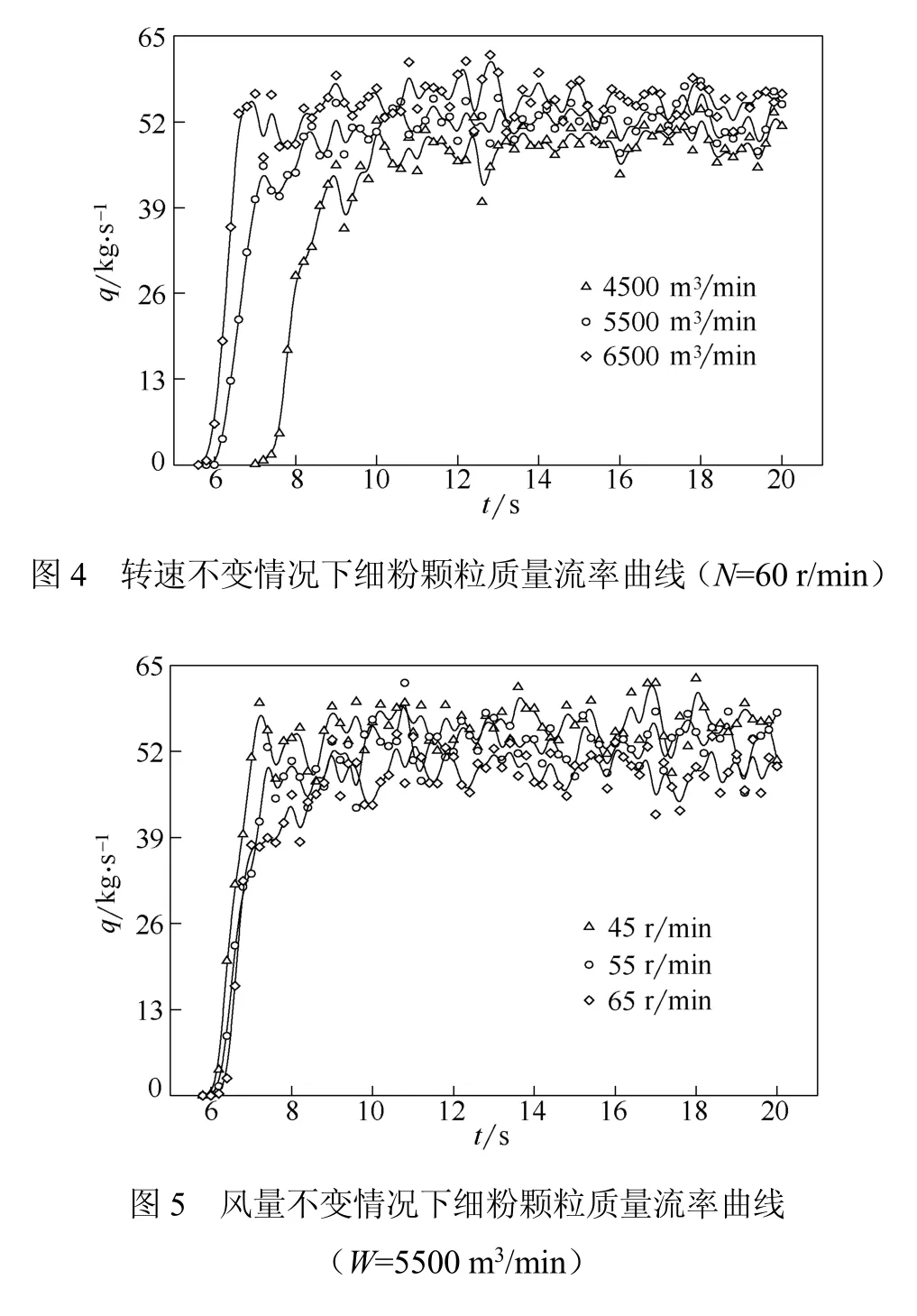
图4和图5为不同工况细粉颗粒质量流率曲线。由图可知,各工况下细粉颗粒质量流率随时间变化可分为两个阶段,线性增长阶段和动态平稳阶段。线性增长阶段可描述为选粉机的流场初始化过程:颗粒从入口进入到分级完成,最后被捕集,在初始化过程中,平面捕集颗粒的质量从无到有,颗粒质量流率不断增大。而动态平稳阶段则描述的是进出口颗粒达到物料平衡时选粉机稳定输出的状态。由图4中曲线对比可知,转速不变,随风量增大,细粉颗粒质量流率增大。由图5中曲线对比可知,风量不变,转速增大,细粉颗粒质量流率减小。在曲线动态平稳阶段取点计算出细粉颗粒质量流率均值,工况1~6分别为47.69 kg/s、51.4 kg/s、52.92 kg/s、54.54 kg/s、52.90 kg/s和 49.78 kg/s。
3.3 粗粉颗粒质量流率结果分析
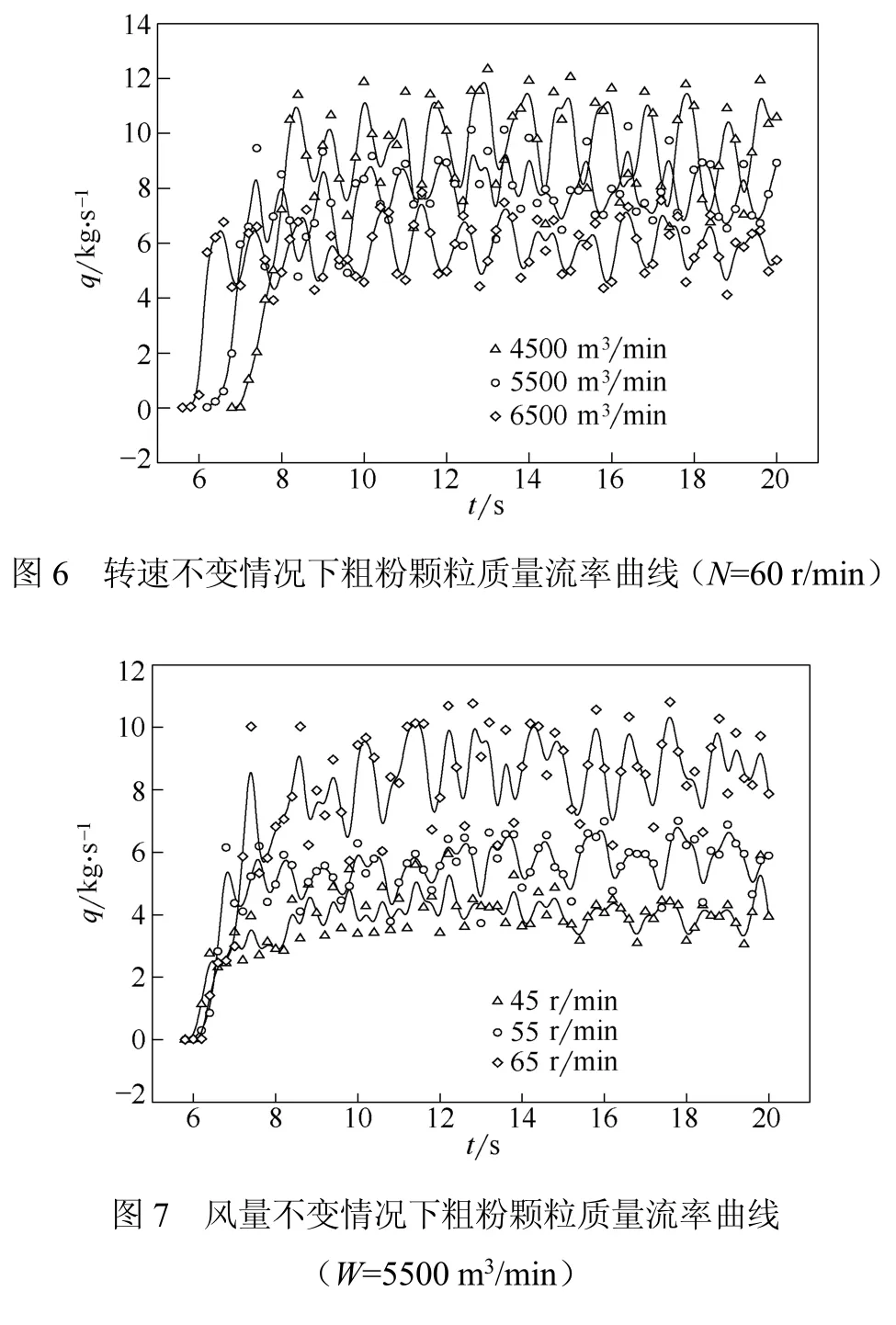
图6和图7分别为不同工况粗粉颗粒质量流率曲线。由图可知,粗粉颗粒质量流率随时间变化也呈现线性增长和动态平稳两个阶段。分别对比图6和图7曲线可知,转速不变,随风量增大,粗粉颗粒质量流率减小;风量不变,转速增大,粗粉颗粒质量流率增大。在曲线动态平稳阶段取点计算出粗粉颗粒质量流率均值,工况1~6分别为12.31 kg/s、8.58 kg/s、7.08 kg/s、5.46 kg/s、7.10 kg/s和10.22 kg/s。
3.4 细粉颗粒粒径分布结果分析
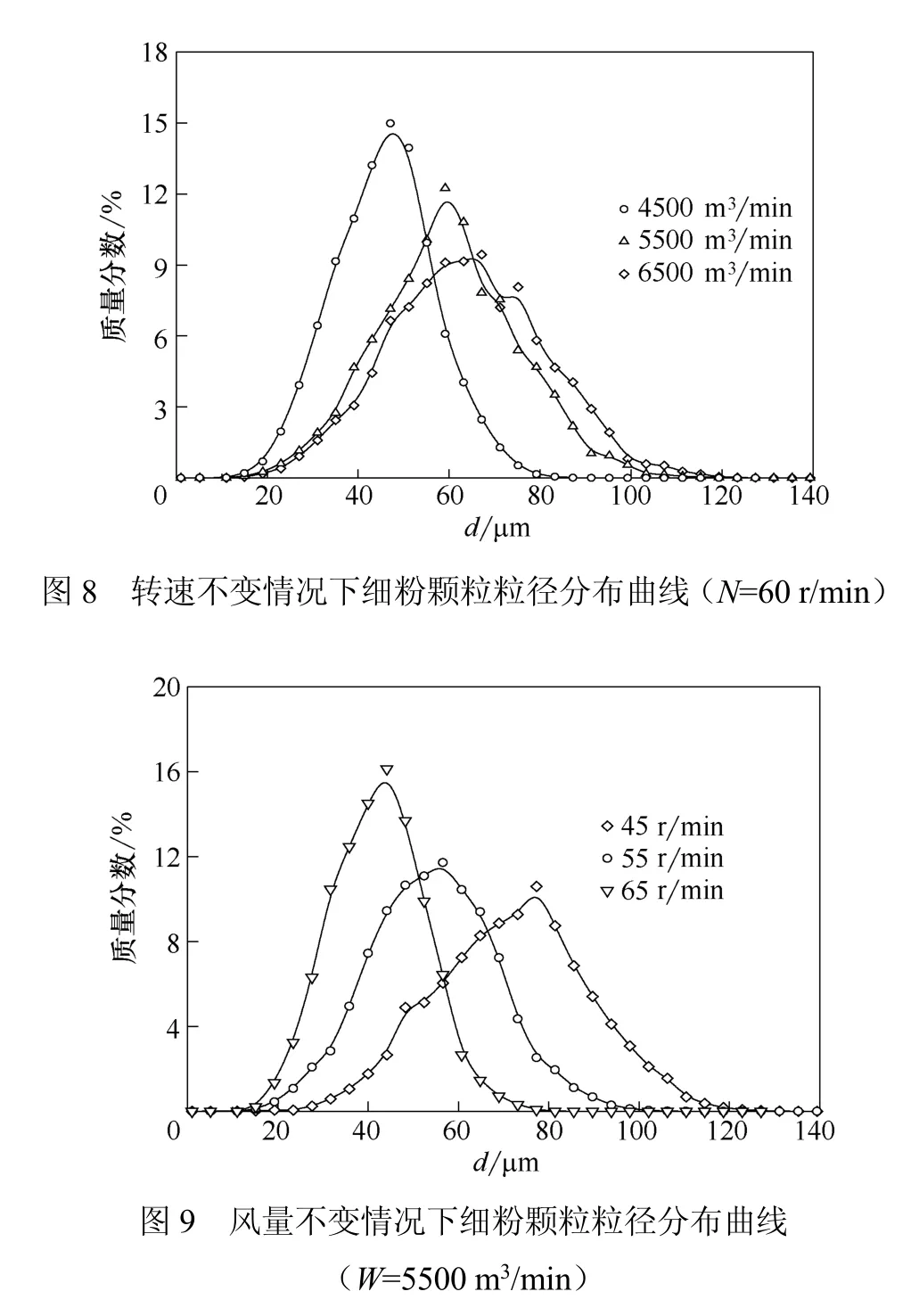
图8和图9为不同工况下选粉机细粉颗粒粒径分布曲线。由图可知,各工况下细粉颗粒粒径分布曲线近似正态分布,分布曲线普遍规律为,粒径较小(<10 μm)和较大(>100 μm)的颗粒含量都较低,中间粒径(30~60 μm)的颗粒含量较高。由图8和图9曲线对比可知,转速不变,随风量增大,粒径分布曲线变宽,且曲线极大值右移;风量不变,随转速增大,粒径分布曲线变窄,且曲线极大值左移。
4 模拟与实验对比分析
4.1 细粉颗粒质量流率实验对比分析
利用实验对颗粒轨迹追踪模拟方法得到的细粉颗粒质量流率结果进行实验对比分析。取工况点5参数进行分级实验,在相同物理模型的选粉机分级实验中,风量为5500 m3/min,转速为55 r/min,喂料量为60 kg/s。选粉机稳定输出后,监测细粉颗粒质量流率为49.85 kg/s,运用(模拟值-实验值)/模拟值×100%计算出细粉颗粒质量流率模拟结果与实验值的相对误差为6.12%。
4.2 细粉颗粒粒径分布实验对比分析
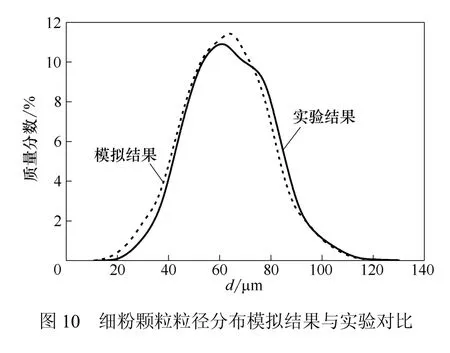
对实验中工况5参数下选粉机细粉颗粒采集样品进行粒度分析,绘制了粒径分布曲线,并与模拟结果进行比较,如图10。由图10可知,模拟结果与实验结果粒径分布曲线在走势和相关点数值都比较吻合。根据计算,两曲线<30 μm颗粒含量相对误差为8.26%,30~100 μm颗粒含量相对误差为9.37%,大于100 μm颗粒含量相对误差为6.54%。
5 结论
(1)应用计算流体动力学(CFD)理论,运用DPM模型的颗粒运动方程对时间积分求解了颗粒运动轨迹,结果表明:颗粒在选粉机内共完成两次分级,重力分级和离心分级。对二维平面离散颗粒的捕集和采样结果进行处理,考察了稳定阶段细粉和粗粉的质量流率并研究了不同工况下细粉颗粒粒径分布情况。
(2)模拟与实验对比分析结果表明:细粉颗粒质量流率模拟结果与实验结果误差为6.12%,细粉颗粒粒径分布模拟曲线与实验曲线较吻合,其中小于30 μm颗粒含量相对误差为8.26%,30~100 μm颗粒含量相对误差为9.37%,大于100 μm颗粒含量相对误差为6.54%。
(3)研究结果为分析和预测选粉机不同工况下的成品产量和粒径分布提供了模拟方法,也为分析选粉机分级效率与分级精度性能技术指标、最佳工况参数调试奠定了研究基础。
符号说明
d——颗粒粒径,m
颗粒组的平均粒径,m——
N——选粉机转速,r/min
n——颗粒组的分布指数
Qn——第n个时间步细粉出口颗粒质量,kg
Qn+1——第n+1个时间步细粉出口颗粒质量,kg
q——单位时间内细粉出口颗粒质量,kg/s
t——时间,s
Δt——非稳态时间步长,s
u——气流速度,m/s
up——颗粒速度,m/s
W——选粉机风量,m3/min
x——坐标轴x方向
Yd——大于某粒径的颗粒质量加权含量,%
τp——颗粒松弛时间,s下角标
n——时间步序列,1,2,3
[1]刘建寿,赵红霞.水泥生产粉碎过程设备[M].武汉:武汉理工大学出版社,2005:211-218.
[2]Roland N.CFS-HD:A new classifier for fine classification with high efficiency[J].International Journal of Mineral Processing,1996,44-45:723-731.
[3]Roland N.Fine classification with vaned rotors:At the outer edge of the vanes or in the interior vane free area[J].International Journal of Mineral Processing,2004,74:S137-S145.
[4]Guo Lijie,Liu Jiaxiang,Liu Shengzhao,et al.Velocity measurements and flow field characteristic analyses in a turbo air classifier[J].Particle Technology,2007,178(1):10-16.
[5]Finch JA.Modeling a fish-hook in hydro cyclone selectivity curves[J].Powder Technology,1983,36(1):127-129.
[6]Nageswararao K.A critical analysis of the fish hook effect in hydro cyclone classifiers[J].Chemical Engineering Journal,2000,80(1-3):251-256.
[7]刘家祥,何廷树,夏靖波.涡流空气分级机内湍流涡频谱对其性能的影响[J].北京化工大学学报,2003,30(5):48-51.
[8]黎国华,聂文平.涡轮分级机内腔流场的数值仿真研究[J].武汉理工大学学报,2004,26(5):71-73.
[9]杨庆良,刘家祥.涡流空气分级机内流场分析与转笼结构改进[J].化学工程,2010,38(1):79-83.
[10]黄强,于源,刘家祥.涡流分级机转笼结构改进及内部流场数值模拟[J].化工学报,2011,62(5):1264-1268.
[11]杜妍辰,王树林.颗粒在涡轮式分级机分级轮中的运动轨迹[J].化工学报,2005,56(5):823-828.
[12]Xu N,Li G H,Huang Z C.Numerical simulation of particle motion in turbo classifier[J].China Particuology,2005,3(5):275-278.
[13]高利苹,于源,刘家祥.涡流空气分级机转笼转速对其分级精度的影响[J].化工学报,2012,63(4):1056-1062.
[14]黄强.涡流空气分级机转笼及导风叶片结构改进的研究[D].北京:北京化工大学,2011:44-48.
[15]Fluent Inc.Fluent user’s guide[M].Pennsylvania:Fluent Inc.,2003:97-102.
[16]赵啦啦,刘初升,闫俊霞,等.颗粒分层过程三维离散元法模拟研[J].物理学报,2010,59(3):1870-1876.
[17]张德胜,施卫东,张华,等.不同湍流模型在轴流泵性能预测中的应用[J].农业工程学报,2012,28(1):66-72.
[18]郑钢镖,康天合,柴肇云,等.运用Rosin-Rammler分布函数研究煤尘粒径分布规律[J].太原理工大学学报,2006,37(3):317-319.
[19]王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2004:124-125.
[20]Pope S B.Turbulent Flows[M].Cambridge:Cambridge University Press,2000:463-557.
