风车安装船的站立稳定性数值分析
2013-10-09张永康李英杰庄建军
张永康,李英杰,王 匀,倪 涛,庄建军
(1.东南大学机械工程学院,江苏南京211189;2.江苏大学机械工程学院,江苏镇江212013;3.南通中远船务工程有限公司,江苏南通226005)
随着能源紧缺状况的加剧和风电场土地资源的日益紧张,海上风能发电成为可再生能源的发展新方向,风车安装船是海上风电领域的核心技术.风车安装船通过桩腿与海床地基的相互作用为海洋作业和风电机组安装提供一个平稳的工作平台.风车安装船处在复杂多变的海洋自然环境中,受到风、海浪、海流及海冰形成的载荷作用,其桩腿站立稳定性直接影响到船的作业性能和安全.风车安装船通过桩腿来实现其站立,桩腿承受竖向和横向的载荷,因此,考虑桩土相互作用,分析风车安装船的稳定性是必须考虑的问题.
本研究以南通中远船务有限公司风车安装船为例,对风车安装船在2种不同地基模型下进行力学特性分析,并对比2种地基模型下的分析结果,以证明考虑桩土相互作用对风车安装船的设计和稳定性校核的必要性.
1 海洋环境载荷计算
1.1 风载荷计算
风速的设计应根据平台的作业地区和作业方式确定.《海上移动平台入级与建造规范》[1]规定风压p按照下式计算:

式中:v为设计风速,m·s-1.
作用于构件上的风力F应按下式计算,并确定其合力作用点的垂直高度,即

式中:p为风压,Pa;S为平台在平浮或者倾斜状态时,受风构件的正投影面积,m2;Ch为暴露在风中构件的高度系数,其值可根据构件高度选取;Cs为暴露在风中构件的形状系数,其值可根据构件形状选取,也可根据风洞试验决定.
1.2 波浪和海流载荷计算
风车安装船的波浪设计标准,要考虑到工况时的最不利情况,以保证船体的安全,波浪选取以波流耦合力最大时相对应的相位角.海流计算时取流向与波浪相位角相同.波浪载荷和海流载荷根据莫里森公式[2]获得:
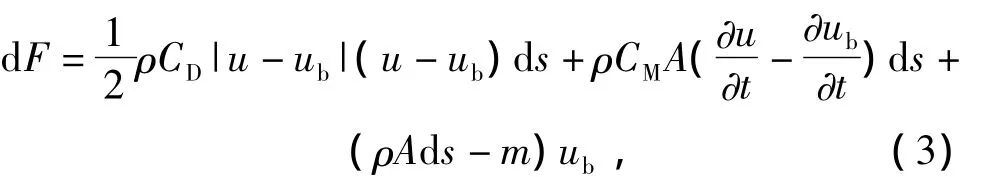
式中:ρ为海水密度;u为结构元件增量微元段的运动速度;ub为相应的加速度;m为微元段的质量;CD为柱体的拖曳力系数,CD=0.6~1.0;CM为柱体的惯性力系数,CM=1.3~2.0;s为海水深度;A为桩腿截面积.
2 有限元模型建立
2.1 风车安装船基本参数
该风车安装船为带有6个圆壳形桩腿自航自升式船体,可在4.8m浪高和14 m·s-1的风速下完成海上风电机组的高精度吊装;最大载质量6 000 t,船体质量为20 000 t,单根桩腿提升能力3 750 t.桩腿尺寸:外径5.01 m,壁厚1.09 m,桩腿长71 m.材料参数:弹性模量2.1×1011Pa,泊松比0.3,密度7 800 kg·m-3.环境参数:水深40 m,风速14 m·s-1,波高4.8 m,波周期8 s,海面流速1.7 m·s-1.
2.2 桩腿的有限元模型
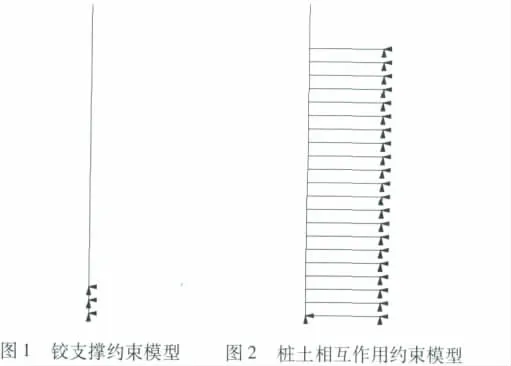
桩腿结构性能的稳定直接影响到船体是否能够正常作业,且桩腿部分与不同介质接触,因此有限元模型建立十分困难.本研究桩腿为圆壳形结构,泥线以上采用PIPE59单元,泥线以下采用PIPE16三维单元.为比对,根据2种模型建立约束条件:传统铰支撑模型,按照规定[1],建立泥面以下3 m处铰支承约束模型(图1);建立桩土相互作用约束模型(Winkler地基模型),入泥深度假设为20 m(图2).
2.3 桩腿的非线性分析
一般情况下,位于浅水的导管架平台由于自身刚度大,自振频率高,不用进行动力分析.但是本研究风车安装船由于桩腿具有大直径、超长的特点,桩的自由站立长度达到40m以上[3],导致桩的长径比很大.由于桩腿柔性相对较大,长期受海洋波流动荷载作用,可能产生较大动位移和动应力,且在外载荷作用下,结构发生屈曲之前会产生较大变形,从而引起结构的非线性响应.因此,为确保风装船安全可靠,有必要考虑结构大变形的非线性动力分析.求解非线性问题的有限元方法可分为增量法、迭代法和混合法.根据风车安装船结构特点,为减少误差,结构的动力非线性求解采用混合法.
3 传统的铰支模型分析
3.1 波浪相位角的搜索
作用在海洋结构物上的波浪力的计算是结构设计中最关键、最困难的,如采用STOKES五阶波理论时,相位角φ的取值对于作用于结构的波浪载荷值影响较大.进行结构静力分析时,是以最大波浪力加载到船体上,以此来校核船体稳定性,因此,进行静力分析前,需要对相位角φ从0°~360°进行搜索,以找到波流耦合力最大时的相位角.本算例中,波浪载荷、浮力载荷、海流载荷都在ANSYS的water table中给予设定,风载荷以分布载荷的形式通过ANSYS的定义载荷功能施加在结构物上.设置环境载荷参数时,将波浪相位角处留空.利用ANSYS的APDL命令流功能搜索相位角,建立波流耦合力-相位角曲线(见图3),得出当波流耦合力最大时,相对应的相位角为112°.
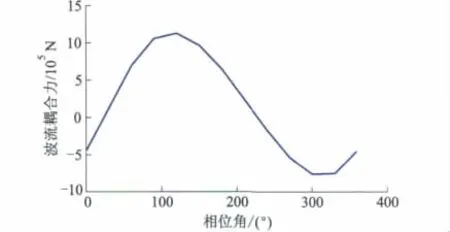
图3 波流耦合力-相位角关系曲线
3.2 结果分析
桩腿载荷施加:横向载荷(垂直于桩腿轴线方向),根据文献[4]取波浪力入射角为0°,且取波浪相位角为112°时的波浪耦合力,风载方向与波浪力方向一致;垂向载荷(平行于桩腿轴线方向),取单桩最大提升力.设置相应边界条件对风车安装船桩腿进行分析.
3.2.1 静力分析
根据安装船基本参数,可估算在风、浪、流载荷作用下,桩腿贯入泥土深度为3 m,在海水中深度为40 m,海面以上高度为28 m,并以最低端为固定约束,采用ANSYS对桩腿进行静力学分析.得出桩腿结构最大位移为0.006 83 m,发生的位置位于桩腿顶部,在固桩端出现最大弯矩3.66×107N·m、最大应力10.9 MPa、应变值6.76×10-3m.
3.2.2 结构模态分析
桩腿模态分析主要是获得桩腿的自然频率、振型以及振型参数等,可以使得桩腿结构设计避免共振或者以特定的频率进行振动,其分析结果还可以作为桩腿瞬态动力分析的基础[5].本研究中风车安装船桩腿属于超大型且对称的特点,采用适用于大型对称特征值求解问题的分块兰索斯法进行求解.桩腿前五阶模态振型如图4所示,结构固有频率依次为0.82,4.72,12.7,23.2 和35.8 Hz.

图4 桩腿前五阶模态振型
3.2.3 瞬态动力分析
波浪力是一种随时间变化的载荷,对桩腿的动力影响不可忽略,有可能产生较大动位移和动应力,用Full方法进行瞬态动力分析,其中瑞利阻尼系数为α和β,α和β与常用的黏性比例阻尼系数ξ关系如下:

式中:f为频率.
根据式(4)和式(5)及模态分析得到的前两阶固有频率,由于结构的频率范围在0.6~10.0之间,所以 ξ=0.03,得 α =0.041 7,β=0.010 83.对桩腿结构的瞬态动力求解得出桩腿最大位移7×10-2m大于桩腿静力分析时最大位移6.83×10-3m,但差距不大,此时桩腿最大应力为10.9 MPa,远低于桩腿材料屈服强度,说明本桩腿结构刚度很大,足以在最不利工况载荷下平稳作业.
4 桩土相互作用模型的分析
国内外学者[6-11]采用桩靴与地基相互作用模型对海洋平台进行了研究,然而本风车安装船的桩腿超长,柔性大,易发生大变形、大位移,有必要建立桩腿和土壤间的相互作用模型,应用Winkler地基模型[5],采用 COMBIN39单元,选取p-y曲线法来计算桩腿和土壤间相互作用,以泥线至桩底20 m深土壤作为弹簧单元分层,针对每个深度对应土层,每1米建立一个COMBIN39单元.通过将不同深度下p-y曲线数输入到ANSYS中的D-F实常数设置中来定义COMBIN39单元.土对桩腿的作用简化为侧向弹簧,在距桩腿轴线3 m处(图2右侧)的泥面以下部分,沿与轴线平行的方向建立21个节点,将这些节点分别与其水平对应的桩腿节点连接创建Elements,并将其依次定义为COMBIN39单元.桩端约束为固定约束,计算模型如图2所示.风车安装船桩腿插入泥土深度为20 m,海面上高度为11 m,以实测p-y数据作为土壤参数.
5 2种模型计算结果对比分析
静力对比分析结果如表1所示.表1中桩土相互作用模型的静力参数都比铰支模型的大,位移大87.4%,弯矩大 35.2%,应力大 11.0%,应变大10.7%.充分说明采用铰支模型对风车安装船稳定性的分析偏于安全,无法正确反映风车安装船稳定的状况,过高估计桩腿的安全性,而考虑桩土相互作用的模型用来研究风车安装船的稳定性更为合理.

表1 静力分析对比结果
铰支模型和桩土相互作用模型的最大弯矩都发生在了桩端处,而没有出现在水面附近,这是由于本研究中风车安装船的直径和壁厚很大,使用的是超高强度钢,且桩腿建造工艺是整条桩腿一次切割而成,所以整体强度很高,不易屈服变形,为风车安装船平稳作业提供安全保障.模态分析对比结果如表2所示.

表2 模态分析对比结果
由表2可知:桩土相互作用模型1阶频率小于铰支模型,而高于1阶的频率又比铰支模型大.我国各海域波浪平均周期为3~7 s,最大周期为13.7 s,可见,桩腿激振频率小于1 Hz.因此,主要考虑桩腿1阶模态,桩土相互作用考虑了土对桩腿的影响,弹簧约束增加了桩腿弹性支撑,约束时弹性约束刚度减少,柔度增加,致使其振动频率较小.但减小幅度不是太大,这是由于桩腿整体刚度很大,振幅较小,导致桩腿周围土的弹性约束不是太明显.高于1阶频率又比铰支模型大,这是由于桩腿周围的弹性约束自身的范围有限.随着振动频率的增大,弹性约束可视为刚性固定约束,导致其频率较高于铰支模型.
6 结论
超大型风车安装船对稳定安装作业的要求更高,因此,对风车安装船进行非线性动力学分析是必要的.桩土相互作用对风车安装船站立稳定性有显著的影响.研究表明:有限元边界条件对桩腿结构强度稳定性分析影响较大,桩脚处铰支约束模型的计算分析结果相对保守,而弹性支撑更接近实际.本研究为风车安装船稳定性研究提供了一种分析手段.
References)
[1] 中国船级社.海上移动平台入级与建造规范[S].北京:人民交通出版社,2005.
[2] 杨树耕,藤明清,孟昭瑛,等.有限元分析软件ANSYS在海洋工程中的应用(续1)[J].中国海洋平台,2000,15(5):40-46.Yang Shugeng,Teng Mingqing,Meng Shaoying,et al.The finite elementanalysis software ANSYS's application in ocean engineering [J].China Offshore Platform,2000,15(5):40-46.(in Chinese)
[3] 刘 润,闫澍旺,毛永华,等.海洋工程中桩身自由站立稳定性影响因素分析[J].海洋工程,2006,24(3):6-13.Liu Run,Yan Shuwang,Mao Yonghua,et al.Study on influence factors for pile stick-up stability in ocean engineering[J].The Ocean Engineering,2006,24(3):6-13.(in Chinese)
[4] 李 虎,吴卫国,甘 进.考虑结构桩土相互作用自升式作业平台研究[J].华中科技大学学报:城市科学版,2010,27(3):86-90.Li Hu,Wu Weiguo,Gan Jin.Research on multi-purpose offshore jack-up platform based on ANASYS[J].J of HUST:Urban Science Edition,2010,27(3):86-90.(in Chinese)
[5] 杨 进,刘书杰,姜 伟,等.ANSYS在海洋石油工程中应用[M].北京:石油工业出版社,2010.
[6] 李 强.基于桩-土相互作用的自升式平台桩靴强度研究[D].大连理工大学船舶工程学院,2008.
[7] Kellezi L,Stromann H.FEM analysis of jack-up spudcan penetration for multi-layered critical soil conditions[C]∥International Conference on Foundations.Lyngby,Denmark:GEO,2003:411-420.
[8] Kellezi L,Hofstede H W L,Hansen P B.Jack-up footing penetration and fixity analyses[C]∥The Proceedings of the First International Symposium on Frontiers in Offshore Geotechnics.Perth,Australia:Taylor and Francis/Balkema,2005:559-565.
[9] Kellezi L,Denver H,Kudsk G,et al.FE skirted footings analyses for combined loads and layered soil profile[C]∥The14th European Conf on Soil Mech and Geotechnical Eng,2007:341-346.
[10] Kellezi L,Kudsk G,Hofstede H.Skirted footings capacity for combined loads and layered soil conditions[C]∥The BGA International Conference on Foundations.Dundee,Scotland:IHS BRE Press,2008:24-27.
[11] Zhang Youhu,Bienen Britta,Cassidy Mark J,et al.The undrained bearing capacity of a spudcan foundation under combined loading in soft clay[J].Marine Structures,2011,24(4):459-477.
