松花江流域水环境BOD-DO模拟及参数分析

李 平，马 放

(哈尔滨工业大学城市水资源与水环境国家重点实验室，黑龙江哈尔滨150090)

河流水质模拟在进行流域污染控制、水环境规划、水质预测及评价中发挥着重要的作用，为污染物总量控制和水功能区水质目标环境管理提供了有效的理论支撑［1-2］.水质模拟过程是利用水体历史数据、污染物的物理化学演变规律，建立相应的数学、物理、化学及试验模型描述水体中污染物质与河流水质之间的响应关系，对河流水环境系统行为进行模拟、预测和评价，是水环境监督管理的重要工具［3-4］.河流水质模拟中模型各项参数(生化耗氧速率、大气复氧速率、生化耗氧量的沉淀和悬浮系数、氮化合物的硝化速率等)的测定和估计是建立水质模型的重要工作前提和基础，模型参数是否精确直接关系水质模拟能否真实反应污染实际过程［5-6］.

为了进一步准确模拟、预测和评价松花江流域河流水环境系统行为，本研究利用O'Connor水质模型建立松花江河段BOD-DO之间的响应关系，为进一步开展流域水环境水质模拟研究和松花江流域水环境保护及污染物总量优化分配奠定基础.

1 材料与方法

1.1 河段水文概况

松花江佳木斯段全长201 km，流经佳木斯、桦川、绥滨、富锦、同江等市县，并与黑龙江汇合于同江市.松花江下游地处三江平原，河道宽，分叉较多.历史上径流量年变化幅度较大，存在明显的丰、枯周期.枯水年与丰水年径流量比为差异较大，年内径流量极不平衡，一年四季存在丰、平、枯3个水期.丰、枯期流量相差百倍以上.试验江段为松花江下游佳木斯-富锦江段，长167 km，河道弯曲系数1.17.

1.2 罗丹明B示踪及水团追踪试验

罗丹明B示踪试验:淡水、河水、海水中弥散仅从理论上来分析比较困难，采用现场示踪试验，选用易溶于水、稀溶液呈强荧光的工业染料碱性罗丹明B为示踪剂，采用荧光分光光度法进行测定，确定纵向弥散系数，研究干流扩散规律.示踪剂罗丹明B(分析纯)瞬时投放，在河流的下游布置断面采样，样品送回化验室检测，波长578 nm定量，水质指标采用国家标准方法［7］测定.

水团追踪试验:利用人工投放的方式在河道中造成一个含有机物的污水团，进行水团跟踪监测，利用水团质量浓度沿程衰变情况，来推定河流对污染物质的降解规律.BOD(20)为现场测定，冰封期、明水期在佳木斯江段前后共进行15次水团追踪作业.冰封期水温为0℃，以初始投加为第1天计，共监测14 d，各断面监测时刻如下:佳木斯下1∶00，桦川6∶00，新城14∶30，富锦18∶00;明水期为14 ℃，以初始投加为第1天计，各断面监测时刻如下:佳木斯下8∶00，桦川19∶00，新城8∶00，富锦400.表1列出了15次实测数据.

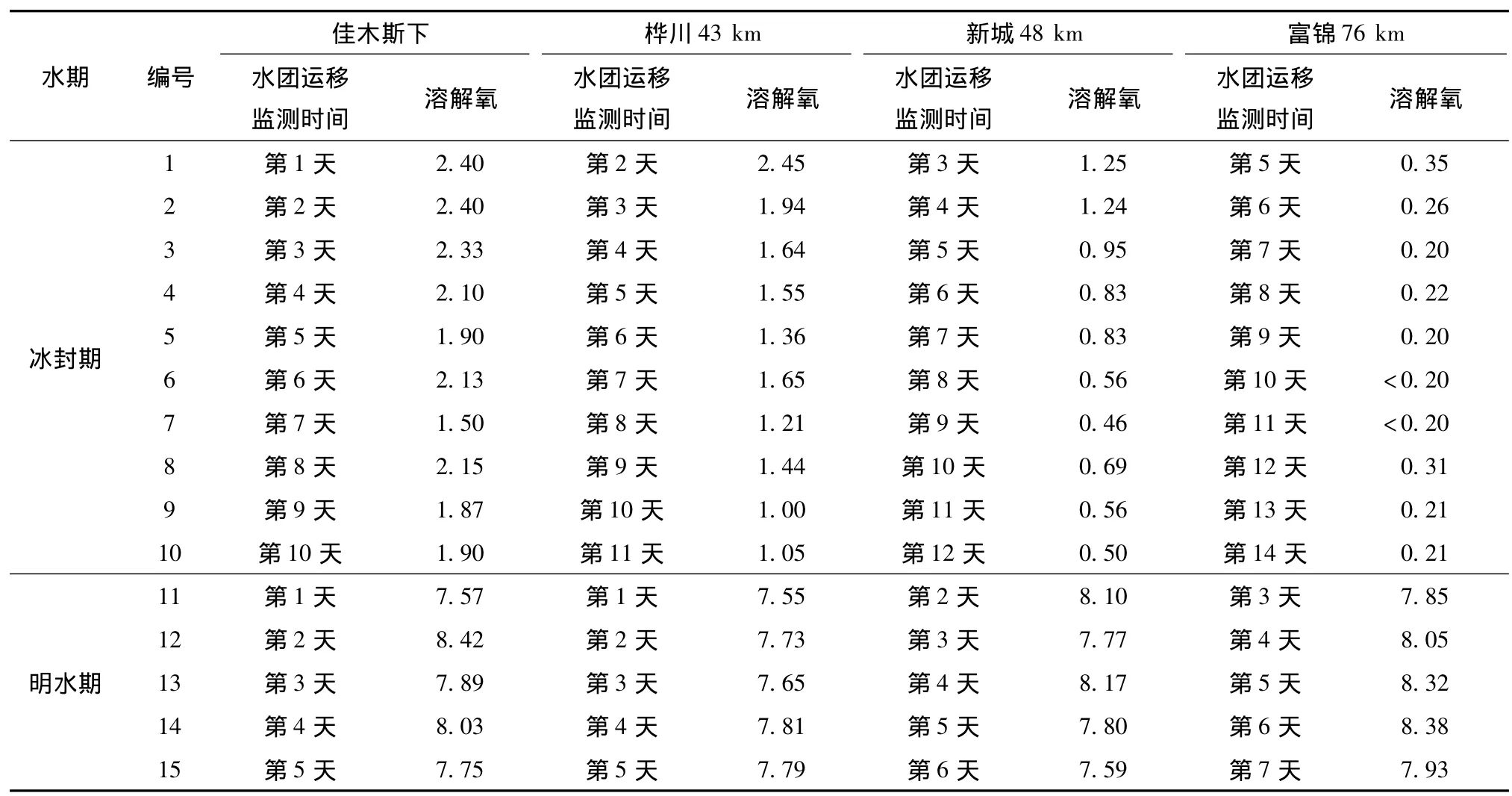
表1 松花江佳木斯江段水团追踪数据表 mg·L-1

2 结果与分析

2.1 BOD-DO模型选择及改进

污染物在河流水动力的作用下发生稀释、扩散、沉降、降解等过程.根据河流的水文特点、污染物性质建立BOD-DO模型，来描述水体中污染物随时间和空间迁移转化规律的数学方程［8］，对这一过程进行预测.溶解氧质量浓度是衡量现有水质与水体能否保证水生物系统良性循环的重要标志.因此建立溶解氧模型描述河流水质状态，进而建立排污量与水质状态的定量关系，则可将河流纳污能力与污染排放，用模型的模拟解来表示，构成水环境容量的定量计算方法［9-10］.取6月松花江佳木斯某段水样，检测其20 d的BOD质量浓度变化过程，如图1所示.

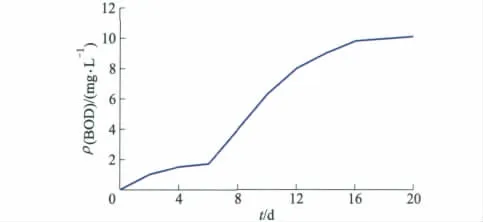
图1 松花江佳木斯段20 d的BOD变化过程

由图1可知:该段BOD质量浓度存在2个明显阶段变化，即CBOD降解和NBOD降解，显示松花江该段存在着硝化过程，且硝化过程较为超前，故而选择同时考虑CBOD和NBOD的衰减与耗氧作用的O'Connor模型进行松花江佳木斯江段BOD-DO模拟.基本方程如下:

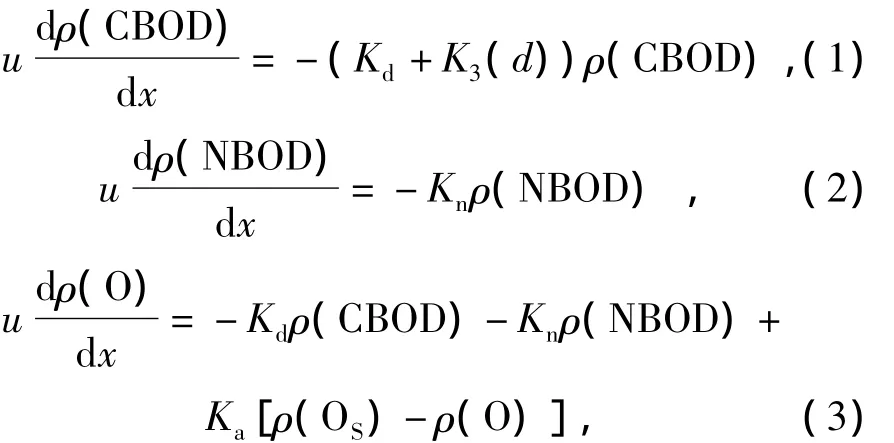
式中:ρ(CBOD)为河水质量浓度，mg·L-1;ρ(NBOD)为河水 NBOD 质量浓度，mg·L-1;ρ(O)为河水DO质量浓度，mg·L-1;ρ(Os)为河水t℃时饱和溶解氧质量浓度，mg·L-1;x为距排污口河水流动距离，m;u为河水流速，m·s-1;Kd为CBOD衰减系数，d-1;Ka为河水复氧系数，d-1;K3(d)为CBOD沉浮系数，d-1;Kn为NBOD衰减系数，d-1.

但O'Connor基本模型并未将CBOD，NBOD的物理沉浮作用表达清楚，综合Thomas，引入K3表征悬浮作用的CBOD物理变化和O'Connor的CBOD总衰减率的改进方法，改进O'Connor模型，以对松花江佳木斯江段BOD-DO进行精确模拟:

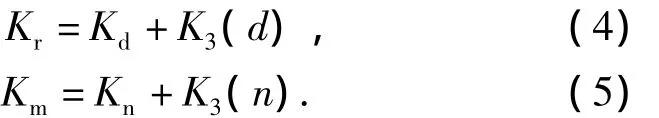
则式(1)变为

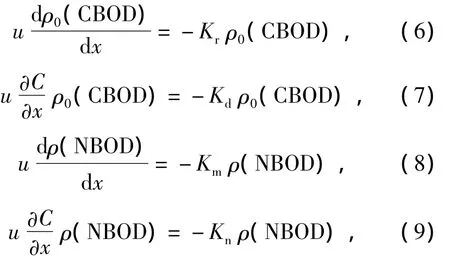
式中:Kr为CBOD总衰减速率，d-1;Km为NBOD总衰减速率，d-1;K3(n)为NBOD物理沉浮系数，d-1.

CBOD方程解为

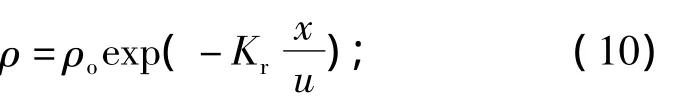
NBOD方程解为

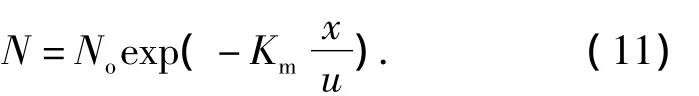
则假定为一维无离散，溶解氧方程变为式(12).为方便式(12)求解，令，根据常数变易法，可求出式(12)解析解，即溶解氧方程为(13).公式如下所示:

式中:ρo(CBOD)为初始断面河水CBOD质量浓度，mg·L-1;ρo(NBOD)为初始断面河水NBOD质量浓度，mg·L-1;ρo(OO)为初始断面溶解氧质量浓度，mg·L-1;t'为任意断面时间.由式(10)-(13)构成改进O'Connor模型解析解.松花江佳木斯段溶解氧模型由以上方程组建立.

2.2 BOD-DO模型的参数识别分析

2.2.1 模型参数的识别

复氧系数Ka对于河流溶解氧质量浓度变化影响较大，国内一般均以采用经验公式估值最普遍，但由于时空限制，模拟精度较差，不同公式估值相差较大，另外利用示踪剂实测Ka，因价格昂贵，适用范围窄，很难广泛采用.CBOD的衰减系数Kd、NBOD衰减系数Kn识别是通过利用BOD的20 d过程线进行试验室模拟，完成相应参数识别.根据松花江佳木斯下游断面BOD的20 d实测过程数据，采用最小二乘法既可确定目标Kd和Kn，其中Kn一般在0.1～0.3 d-1.结合试验前期资料获得了耗氧系数常数Kd(20℃)=0.250 d-1，Kn(20℃)=0.172 d-1，简化了松花江佳木斯段水质模型参数Ka，Kr和Km识别过程，可以实现利用水团追踪试验中溶解氧实测数据结合多维参数的最优化估值法识别Ka，Kr和Km.

多维参数最优基本方法是从给定的初始参数值Ki出发，每次增减一定的量，逐步改善目标函数J(K)，直到其满足目标值收敛的误差要求.研究采用梯度搜索法，在起点的目标函数值J(Ki)下降速率最快的方向(一阶负梯度方向)，按定步长进行搜索，每次改进目标函数值，得到新的起点，反复迭代计算，直到满足要求.目标函数取溶解氧的模型计算值与实测值之差的平方和为

用梯度搜索法寻出最优解.

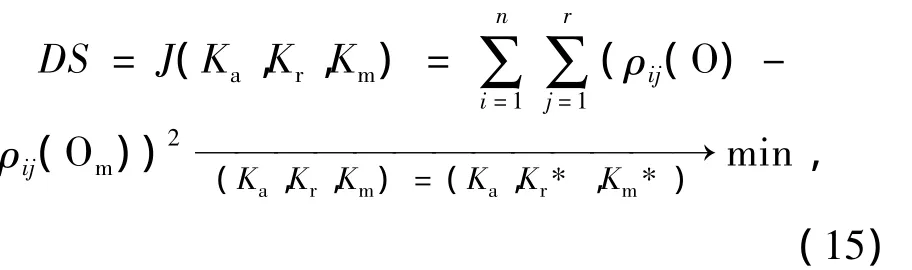
式中:ρij(O)为模型计算的第i次监测第j个断面的河水溶解氧质量浓度，mg·L-1;ρij(Om)为实测得到的第i次监测第j断面的河水溶解氧质量浓度，mg·L-1.

改进的O'Connor模型参数估值采用最优搜索计算框图［11-12］，参数识别分冰封期和明水期分别进行，获得15组实测数据，10组用于识别，5组用于参数验证.1-10号为冰封期实测数据选择1-7号数进行参数识别，8-10号数据进行参数验证;11-15号为明水期实测数据选择11，13和14号数据进行参数识别，12和15号数据进行参数验证.利用表1水团追踪数据以及Kd=0.250 d-1，Kn=0.172 d-1输入值推求冰封期和明水期的Ka，Kr，Km值，相应参数识别结果如表2所示.

表2 参数识别结果 d-1

分别将冰封期、明水期参数识别值取平均值，作为冰封期和明水期参数优选值，如表3所示.

表3 冰封期和明水期参数值 d-1

2.2.2 模型参数的温度修正

模型参数修正方程基本型式为

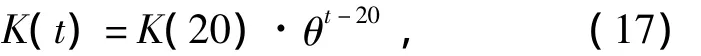
式中:θ为温度修正系数，一般介于1.047～1.140之间;K(t)为任意温度t时的参数;K(20)为20℃时的参数.根据表3的参数识别结果，确定相应温度修正系数，进行温度修正，可得松花江佳木斯段溶解氧模型参数修正方程如下:Kd=0.25×1.047t-20;Kn=0.172×1.088t-20;Kr=0.833×1.011t-20;Km=0.651×1.025t-20;Ka=0.87×1.024t-20.

2.2.3 模型参数的验证

分别利用冰封期8-10号数和明水期12，15号数据进行参数验证.验证结果如表4所示.

表4验证结果可以表明，分不同水期识别并验证得到的模型参数值，在精度方面可以满足水质模拟的要求，利用改进的模型推求得模拟计算值与实测值的相对误差，除两点由于实际溶解氧ρ(DO)较低而偏大外，分别为14.79%，50.69%，其余均在10%之内.15个模拟计算值与实测值的相对误差平均在10%以下，所确定的模型参数应用在研究松花江佳木斯段水质模拟中较为合适.

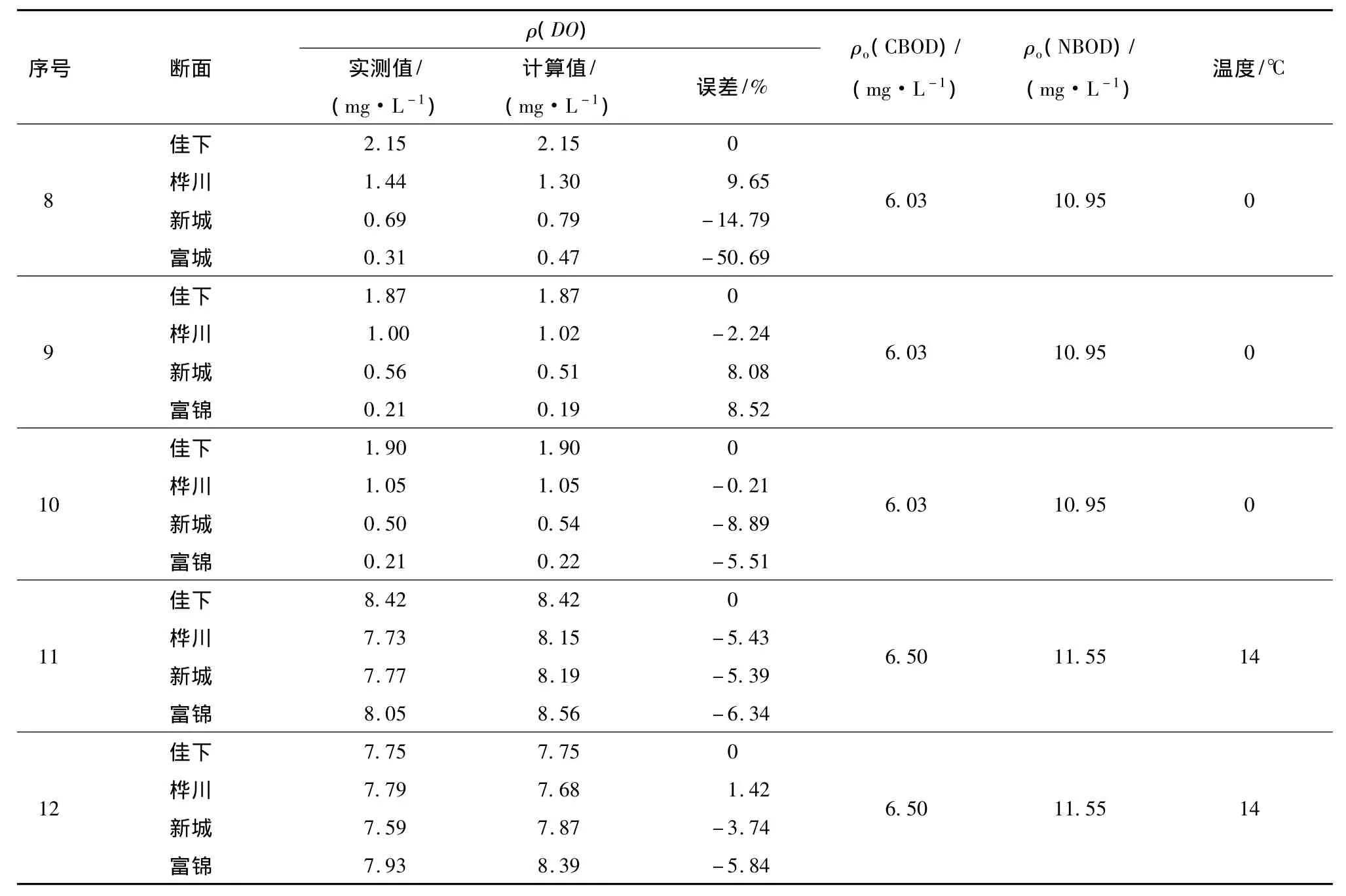
表4 松花江溶解氧模型验证结果

2.3 参数灵敏度分析

对改进O'Connor模型溶解氧有关的各项参数进行灵敏度分析.检验的方式是保持其他参数不变，即只改变被检验参数，令模型中Kd，Kn，Ka，Kr，Km等各项参数分别增减幅度10%，ρo(CBOD)=6.50 mg·L-1，ρo(NBOD)=11.55 mg·L-1，ρo(O)=8.00 mg·L-1，由模型输出12∶00和24∶00两个断面时刻DO变化幅度考察其灵敏性，结果如图2所示.

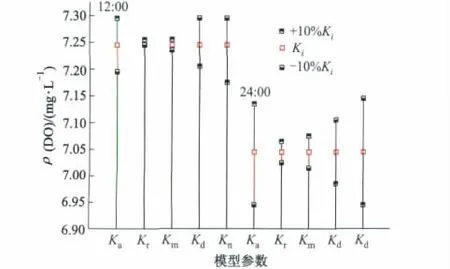
图2 模型参数灵敏度分析

由图2模型参数变化分析可以判定模型对应灵敏程度，松花江佳木斯段改进的O'Connor溶解氧模型中，大气复氧系数Ka和Kn变化所引起的DO变化幅度最大，CBOD耗氧系数Kd次之，BOD总衰减速率Km和Kr灵敏度最低.

3 结论

1)应用改进的O'Connor溶解模型研究松花江佳木斯段BOD-DO变化关系，水团追踪试验验证了模型耗氧系数、复氧系数及总衰减系数等重要参数取值的合理性，其精密可以满足水质模拟的要求.

2)对松花江佳木斯段BOD-DO模型参数进行了任意温度下的参数修正，Kd=0.25×1.047t-20，Kn=0.172 ×1.088t-20，Kr=0.833 ×1.011t-20，Km=0.651×1.025t-20，Ka=0.87×1.024t-20.

3)对模型预测结果影响较大的参数为大气复氧系数Ka和Kn，CBOD耗氧系数Kd次之，BOD总衰减速率Km和Kr灵敏度最低.

References)

［1］ Sullivan A B，Jager H I，Myers R.Modeling white sturgeon movement in a reservoir:the effect of water quality and sturgeon density ［J］.Ecological Modelling，2003(167):97-114.

［2］ Madsen H.Parameter estimation in distributed hydrological catchment modelling using automatic calibration with multiple objectives［J］.Advances in Water Resources，2003，26:205-216.

［3］ 刘 伟，刘洪超，徐海岩.基于MIKE11模型计算河流水功能区纳污能力方法［J］.东北水利水电，2009(8):69-72.Liu Wei，Liu Hongchao，Xu Haiyan.Calculation method of water environment capacity for water function area based on MIKE 11model［J］.Water Resources＆Hydropower of Northeast China，2009(8):69-72.(in Chinese)

［4］ 金春久，王 超，范晓娜，等.松花江干流水质模型在流域水资源保护管理中的应用［J］.水利学报，2010，41(1):86-92.Jin Chunjiu，Wang Chao，Fan Xiaona，et al.Application of water quality model to the river basin water resources protection and management for the mainstream of the Songhua River［J］.Journal of Hydraulic Engineering，2010，41(1):86-92.(in Chinese)

［5］ 张永祥，蒋 源，施同平，等.基于WASP 7.2河流水质模型的应用研究［J］.北京水务，2010(1):22-24.Zhang Yongxiang，Jiang Yuan，Shi Tongping，et al.Study on the application of model about river water quality［J］.Beijing Water，2010(1):22-24.(in Chinese)

［6］ 宋新山，邓 伟.环境数学模型［M］.北京:科学出版社，2004.

［7］ 国家环境保护总局.水和废水监测分析方法［M］.4版.北京:中国环境科学出版社，2002.

［8］ McAvoy D C，Masscheleyn P，Peng C，et al.Risk assessment approach for untreated wastewater using the QUAL2E water quality model［J］.Chemosphere，2003(52):55-66.

［9］ 李 兰，李志永，刘金才.BOD5-DO参数反问题偶合模型的研究［J］.水科学进展，2000，11(3):255-259.Li Lan，Li Zhiyong，Liu Jincai.A BOD5-DO parameter inverse coincidence model［J］.Advances in Water Science，2000，11(3):255-259.(in Chinese)

［10］ 杜彦良，褚君达.河流连续点源的垂向混合规律研究及其应用［J］.环境科学学报，2000，20(6):699-703.Du Yanliang，Chu Junda.Study on verticalmixing law of continuous point source in nature river and its application ［J］.ACTA Scientiae Circumstantiae，2000，20(6):699-703.(in Chinese)

［11］ 芮孝芳.河流水文学［M］.南京:河海大学出版社，2003:143-156.

［12］ 马常仁，徐得潜，周 慧，等.基于最小二乘法与最速下降法的综合衰减系数的率定［J］.水利科技与经济，2012，18(1):20-24.Ma Changren，Xu Deqian，Zhou Hui，et al.Rating at synthetic attenuation coefficient based on least-square method and the steepest descent method ［J］.Water Conservancy Science and Technology and Economy，2012，18(1):20-24.(in Chinese)