桁架结构可靠性优化设计的微分演化算法

胡长远，唐和生，2，薛松涛，3，邓立新

(1.同济大学结构工程与防灾研究所，上海200092;2.同济大学土木工程防灾国家重点实验室，上海200092;3.东北理工大学建筑学科，日本仙台982-8577)

不确定性普遍存在于结构使用和施工中的各个阶段，因此结构分析中应该采用不确定性的力学模型才更为合理［1］.处理不确定性的方法有多种，其中，当不确定变量的概率分布是已知时，基于概率可靠性的方法是最好的分析方法.在工程结构系统可靠性优化设计中，通常是将可靠度指标显示化处理作为优化的约束条件，将之转化为确定性的优化问题，再与某种优化算法相结合来进行求解［2］.R.V.Grandhi等［3］提出两点近似法构造极限状态函数，且把外层优化的目标函数和可靠度约束分别用样条函数近似.

近年来，应用智能优化算法对结构系统进行可靠性优化设计取得了不少成果，例如，文献［4］系统地讨论了采用遗传算法，在框架结构静、动力下，基于单元与体系可靠度的尺寸与形状优化设计中的应用.作为一种新颖的算法，自从R.Storn和K.Price 1996年引入了微分演化(differential evolution，DE)算法之后，该方法在解决复杂的优化问题上得到了很多关注［5］.微分演化算法新颖的特征使其具有更好鲁棒性和更快收敛速度.该算法已被广泛应用于工程优化、可靠度分析、主动控制及识别问题［6-9］.

本研究以桁架结构为对象，考虑结构物理参数、几何尺寸和作用载荷的不确定性，进行结构有限元和可靠性分析，在此基础上，构建桁架结构基于可靠度约束的优化设计模型，运用微分演化算法进行形状优化设计.

1 桁架结构可靠性优化微分演化算法

1.1 基于可靠度的桁架结构可靠性优化模型

针对结构优化中的最一般情况，构建以结构构件尺寸和节点坐标为设计变量，以结构重量均值极小化为目标函数，同时具有位移和应力性态约束的结构优化设计数学模型.考虑结构物理参数、几何尺寸和作用载荷的不确定性，从而导致结构的位移和应力等性态约束均成为随机变量函数，它们以概率(可靠度)形式列出.至此，基于可靠性的结构优化模型为

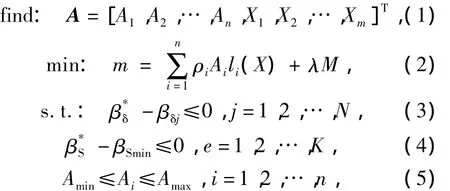
式中:A是设计向量;A1，A2，…，An为杆件截面积;X1，X2，…，Xm为变量连接后各节点的坐标;Ai，ρi和li是分别第i类设计变量的截面面积、密度和杆件长度;m是结构质量;βδj为结构中第j个自由度的位移可靠性指标;βSmin为结构中第e个单元的应力可靠性指标的最小值;β*δ，β*S分别为设计给定的可靠指标;Amax，Amin分别为设计变量的上下限，n为截面面积变量数;X¯c，Xc分别为第c坐标的上下限，m为节点变量数;N为位移约束的数目;K为结构中单元的数目;M为预先定义的一个足够大的正数;λ为罚函数因子，当结构设计变量满足约束条件时，λ=0，否则λ=1.针对以上优化问题，本研究采用DE算法进行求解.

这里首先对概率约束进行等价显式处理［4］.模型中所有概率约束均可表示为

式中:P*为设计给定的可靠度;R表示结构某物理量(位移或应力)的许用值;S表示在结构荷载作用下与R对应的响应值(位移或应力)，在一般情况下R与S两者是彼此独立的.由可靠性分析的一次二阶矩法，式(7)可被表示为

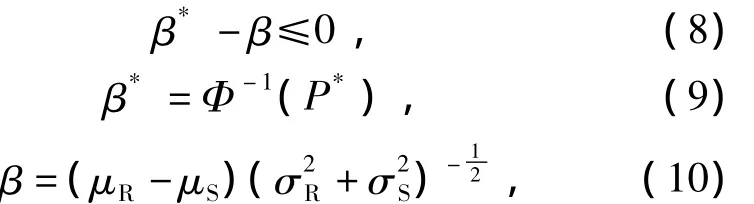
式中:β*为给定的可靠指标;β为可靠性指标;Φ-1(·)表示标准正态变量分布的反函数;μ，σ分别表示随机变量的均值和标准差.

1.2 微分演化算法

一个包括t个参数的优化问题可以用一个t维的向量来描述，该向量可以表示为:xi=(xi1，xi2，…，xit)T∈S，i=1，2，3，…，NP.其中 S∈Rn为优化问题的搜索空间;DE算法利用NP作为向量xi1每一代的个体数.类似于遗传算法，DE算法通过变异、交叉和选择过程实现种群的更新进化.

1.2.1 变异过程

变异目的是为了保证种群的多样性，同时用合适的参数变化来指导已有的目标向量在合适的时间内达到一个更好的结果，从而保证了搜索的鲁棒性.变异操作过程中，上一代的个体，i=1，2，…，NP，(其中G表示代数)根据不同的变异方式进行更新则得到第G+1子代向量=本研究采用 R.Storn等［5］推荐的DE/current-to-best/1/bin变异方式进行结构优化，该变异方式为

式中:x(beG

s)t为算法第G代种群中适应值最小的个体;F1和F为变异常数，均为非负实数，其大小控制了变量间的差异，保证进化的进行;r1，r2为互不相同的整数，分别从集合{1，2，…，i-1，i+1…，NP}中随机选出向量编号.

1.2.2 交叉过程

与GA算法相似，DE算法中个体经过变异后也进行交叉操作.对于群体中第G+1代经过变异过程后的向量个体v(iG+1)按照

进行交叉，将产生新的个体，即

式中:j=1，2，…，t;rand(j)∈［0，1］，是t个0 ～1 之间相互独立的随机数中的第j个;randn(i)是随机从集合{1，2，…，t}中取得个体向量维度的序号;CR为交叉因子，将决定个体之间交叉的概率.

1.2.3 选择过程

DE算法采用和GA算法不同的贪婪准则:通过比较由变异和交叉产生的子代个体和父代个体，选择适应值好的变量，即如果父代个体适应度值更优将继续保留在种群中;否则保留子代个体.选择过程如下:

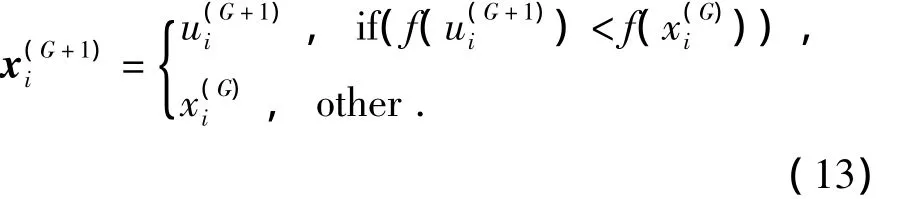
1.3 桁架结构可靠性优化的DE算法流程

根据前述可靠性分析和所构建的优化设计数学模型，桁架结构可靠性优化设计DE算法的流程如下:

1)初始化DE算法参数，并在设计空间内随机初始化种群，it=0.

2)进行有限元分析，计算出每个个体所代表的设计变量对应的结构形态变量，如各杆应力和节点位移.

3)进行结构可靠性分析得结构响应量的数字特征.

4)判断是否满足包括可靠性约束等约束条件，满足约束条件时λ=0，否则λ=1.

5)计算每个个体的评价函数值.选出最优秀个体xbest.

6)对每个个体进行变异操作，并对每个个体(父代)以及变异个体进行交叉操作，得到新的个体(子代).

7)计算每一个子代个体以及父代个体的适应值;选择适应值好的作为下一代种群中的个体.

8)计算每一个下一代的个体适应值，并找到最优个体;如果新的最优个体适应值比上一代xbest适应值好，则更新xbest，称为当前最优个体.

9)满足算法终止条件，输出最优个体xbest，以及最优个体的适应值，否则返回2).

2 数值分析

为验证本研究所提方法对桁架结构进行优化设计的有效性，以下对一典型的桁架结构(如图1所示)进行可靠性优化设计分析，同时与确定性方法进行比较.

图1为37杆桁架桥的初始形状，节点坐标见表1.

图1 37杆桁架桥

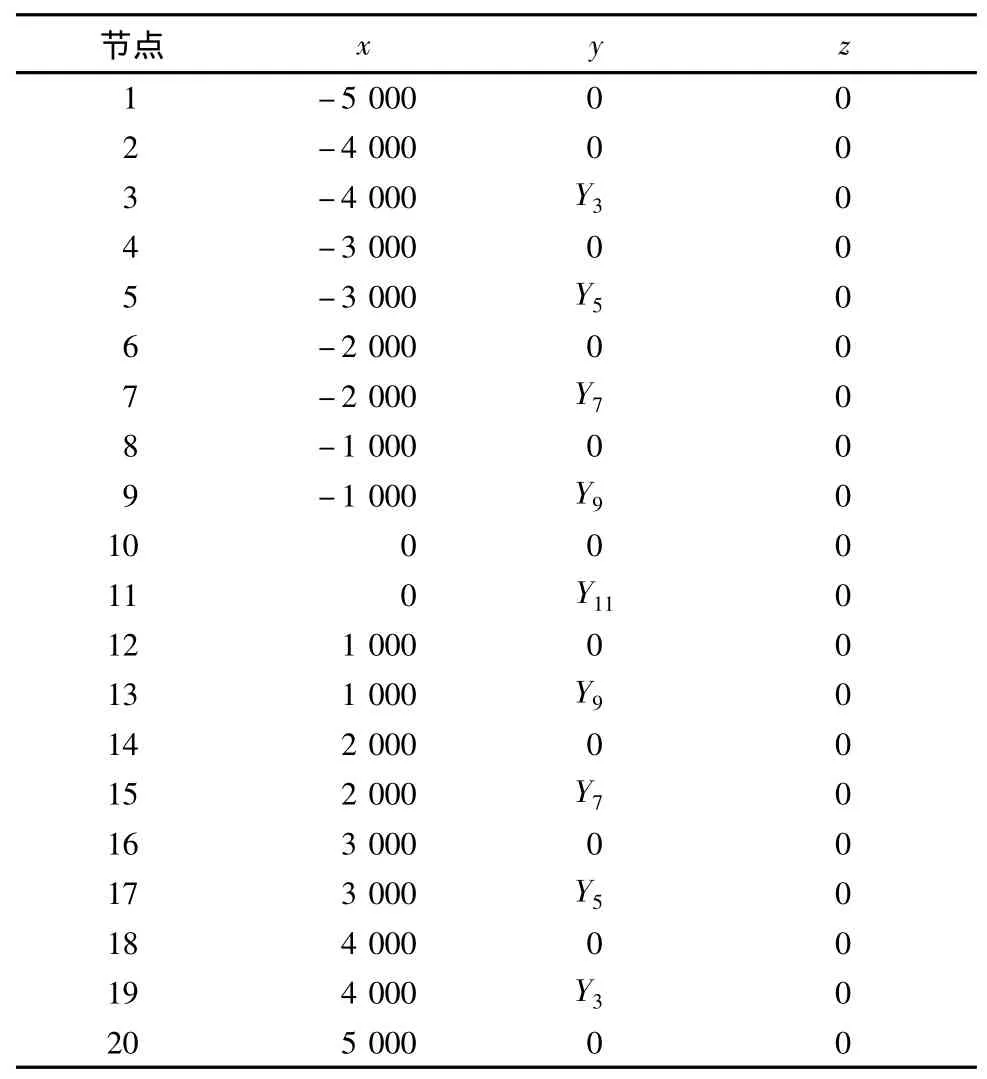
表1 37杆桁架桥节点坐标 mm

假设下弦节点位置保持不变，上弦节点可沿竖直方向移动，结构对称性保持不变，不考虑局部稳定约束.

材料密度为ρ=7 800 kg·m-3，最小截面积为50 mm2.桁架所有杆件采用同一种材料，假设弹性模量E、几何尺寸(杆长)l和外加载荷{P}为不确定随机变量(这里认为3个随机变量为互不相关)，E，l和{P}可分别表示为弹性横量E= ¯E·δE，杆件长度le= η(e)·l和外加荷载{P}= Δp·{P0}，其中 ¯E，η(e)和{P0}为确定性量，是其所代表物理量的均值，三者的值分别为210 GPa，1 000(1 414.2)mm 和 10 kN;δE，l和 Δp为随机因子，三者均值均为1，方差(变异系数)分别为 γ2，γ2和Elγp2.其中 γE，γl和 γp分别为弹性横量、杆件长度和外加荷载的变异系数.

根据结构对称性，取设计变量为［A1，A2，A3，A4，A5，A6A7，A8A9，A10，A11，A12，A13，A14，A15，A16，A17，A18，A19，Y3，Y5，Y7，Y9，Y11］T.DE 算法的参数选择如下:种群大小NP=100;变异因子F=0.6;杂交概率CR=0.85;最大迭代次数Gmax取值500.

利用随机因子法和代数综合法可以得到节点位移和单元应力的统计量［4］，位移随机向量均值{μδ}和方差{σ2δ}分别为

式中:{δ}#为结构的常规位移有限元计算值.单元应力的均值{μse}和方差{σ2se}分别为

式中:D为弹性矩阵;B为几何矩阵;T(e)为单元e从局部坐标系到总体坐标系的坐标转换矩阵.

综上，利用式(10)、(14)和(15)可求得位移可靠指标;利用式(10)、(16)和(18)即可求得应力可靠指标.

当可靠度R分别为0.80，0.90和0.99时，随变异系数γ的不同，结构质量如表2所示.

表2 结构质量表

由表2可以看出:当外荷载、弹性模量和杆件长度分别为随机变量时，对结构的影响差不多.同时也可以看出，多个参数为随机变量时，结构的质量要大于单个参数为随机变量时的质量.当可靠度R=0.90时，Case1的形状优化评价函数曲线如图2所示，图3为Case1优化后的形状.

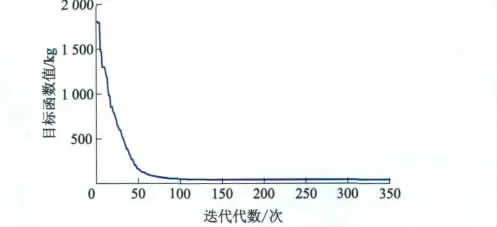
图2 37杆桁架桥形状优化评价函数收敛曲线

图3 37杆桁架桥形状优化结果

由图2可知迭代200次左右时曲线已经收敛.当可靠度R=0.80，变异系数取Case2，Case5和Case8时37杆桁架桥可靠度约束形状最优化结果与确定性方法的优化结果的比较如表3所示.由表3可知:相对于确定性优化的结果，用可靠度考虑不确定性因素后优化结果要偏大，但更接近实际工程.当变异系数不同，可靠度R与桁架总质量的关系如图4所示.由图4可知γ越大或是R要求越高时，桁架结构也越重.

图4 变异系数不同时，可靠度与桁架总质量的关系

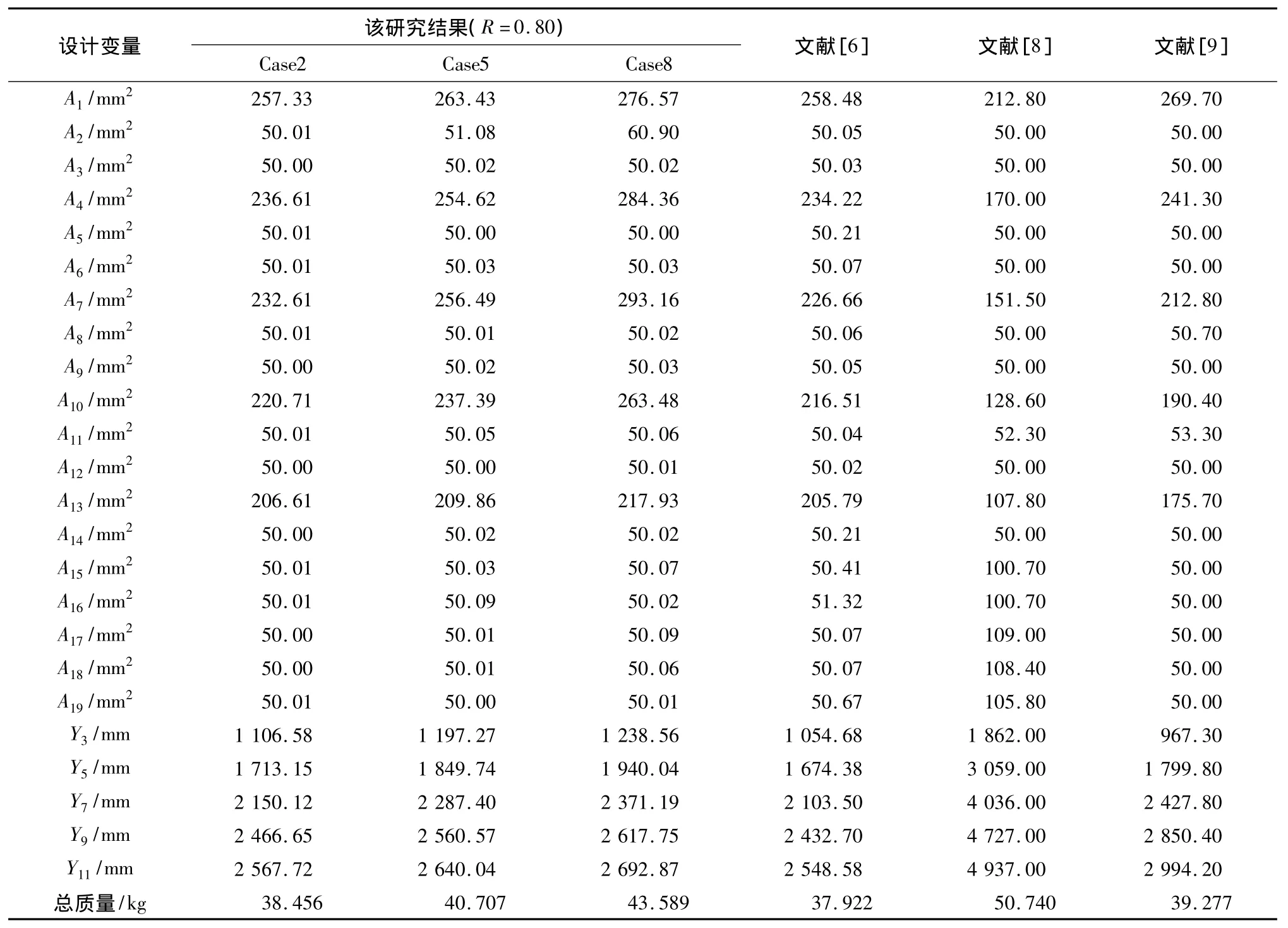
表3 37杆桁架可靠度约束形状最优结果与其他方法比较

3 结论

1)基于可靠度的桁架不确定优化设计的结果比确定性优化的结果偏大，但更加符合工程实际背景.优化结果的大小随着可靠度指标的提高和变异系数的增大而增大.

2)本研究所提出的分析方法能够发挥微分演化算法的优势，计算精度高，运行稳定，可以快速、有效地进行基于可靠度的桁架结构优化设计.

References)

［1］ Hoffman F，Hammunds J.Propagation of uncertainty in risk assessments:the need to distinguish between uncertainty due to lack of knowledge and uncertainty due to variability［J］.Risk Analysis，1994，14(5):707-712.

［2］ Ibrahim R A.Structural dynamics with parameter uncertainties［J］.Applied Mechanics Review，1987，15(3):309-328.

［3］ Grandhi R V，Wang L P.Reliability-based structural optimization using improved two-point adaptive nonlinear appoximations［J］.Finite Elements in Analysis and Design，1998，29(1):35-48.

［4］ 马洪波.随机结构可靠性分析和优化设计研究［D］.西安:西安电子科技大学机电工程学院，2004.

［5］ Storn R，Price K.Differential evolution:a simple and efficient adaptive scheme for global optimization over continuous spaces［J］.Journal of Global Optimization，1997，11(4):341-359.

［6］ 唐和生，王兆亮，薛松涛.微分演化算法在桁架形状优化中的应用［J］.土木建筑与环境工程，2010，32(1):42-50.Tang Hesheng，Wang Zhaoliang，Xue Songtao.The structure shape optimization with differential evolution algorithm［J］.Journal of Civil，Architectural＆Environ-mental Engineering，2010，32(1):42-50.(in Chinese)

［7］ Wang Zhaoliang，Tang Hesheng，Li Pengfei.Optimum design of truss structures based on differential evolution strategy［J］.ICIECS，2009(3):1576-1580.

［8］ 王 栋，张卫红，姜节胜.桁架结构形状与尺寸组合优化［J］. 应用力学学报，2002，19(3):72-76.Wang Dong，Zhang Weihong，Jiang Jiesheng.Combined shape and sizing optimization in truss design［J］.Chinese Journal of Applied Mechanics，2002，19(3):72-76.(in Chinese)

［9］ 王 勇.基于微粒群算法的桁架结构优化设计［D］.上海:同济大学土木工程学院，2008.