最小二乘法在热电偶热电势校准中的应用

赵楠，吴方，刘丹英

(中航工业北京长城计量测试技术研究所，北京 100095)

1 问题的提出

热电偶广泛应用在热处理炉控温和温场测试领域，这些热电偶都需要经过计量部门校准。为了降低校准成本，使用方可以选择几个常用温度点对热电偶进行校准，其他所需温度点的热电动势数值使用多项式曲线拟合法确定[1]，因此最优拟合的阶次就成为研究的重点。本文通过试验数据的比较给出了使用多项式拟合法进行热电偶热电势值计算时的最佳阶次，并对多项式拟合结果进行不确定度评定。

2 多项式拟合结果

依据热电偶检定规程[2－3]，每支热电偶一般只检定3～4个温度点，以廉金属热电偶为例，在已知四个校准点热电势情况下，根据最小二乘法拟合原理，利用Matlab模拟求得一阶多项式拟合、二阶多项式拟合、三阶多项式拟合、四阶多项式拟合、五阶多项式拟合、六阶多项式拟合、七阶多项式拟合的非校准点的实测值与拟合值的差值如表1、表2所示。其中，表1为已知N型热电偶在550，700，830，1000℃热电势情况下，求得690，970，1100℃各阶次多项式拟合中实测值与拟合值的差值;表2为已知K型热电偶400，600，800，900℃热电势情况下，求得300，500，1050℃各阶次多项式拟合中实测值与拟合值的差值。各阶次多项式拟合误差平方和如图1、图2所示。

表1 N型热电偶多项式拟合误差表

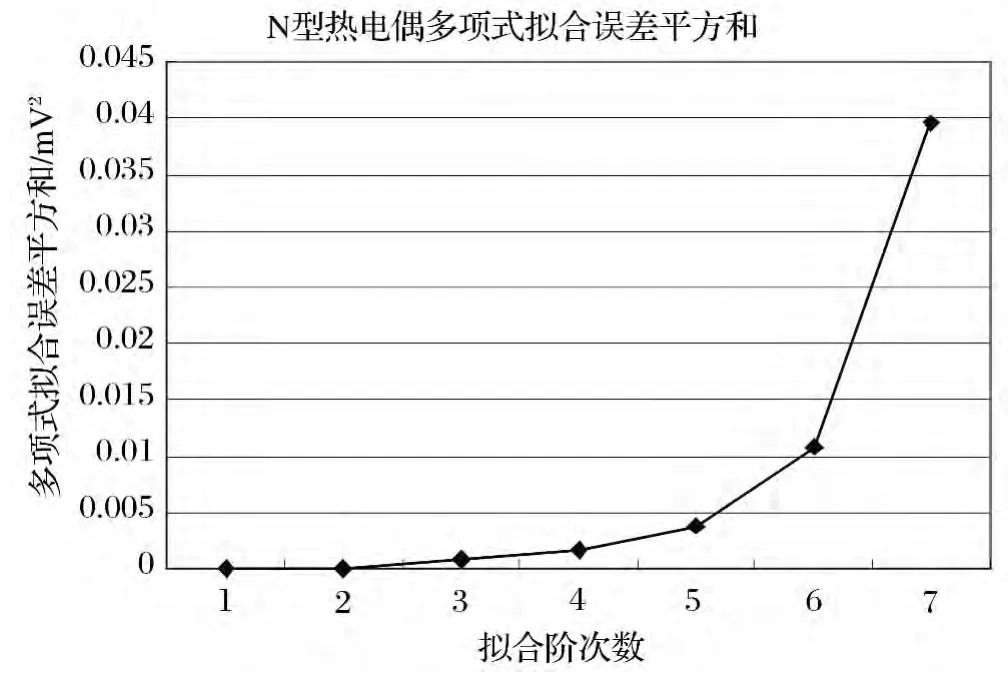
图1 N型热电偶多项式拟合结果分析图

表2 K型热电偶多项式拟合误差表

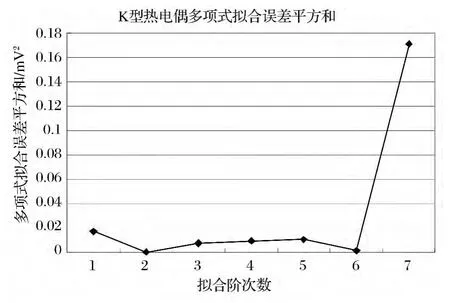
图2 K型热电偶多项式拟合结果分析图

从表1、图1和表2、图2中可以看出:

1)利用多项式拟合曲线时，选择二阶拟合时各测试点拟合误差的平方和最小，为最小二乘拟合的优选阶次[4]。

2)利用多项式拟合曲线，内插温度点拟合结果与实测值差别不大，外推温度点拟合结果与实测值差别相对比较大，使用时应尽量避免使用多项式拟合方法求得外插温度点热电势值。

3)在兼顾降低校准成本和保证实际使用温度点结果可靠的情况下，只需校准使用温度范围的上下限及中间温度点，利用这三个校准点求得二阶拟合曲线，从而求得其他非校准点的方法是可以满足校准需求的。

3 二阶拟合结果的不确定度评定

由于目前对校准结果的表示要求越来越规范，要求每一个校准结果均应有一个不确定度与之相对应，因此需要对非校准点的拟合结果进行不确定度评定。

本文使用热电偶测量温度范围的上下限及中间温度点的校准结果，确定二阶拟合曲线，求得非校准点拟合结果及其不确定度。

假设已知的三个校准点为t1，t2，t3，在这三个分度点上进行校准得到的修正值分别为 Δt1，Δt2，Δt3，而实际需要应用的分度点为t，通过二次多项式拟合得到的修正值为Δt。

所以可得

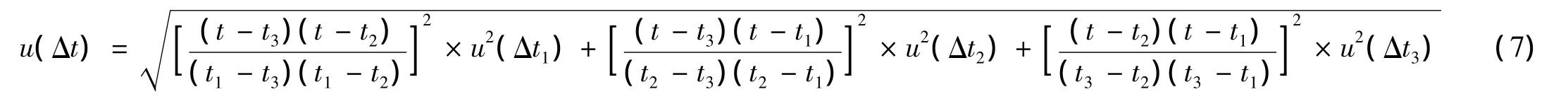
由于u(Δt1)，u(Δt2)，u(Δt3)是已知的校准温度点，的合成标准不确定度，因此可以通过公式 (7)得出该分度点的合成标准不确定度。

4 结论

在热电偶热电势校准时，利用二阶多项式进行最小二乘拟合时拟合精度最高。只需在热电偶使用温度范围的上下限及中间温度点校准，并进行最小二乘拟合从而求得其他非校准点的热电势值，大大降低了校准成本，同时能够保证校准数据可靠。本文同时对这一拟合结果进行了不确定度评定，这对满足国际要求、实现每一个校准结果均应有一个扩展不确定度与之相对应具有一定的理论指导意义和实际应用价值。

[1]王建新，杨世风，隋美丽.Labwindows/CVI测试技术及工程应用[M].北京:化学工业出版社，2006.

[2]国家质量技术监督局.JJG351－1996工作用廉金属热电偶检定规程 [S].北京:中国计量出版社，1996.

[3]国家质量技术监督局.JJG141－2000工作用贵金属热电偶检定规程 [S].北京:中国计量出版社，2000.

[4]赵楠，刘丹英.基于最小二乘法的热电偶特性拟合方法[J].工业计量，2013(2):45－47.

[5]马松龄.最小二乘法在热电偶热电势—温度特性线性化中的应用[J].西安建筑科技大学学报，2001，3(1):86－88.

[6]徐耀松，付华，王丹丹.基于数字采集卡的虚拟测温系统[J].工业控制计算机，2004，17(3):64－65.