印刷电路板设计参数对其翘曲影响的分析
2013-09-28吴许杰牛忠荣程长征
吴许杰, 牛忠荣, 刘 凯, 程长征
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
0 引 言
芯片密度的增加以及功能增强、功率增大是电子工业的发展趋势,从而使得电子元器件逐渐小型化以及I/O输出数逐渐增多,印刷电路板(Printed Circuit Board,简称PCB)上印刷线路的间距以及线路宽度也随之逐渐减小,并且开始更多地采用多层板[1]。多层板中间交叉使用铜线路和各种复合绝缘材料,且PCB工艺温度有时高达250℃以上,由于此时各种材料热膨胀系数的不同,会使PCB发生翘曲。所谓PCB的翘曲是指其与板面垂直方向的位移值,翘曲对于整个封装体有着重要的影响,不仅容易造成连接元器件与PCB之间的焊点发生失效,同时也易使芯片内产生张应力而开裂损坏[2]。
为改善封装的整体可靠性、减小PCB的翘曲和实现对其准确仿真计算,近10年来许多学者做了大量的工作。文献[3]发现铜线路宽度和间距的合理调整可以显著地减小PCB的整体翘曲;文献[4]采用复合材料力学理论建立了PCB翘曲控制的目标函数以及约束条件,对PCB结构进行了优化设计;文献[5]通过将信号层设计图划分为若干区域导入Matlab中,利用Hough变换得到每个区域的有效铜线路方向,在计算均匀化材料特性过程中,考虑了铜线路方向和所占体积比例,从而实现了对PCB仿真计算方法的改进;文献[6]表明有限元分析可以较好地模拟铜电路对PCB整体翘曲的影响,从而可以近似地认为采用有限元模型计算的翘曲值为PCB的真实翘曲值。边界元法在处理薄体结构和占用计算机资源方面有一定优势[7],可以很好地解决热变形和热应力问题[8],一些学者开始尝试将其应用于解决微封装问题中。
翘曲过大会显著地降低电子封装体的安全性,为保障系统的安全工作,从设计阶段开始要对翘曲进行分析控制,而数值模拟则是预测PCB翘曲的有效途径。本文采用有限元法对某PCB的整体结构及力学特性进行模拟仿真,实现了对PCB信号层的真实模拟仿真,并分析了不同约束条件下基板厚度、FR-4材料的弹性模量以及阻焊材料的热膨胀系数对PCB翘曲和应力的影响,从而为PCB设计参数的选择提供一定的参考。
1 PCB结构的力学模型
由于计算机内存资源的有限性以及PCB结构的复杂性,在对PCB进行力学分析时,如果不作合理的简化,则需占用大量的内存资源而难以分析,尤其是分析多层板时。本文分析的某PCB几何尺寸为:58.29mm×38.66mm,总厚度为0.30mm。PCB结构一共4层,其中第1层和第4层均为阻焊层;第2层为基板,采用FR-4材料;第3层为信号层电路,由铜和阻焊材料共同构成。对PCB结构进行力学建模时,忽略了PCB上面的一些次要结构(如过孔等),在不影响其主要物理特征的前提下,简化了分析模型。PCB的各层分布如图1所示。
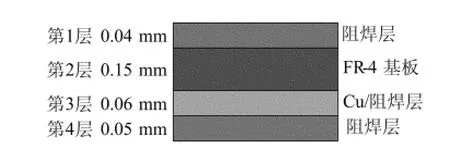
图1 PCB各层分布
PCB使用的材料主要为阻焊材料、金属材料(指铜)和复合材料(FR-4),其中 FR-4材料的泊松比为0.30,其他特性见表1所列,其中,E为弹性模量;α为热膨胀系数。
结构分析中的荷载仅考虑温度荷载,模拟从室温均匀上升到回流焊温度(25~260℃);在25~260℃范围内,铜的热膨胀系数和弹性模量分别为17×10-6K-1和56GPa,其泊松比为0.35;阻焊材料的热膨胀系数和弹性模量分别为60×10-6K-1和3.2GPa,其泊松比为0.30。
PCB结构的约束条件为禁止其刚体位移,模拟其处于自然状态如图2所示,其中,A点为约束X、Y、Z3个方向的位移;B点为约束X、Z方向位移;C点仅约束Z方向位移;X、Y向在板面内,Z向为垂直板面向外的方向。
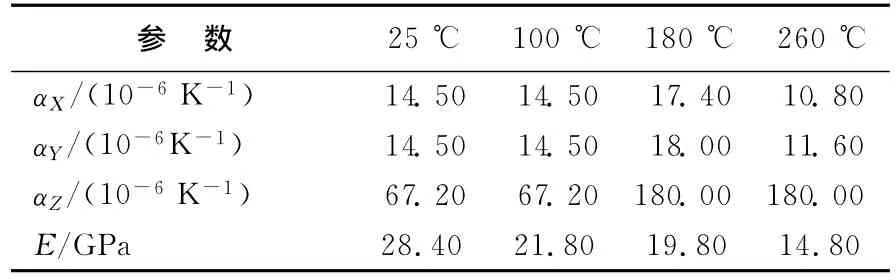
表1 FR-4材料不同温度下的特性

图2 PCB的约束情况
从表1可看出,FR-4材料弹性模量随着温度的变化而变化,ANSYS软件默认相邻两温度之间的弹性模量值是线性变化的(如25~100℃的弹性模量),可根据温度变化选取相应的弹性模量值。
本文采用ANSYS APDL参数化语言对PCB进行建模分析,单元类型选用三维8节点六面体实体单元(solid45),PCB结构的有限元模型共划分为248830个单元和279860个节点。信号层的实际电路图和有限元分析模型对比如图3所示。
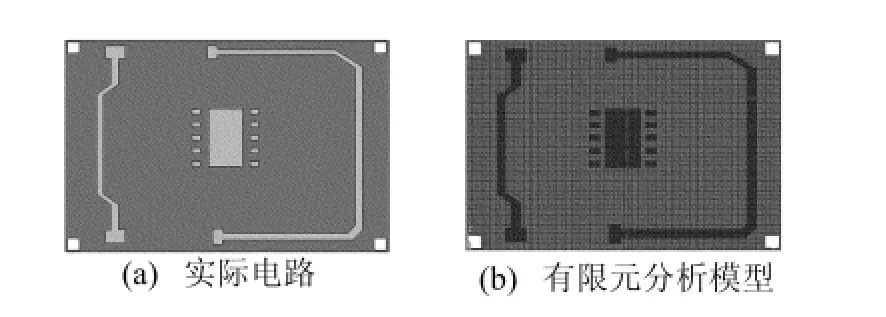
图3 信号层的实际电路图和有限元分析模型
目前许多文献在对PCB进行仿真分析时,只把信号层电路简单地作为1层铜箔或根据构成材料所占体积分数简化为1种材料来处理,这是不符合实际的。对于多层板来说,中间有很多的信号层,它们都是由铜以及一些复合材料构成的,各层含铜的比例不尽相同,铜线路的方向也不是规则统一的,若简单地作为1层铜箔或简化为1种材料来分析,其结果必然与实际状况存在很大的误差。由图3可以发现,本文中PCB结构的有限元模型是按照铜电路的实际分布、走向等划分单元的,并考虑了信号层电路结构所使用的不同材料,反映了PCB信号层的真实状况,另外模型中每层的节点、单元分布均相同,保证了各层间可以严格地实现共节点,从而确保了PCB结构有限元模型的合理性。在对PCB结构进行有限元分析时,共分成了3个设计参数分析组,分别为基板厚度组、弹性模量组和热膨胀系数组,每组选取5个分析实例,分别考察3种设计参数对于PCB翘曲和应力的影响。
2 有限元法计算结果分析
2.1 基板厚度对PCB翘曲的影响
FR-4材料为PCB的重要组成材料,常用作PCB的基材。本文采用有限元法分析FR-4层厚度为0.10、0.15、0.20、0.25、0.30mm 情形下的PCB翘曲及应力值,以探究不同的基板厚度对于PCB翘曲和应力的影响,其他层厚度及分布如图1所示,阻焊材料热膨胀系数为60×10-6K-1。基板厚度组分析得到的PCB最大翘曲值和最大Mises应力结果如图4所示。

图4 基板厚度对PCB翘曲的影响
图4结果显示,随着基板厚度的增加,PCB的最大翘曲值以及最大Mises应力均有所减小,但Mises应力值减小较少。当基板厚度为0.1mm时,PCB翘曲值为9.292mm,当基板厚度为0.3mm时,PCB翘曲值为2.316mm,降低了75.07%;最大 Mises应力值相应地从最高的50.403MPa下降到49.138MPa后几乎保持稳定,仅降低了2.51%。
2.2 FR-4材料的弹性模量对PCB翘曲的影响
FR-4是一种复合材料,种类繁多,不同的FR-4材料的特性是不同的。本文分析了随着FR-4材料弹性模量的变化,PCB的翘曲及应力的变化情况。
基板厚度选取0.15mm,阻焊材料热膨胀系数为60×10-6K-1。第1种FR-4材料的弹性模量见表1所列,第2种材料的弹性模量比第1种材料增加了5GPa(即每个温度下的弹性模量值均增加),第3种材料的弹性模量比第2种材料增加了5GPa,以此类推,共模拟分析了5种不同的FR-4材料,弹性模量组计算得到的最大翘曲和最大Mises应力结果如图5所示(由于FR-4材料的弹性模量随着温度变化而变化,无法直接标出某一值,因此图5中的横坐标用E1~E5代替5种不同FR-4材料的弹性模量)。
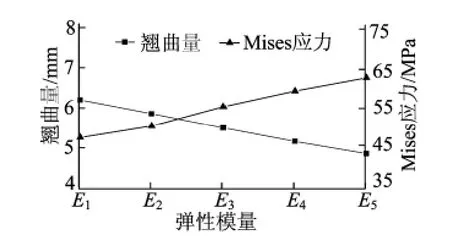
图5 弹性模量对PCB翘曲的影响
由图5可知,当基板厚度为0.15mm时,随着FR-4材料弹性模量的增加,PCB的最大翘曲值有所减小,从第1种FR-4材料的6.234mm下降到第5种材料的4.889mm,降低了21.57%,而最大Mises应力值反而增大了,从最小的49.138MPa 增 加 到 62.980MPa,上 升 了28.17%。
2.3 阻焊材料热膨胀系数对PCB翘曲的影响
PCB翘曲是由于高温下各种材料热膨胀系数的不同造成的,尤其是对于铜和阻焊材料来说,其热膨胀系数相差甚大。
本文研究了降低阻焊材料的热膨胀系数,使其与铜的热膨胀系数逐渐地接近,PCB翘曲值的变化。基板厚度选取0.15mm,热膨胀系数为60×10-6K-1,第2种阻焊材料的热膨胀系数比第1种材料减小10×10-6K-1,第3种阻焊材料的热膨胀系数比第2种材料减小10×10-6K-1,以此类推,共模拟分析了5种不同的阻焊材料。热膨胀系数组仿真计算得到的最大翘曲和最大Mises应力结果如图6所示。
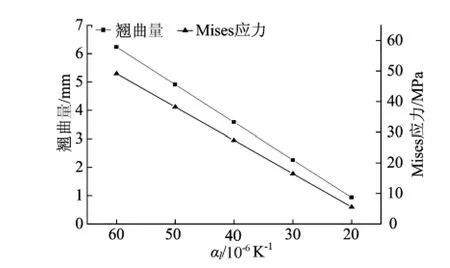
图6 阻焊材料热膨胀系数对PCB翘曲的影响
由图6可看出,当基板厚度为0.15mm时,随着阻焊材料热膨胀系数的减小,PCB的最大翘曲值以及最大Mises应力值均明显地降低了。当阻焊材料热膨胀系数为60×10-6K-1时,PCB翘曲值为6.234mm,当阻焊材料热膨胀系数为20×10-6K-1时,PCB翘曲值为0.935mm,降低了85.00%;最大 Mises应力值从49.138MPa下降到5.550MPa,降低了88.70%。
2.4 不同约束条件下PCB翘曲分析
翘曲度计算公式为:

其中,Q为翘曲度;w为翘曲值;L为PCB结构表面对角线长度。
PCB在温度荷载作用下的翘曲度和应力需满足如下刚度和强度的要求:
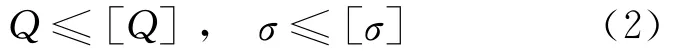
其中,[Q]、[σ]分别为PCB的许用翘曲度和构成材料的许用应力,选用的屈服准则为Mises准则。
根据文献[9]规定,针对表面安装用印制板的弓曲和扭曲应不大于0.75%,其他印制板应不大于1.5%。
目前,电子装配厂许可的翘曲度,无论双面或多层,通常都规定为0.75%,因此本文中许用翘曲度[Q]取值为0.75%。同时,多数FR-4材料的强度为340MPa左右,对该材料可取[σ]为340MPa。
在对PCB结构进行分析时,采用的约束条件为约束PCB的刚体位移,如图2所示。本文考虑PCB在装配状态下的约束条件,即增加4个方孔局部位置垂直板面的位移约束,考察此时PCB的翘曲值和应力值的变化情况。把PCB处于自然状态作为工况1;改变约束条件为装配状态,增加4个方孔局部位置垂直板面的位移约束,PCB结构有限元模型的其他条件保持不变,作为工况2,此时PCB结构在2种工况下的部分有限元计算结果见表2所列。

表2 工况1与工况2的有限元分析结果
表2中,h0为基板厚度;E0为FR-4材料的弹性模量;α0为阻焊材料的热膨胀系数。由表2可看出,增加约束后,PCB的翘曲度明显地减小了,而应力值却相应地增大了。同时有限元分析结果表明,PCB的最大应力位置为4个方孔处FR-4层与信号层的交界位置,具体应力云图如图7所示,图7中未显示出应力较小的阻焊层。
图7表明,在PCB不同层之间的交界处容易发生应力集中现象,在PCB的结构设计和实际生产中应予以重视。
由表2可知,在工况2下,当h0=0.30mm、E0=E1、α0=60×10-6K-1时,此时PCB的翘曲度已经超过许用翘曲度0.75%,而最大应力小于许用应力340MPa,因此通过增加基板厚度可在一定程度上减小翘曲和最大应力;当h0=0.15mm、E0=E5、α0=60×10-6K-1时,此时PCB的翘曲度和最大应力均超出了许用范围,表明在实际应用中,通过增大弹性模量值来减小翘曲的效果未必好;当h0=0.15mm、E0=E1、α0=20×10-6K-1时,其翘曲度和最大应力均在许用范围内。经计算,当h0=0.15mm、E0=E1时,阻焊材料热膨胀系数不大于28×10-6K-1时,均能使PCB满足强度和刚度的要求。有限元分析结果显示,降低阻焊材料的热膨胀系数可以使PCB的翘曲度和应力同时满足刚度和强度要求。

图7 PCB结构Mises应力图
2.5 计算结果分析和设计参数选择
综合以上的计算结果可知,PCB处于自然状态下,通过增大基板厚度可以减小其翘曲和最大应力值,最终分别降低了75.07%和2.51%;增加FR-4材料的弹性模量可以减小翘曲,最终降低了21.57%,但却增加了最大应力值,最终上升了28.17%;减小阻焊材料的热膨胀系数不仅可以很好地减小PCB的翘曲,还可显著地减小最大应力值,最终分别降低了85.00%和88.70%。由此可见,通过减小阻焊材料的热膨胀系数,使其接近铜的热膨胀系数,是控制PCB翘曲的最佳途径。
自然状态下,当基板的厚度为0.10mm时,PCB翘曲值为各组计算结果中最大的;当阻焊材料的热膨胀系数最接近铜的热膨胀系数时,PCB翘曲值为各组计算结果中最小的。最大翘曲与最小翘曲的Z向位移云图如图8所示。图8显示,PCB最大翘曲均发生在PCB的最中间区域。
增大基板的厚度和FR-4材料的弹性模量均相当于增加了PCB的整体刚度,因此可以减小PCB的翘曲。当不断减小阻焊材料的热膨胀系数时,其热膨胀系数不断地接近铜的热膨胀系数,此时在高温下各层的热膨胀值相近,从而可以很好地减小PCB的弓曲和扭曲,因此可以显著地降低翘曲和最大应力值。
改变PCB的约束状况,会影响PCB的翘曲度和应力水平。若增加对PCB的约束(即装配状态),PCB的翘曲度会明显减小,但应力却相应地增大了,同时在PCB各层之间的分界处易发生应力集中现象,容易造成PCB的开裂或分层。
有限元计算结果表明,阻焊材料热膨胀系数对于PCB的翘曲和应力影响较大,降低其热膨胀系数会显著降低温度荷载下PCB的翘曲度和最大应力值,因此在PCB的设计以及生产过程中,热膨胀系数是非常重要的设计参数。设计参数的选择直接影响PCB的翘曲及应力水平,因而合理的参数选择结果可以显著地降低实际生产中PCB的失效率,从而减少PCB制造和使用成本。

图8 PCB结构翘曲变形云图
3 结束语
本文对PCB的整体结构作了合理的力学简化,建立了有限元分析模型,实现了对PCB结构的数值仿真分析。通过PCB结构多组设计参数的变化,定量分析了不同约束条件下基板厚度、FR-4材料弹性模量、阻焊材料热膨胀系数3种设计参数对PCB翘曲及应力的影响。
计算结果表明,增大PCB的基板厚度和增加FR-4材料的弹性模量均可减小PCB的翘曲,而减小阻焊材料的热膨胀系数不仅可以显著地减小翘曲,还可以在很大程度上降低PCB的应力水平。针对所分析的PCB结构,文中给出了满足装配状态下刚度和强度要求的设计参数选择结果。本文采用的计算仿真方法和参数选择过程对PCB翘曲仿真以及翘曲度和应力水平的控制具有一定的参考价值。
[1]周 斌,潘开林,颜毅林.无铅PCB组件再流焊焊接工艺的热变形仿真分析[J].上海交通大学学报,2007,41(Z2):111-115.
[2]龙庆文,敖荟兰.PCB线宽检测设备的发展现状与趋势[J].印制电路信息,2011(7):66-70.
[3]Hutapea P,Grenestedt J L.Tuning of electric artworks of printed circuit boards to reduce warpage[C]//9th International Symposium on Advanced Packaging Materials:Processes,Properties and Interfaces,2004:230-234.
[4]Nakagawa Y,Yokoyama R.Optimum design of printed circuit board to reduce deformation in reflow process by a global optimization method[J].Materials & Design,2012,33:164-174.
[5]McCaslin L O,Yoon S,Kim H,et al.Methodology for mod-eling substrate warpage using copper trace pattern implementation[J].IEEE Transactions on Advanced Packaging,2009,32(4):740-745.
[6]Hu Guojun,Yong G K,Lim J.Micromechanical analysis of copper trace in printed circuit boards[J].Microelectronics Reliability,2011,51(2):416-424.
[7]Niu Zhongrong,Wendland W L,Wang Xiuxi,et al.A semianalytical algorithm for the evaluation of the nearly singular integrals in three-dimensional boundary element methods[J].Computer Methods in Applied Mechanics and Engineering,2005,194(9/10/11):1057-1074.
[8]周焕林,牛忠荣,王秀喜,等.热弹性力学边界元中二次元的几乎奇异积分计算[J].合肥工业大学学报:自然科学版,2003,26(6):1141-1145.
[9]GJB 362B-2009,刚性印制版通用规范[S].
