二维非等长图像置乱方法的研究与验证

陈 曦， 向 菲， 张志勇， 王 剑

（河南科技大学 电子信息工程学院，河南 洛阳 471023）

0 引 言

近年来，随着各种通信技术的不断发展和应用，图像等多媒体信息的处理成为研究人员关注的重要方向，信息的安全也日益受到人们的重视。考虑到图像信息的一些特征，目前提出了基于混沌与元胞自动机的图像加密技术［1］、基于SCAN语言的加密技术［2］、并行的图像加密技术［3］、基于空间混沌的加密技术［4］及基于高维混沌的加密技术［5－6］等多种关于图像加密领域的方法。

基于像素矩阵变换的加密技术是一种最简单的图像加密技术，比较经典的有：Arnold变换［7］、Baker变换及幻方变换等［8］。这些变换方法可以视为对像素矩阵进行拉伸、压缩、折叠及拼接的过程，通过这一系列手段对数字图像像素矩阵中的点进行重新排列。由于数字图像是有限点集，这种反复变换在一定次数内像素点的位置会出现相当程度的混乱，但是由于有限点集的重复迭代在本质上是有周期性的，因而系统在经过有限次的迭代后会出现庞加莱回复性，为逆变换提供了依据。

然而以上置乱方法通常用于正方形图像的处理，对于非等长的普通矩形图像，由于其不具备普遍的变换周期，导致逆变换难以实现。文献［9］通过简单的扩展方法将非等长图像变为正方形图像，以作为Arnold变换的预处理，再运用Arnold变换进行置乱变换，这种简单扩展图像矩阵的方法增加了图像的信息；文献［10］给出了多维等长Arnold变换及Fibonacci－Q变换处理非等长图像的方法，尽管所提方法不需对像素矩阵扩展，但由于置乱仅针对灰度，因而对剪切和擦除等攻击不具备全局分散能力；文献［11］通过推导得出图像高宽比M／N为整数时Arnold变换周期存在的结论，拓展了Arnold变换的应用范围；文献［12］在文献［11］的基础上找到了一个适用于任意高宽比图像的普适Arnold变换矩阵，并证明了其周期存在性。

但是，在设计数字水印图像以及图像的反置乱过程中，运用周期性进行反变换是一种效率较低的方法，这也限制了水印图像的大小，因此文献［13］提出了快速的反变换算法。本文在上述研究的基础上，采用一种基于图像区域一致性的图像插值方法对非等长图像进行预处理，以使得能够运用Arnold变换及其快速反变换方法对其进行置乱与逆置乱，提高了效率，扩大了经典图像置乱方法的应用范围。

1 二维Arnold变换及其快速反变换

对于N×N图像像素矩阵，各个点的像素坐标可以表示为（x，y），x，y＝0，1，2，…，N－1，若存在（x，y）到（x′，y′）的映射，且满足（1）式，则称其为二维图像的Arnold变换。

（1）式为：

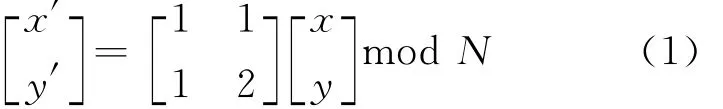
由（1）式可得：

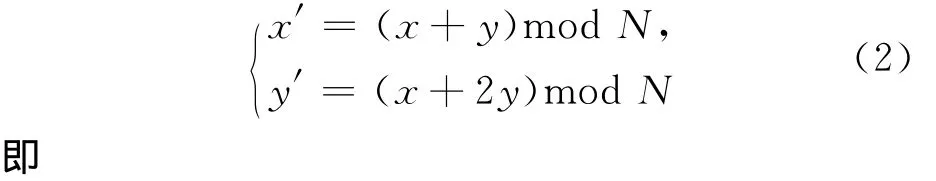
由于图像的周期性与像素矩阵的大小密切相关，运用周期性对图像进行反变换会导致运行时间及计算量的增加。根据文献［12］，在像素矩阵中有：

由不等式性质可得：

所以p取0和1，q取0、1和2。由（4）～（6）式可得：

所以有：

（1）x′≤y′时，有y′－x′≥0，p＝q，则有y＝y′－x′，若x′≤y，那么x＝n＋x′－y，反之则有x＝x′－y；

（2）x′＞y′时，有y′－x′＜0，p＝q－1，则y＝n＋y′－x′，同上可求得x。

以上即为Arnold快速反变换的算法原理。

2 基于区域一致性的图像插值技术

本文采用一种基于区域一致性的方法进行图像插值处理［14］，图像插值示意图如图1所示，设图1a初始图像中A、B、C、D4点的坐标分别为（x，y）、（x＋1，y）、（x，y＋1）及（x＋1，y＋1），图2b为进行插值后的图像，根据缩放倍数，在区域e、f、g、h和i插入相应个数的像素点；图1c中，插入的像素点M（x1，y1）映射到原图的位置具有以下3种情况：

（1）当dx＝0且dy＝0时，（x1，y1）＝（x，y），即A点。

（2）如果dx≠0、dy＝0或dx＝0、dy≠0，（x1，y1）位于e或f区域（根据M 点位置可能映射到h或i区域）。

（3）若dx≠0且dy≠0，则位于区域g。

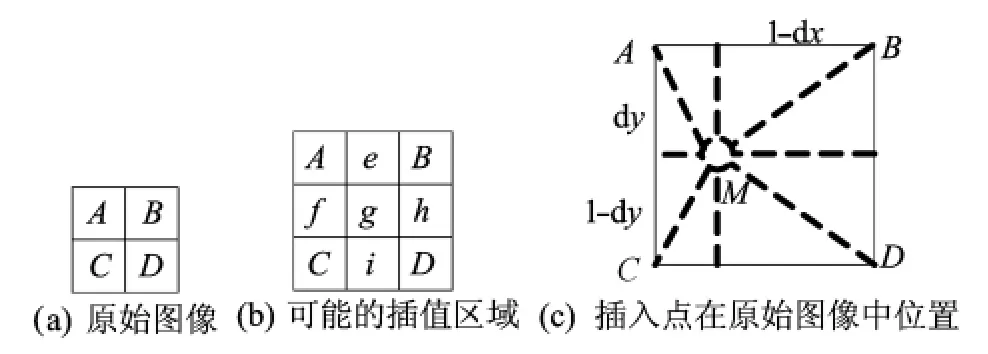
图1 图像插值示意图

根据区域标记w选择适用的插值方式。对于区域e的点，当A和B的标记相同时，为区域内部点，采用一维线性插值公式即（9）式；否则为区域间过渡插点，采用一维非线性插值公式即（10）式。同样地，f、h和i区域采用相同的方法。对于区域g内的点，当A、B、C、D4点的标记都相同时，为区域内的点，采用二维线性插值公式即（11）式；否则为过渡点，采用二维非线性插值公式即（12）式。

（10）式～（13）式如下：

其中，I00、I10、I01及I11分别表示I（x，y）、I（x＋1，y）、I（x，y＋1）和I（x＋1，y＋1）；w00、w01、w10和w11分别代表w（x，y）、w（x，y＋1）、w（x＋1，y）和w（x＋1，y＋1）。

3 实验结果

本文对方案进行实验验证，利用Arnold变换对任意宽高比矩形图像进行置乱处理的方法流程如图2所示。根据这种方法对Matlab标准库中的一些非等长灰度图像进行了处理，board图像进行10轮像素位置置乱变换及反变换的结果如图3所示。

图2 任意矩形图像的Arnold变换

图3 非等长图像的处理图像

本文采用均方误差 MSE、峰值信噪比PSNR、信噪比SNR、平均梯度AG以及结构相似度SSIM［15］等参数对处理结果进行分析比较。采用本文方法对部分Matlab标准图像库中非等长矩形图像进行处理后的图像质量见表1所列。

表1 处理后图像质量分析

与文献［11］和文献［12］中对非等长矩形图像的Arnold置乱方法相比，本文方法能够使用快速反变换方法［13］，使得逆置乱的过程中不需要考虑像素矩阵的大小，即摒弃了采用周期性进行多次重复迭代的过程，因此在运行过程中显然具有更高的效率。

对于一幅256×256大小的图像，在一台具有2.53GHz工作主频的CPU、2GB内存容量的个人电脑上进行1轮Arnold正变换所需时间约为0.019380s，若根据周期性进行逆置乱则相当于进 行 192 次 Arnold 迭代 运 算［16］，耗 时 约3.72096s，而相应地采用快速逆置乱方法只需进行1轮逆置乱即可得到原始图像，所需时间仅为0.006195s。

从上述结果可以看出，利用本文方法首先对非等长矩形图像进行预处理，然后再进行置乱及逆置乱，具有较好的图像质量及更快的处理速度，能够付诸实践。

4 结束语

本文将图像插值的方法应用于改进图像置乱算法，可以广泛运用于Arnold变换、Baker变换、幻方变换等仅能处理正方形的传统置乱方法，使得其能够应用于更具有一般性的非等长矩形图像的处理中。

虽然Arnold算法能够很好地对图像像素位置进行置乱变换，但是由于该变换具有庞加莱回复性，导致该算法在安全性方面具有明显的漏洞，因此，不能以该算法为基础构成独立的加密系统。根据经典的Shannon加密理论［17］，加密系统须由置乱和混淆2部分构成，由本文所提出的对非等长图像进行Arnold变换的方法组成，并综合运用置乱混淆思想的完整加密系统将在后续工作中陆续提出。

［1］彭 川，李元香.基于混沌和细胞自动机的图像加密算法［J］.计算机工程与设计，2012，33（7）：2526－2529，2535.

［2］Maniccam S S，Bourbakis N G.Lossless image compression and encryption using SCAN［J］.Pattern Recognition，2001，34（6）：1229－1245.

［3］刘 君，周 庆，胡 月.一种新的图像加密并行算法［J］.计算机工程，2010，36（11）：20－21，24.

［4］刘树堂，孙福艳.基于空间混沌的图像加密设计［J］.中国科学：G辑，2009，39（3）：387－393.

［5］许 冰，孙永维，李 洋，等.基于高维混沌系统的图像加密改进算法［J］.吉林大学学报：信息科学版，2012，30（1）：12－17.

［6］杨 钒，薛模根.复合混沌二级置乱图像加密算法研究［J］.合肥工业大学学报：自然科学版，2009，32（8）：1128－1131.

［7］Ye Ruisong.A novel image scrambling and watermarking scheme based on orbits of arnold transform［C］／／Proc of Pacific－Asia Conference on Circuits，Communications and Systems，2009：485－488.

［8］Zhang Li，Ji Shiming，Xie Yi，et al.Principle of image encrypting algorithm based on magic cube transformation［J］.Lecture Notes in Computer Science，2005，3802（1）：977－982.

［9］王冬梅.2维Arnold变换加密数字全息图［J］.浙江工业大学学报，2004，32（3）：272－276.

［10］Qi Dongxu，Zou Jiancheng，Han Xiaoyou.A new class of scrambling transformation and its application in the image information covering［J］.Science in China Series E：Technological Sciences，2000，43（3）：304－312.

［11］邵利平，覃 征.二维非等长图像置乱变换［J］.电子学报，2007，35（7）：1290－1294.

［12］李永逵，冯乔生，周 粉，等.二维Arnold变换及非等长图像置乱［J］.计算机工程与设计，2009，30（13）：3133－3135.

［13］孔 涛，张 亶.Arnold反变换的一种新算法［J］.软件学报，2004，15（10）：1558－1564.

［14］符 祥，郭宝龙.区域指导的自适应图像插值算法［J］.光电子激光，2008，19（2）：233－236.

［15］Wang Z，Bovik A C，Sheikh H R，et al.Image quality assessment：from error visibility to structural similarity［J］.IEEE Transactions on Image Processing，2004，13（4）：600－612.

［16］孙燮华，章仁江.计算Arnold变换周期的新算法［J］.计算机技术与发展，2008，18（11）：66－68.

［17］Shannon C E.Communication theory of secrecy systems［J］.Bell System Technology Journal，1949，28：656－715.