基于虚拟样机的BGA供球机构动态性能仿真研究
2013-09-28田晓青吴路路
夏 链, 吴 斌, 田晓青, 吴路路, 韩 江
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
植球机是BGA(Ball-Grid-Array,简称BGA)球栅阵列封装技术设备[1]中的核心部分,主要完成BGA封装中的助焊剂涂敷、焊料球贴放、检测和固化等工序[2]。在这些工序中最为复杂和重要的是焊料球贴放,实现此工序动作的机构为植球机中的关键部件供球机构,供球机构是否能够准确而又可靠地实现焊料球贴放工序,直接关系到BGA封装的成功与否。
供球机构完成的动作有焊料球的供给、焊料球的放置以及多余焊料球的回仓,对其动态性能要求极高。焊料球直径很小而且质量很轻,要确保在供球机构一个运动循环周期内均匀分布于模板孔中,而且不会出现丢球的现象。
针对上述问题,本文以ADAMS软件为辅助手段,建立了供球机构的虚拟样机模型,研究供球机构的动态性能,在机构设计阶段就能得知焊料球在一个循环周期内的运动状态,发现原产品设计可能存在的不合理之处,并提出改进措施。
1 供球机构虚拟样机模型的建立
1.1 模型的简化及焊料球的确定
本文利用Pro/E Wildfire 5.0软件建立供球机构的三维装配体模型,在导入ADAMS软件前对模型进行了简化处理,如删除了尺寸较小的倒角、圆角及通孔。因模板中放置焊料球的小孔较多,而且焊料球在供球机构工作流程中的状态比较复杂,为了进一步简化仿真模型及仿真计算量[3],在分析之前做以下简化:
(1)考虑一个焊料球在一堆焊料球中的状况,只研究位于模板孔中焊料球在往复摆动时的情况。
(2)不考虑模板中每一个小孔内各个焊料球的情况,只研究离翻板回转中心最远的中间阵列焊料球的情况。
焊料球质心坐标如图1所示,焊料球和模板之间的位置关系如图2所示。

图1 焊料球质心坐标系示意图

图2 焊料球和模板位置关系
1.2 接触碰撞理论基础及参数的选取
当构件表面之间出现了接触碰撞现象,构件表面之间的接触力也就随即产生。构件表面之间的接触主要有2种类型,一种是构件之间的接触时断时触,另一种是构件之间连续接触,没有分离[2]。
对于本文研究的供球机构,焊料球和模板之间的接触类型属于第1种。ADAMS软件计算接触力有2种方法:①Impact计算方法,需定义的参数主要有刚度系数和阻尼系数;②Restitution计算方法,需定义的参数主要有恢复系数。考虑到焊料球与模板之间是弹性碰撞接触,本文选用Impact函数计算焊料球与模板之间的接触力,Impact函数表达式[4]为:

其中,p为2个要接触构件的实际距离;v为发生碰撞时2个构件的相对速度;p0为2个构件接触的参考距离;k为刚度系数;e为碰撞力指数;Cmax为最大阻尼率;d为阻尼率达到最大所要经过的距离,用来防止碰撞过程中阻尼条件不连续,又被称为惩罚深度;step为1/2正矢阶梯函数。
当p0>p时,2个构件发生接触碰撞,反之Impact函数无效,即2个物体不发生碰撞,其碰撞力为0。刚度系数可根据Hertz碰撞理论进行求解,根据焊料球和模板的材料属性,两者之间的接触定义参数如下:
(1)计算接触力方法为冲击函数法,其接触刚度为1.0×108N/mm,力指数为1.5,阻尼为1.0×104N·s/mm,切入深度为1.0×104mm。
(2)计算摩擦力方法为库伦法,其静态、动态系数分别为0.2、0.05,静、动滑移速度分别为0.1、1.0mm/s。
1.3 样机模型约束和重力的施加
将供球机构装配模型导入ADAMS软件后,自动生成该机构无约束的虚拟样机模型。采用几何和密度方法修改样机模型质量属性,按照供球机构实际运动状态对其施加相应的约束、接触力以及重力,至此,建立了供球机构的虚拟样机模型,如图3所示。
ADAMS软件根据刚体各自的质量属性、质心坐标系和约束,自动生成样机的动力学模型,其算法程序运用了Gear的刚性积分算法以及稀疏矩阵技术,能够大大提高计算效率[5]。

图3 供球机构虚拟样机模型
2 供球机构时序图的确定
时序图是以某一主要执行机构的工作起点为基准,表示各执行机构的运动循环相对于该主要执行机构而动作的先后次序,从而既可以达到互相协调的目的,又可以最大限度地缩短机器的运动循环周期,以提高生产率[5]。供球机构包括3个原动件,分别为刷球电机、翻板电机和气缸,其中气缸和刷球电机都包括行程和回程2个动作。根据设计要求及工艺,确定一个循环周期内工艺循环动作时序图,如图4所示。本文不考虑对仿真结果影响很小的刷球电机和气缸的运动,分析研究翻板电机在一个循环周期内供球机构的动态性能。

图4 供球机构时序图
3 供球机构动态仿真
3.1 T型加减速下动态性能分析
T型加减速是伺服电机加减速控制中较为简单的一种,电机瞬时速度计算公式[6]为:

其中,vi+1为当前电机瞬时速度;vi为前某一时间电机的瞬时速度;a为电机的加速度;t为时间。
由图4及翻板在一个运动循环周期内最大的上下倾角,结合ADAMS中的函数库,确定在T型加减速方式下供球机构虚拟样机中定义的翻板电机驱动函数表达式,即

其中,ω(t)为翻板电机的角速度;t为时间。
仿真结果[7-9]如图5~图8所示。

图5 T型加减速下焊料球y向位移曲线
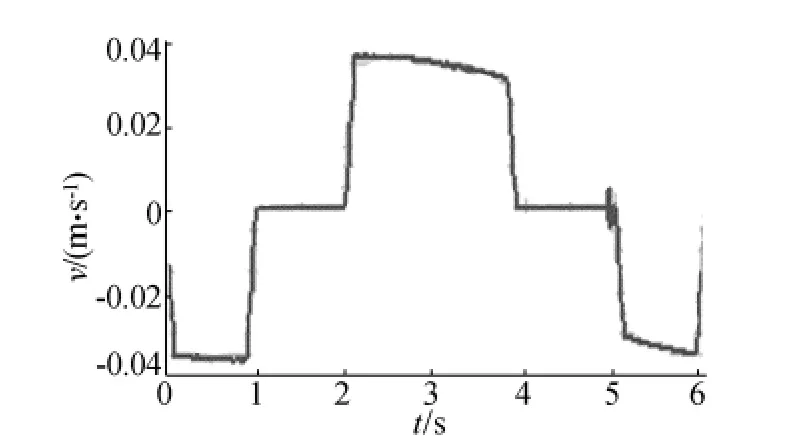
图6 T型加减速下焊料球y向速度曲线

图7 T型加减速下焊料球y向加速度曲线

图8 T型加减速下模板对焊料球合力曲线
由图5可知,焊料球在y方向位移曲线最能反映翻板的运动过程,焊料球从最下倾角位置到最上倾角位置的行程约为0.0648m。从图6中可以看出,焊料球的速度只有在电机处于加减速状态下变化较大,其余时间则相对较平稳,说明电机处于匀速状态时,有利于焊料球处于较平稳的运动状态,在0~0.1s内焊料球速度从0加速到最大值0.0354m/s。
从图7中可以看出,焊料球在y向上加速度波动较多,且最大加速度突变值出现在0.84s,其值达到了93.4m/s2。
通过计算,求得焊料球的重力大小约为0.462×10-5N。从图8中可以看出,焊料球在大部分时间所受模板对其合力约等于焊料球所受到的自身重力,说明焊料球在大部分时间内基本处于受力平衡的状态。
合力最大突变时刻和加速度最大突变时刻一样,出现在0.84s,此时刻焊料球受到模板对其最大合力约为4.86×10-5N,远远大于焊料球本身的重力。
3.2 S型加减速下动态性能分析
S型加减速就是伺服电机在加减速阶段的速度曲线形状呈S形,一般正常情况下的S曲线加减速的运行过程可分为7段,即加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段。
伺服电机正反向的负载驱动能力可认为是一致的,因此可以假设伺服电机的正向和反向最大加速度相等,均为amax。这时,可以假设伺服电机加速度从0达到其最大值和从其最大值到0所用的时间相等,此时间定为该电机的一个特性时间常数τ,应该满足τ≤vmax/amax,如取τ=vmax/2amax,则有:
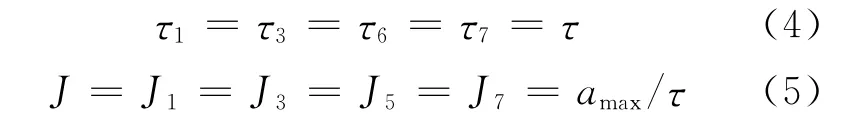
其中,(4)式成立的前提条件是在运行过程中能够达到最大加速度,如果这个前提条件达不到,则(4)式将由(5)式代替。
由图4及翻板在一个运动循环周期内最大的上下倾角,结合ADAMS中的函数库,确定在S型加减速方式下供球机构虚拟样机中定义的翻板电机驱动函数表达式,即
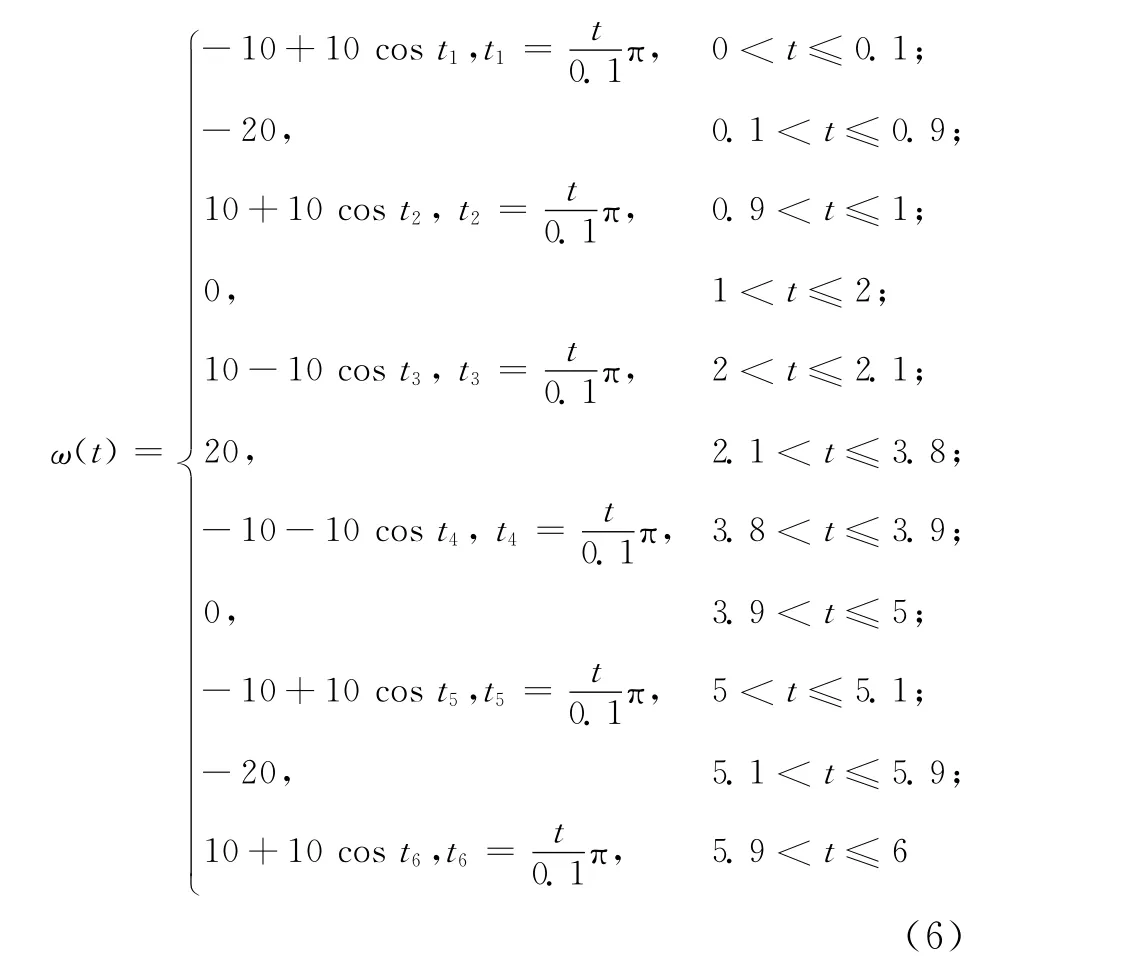
仿真结果如图9~图12所示。
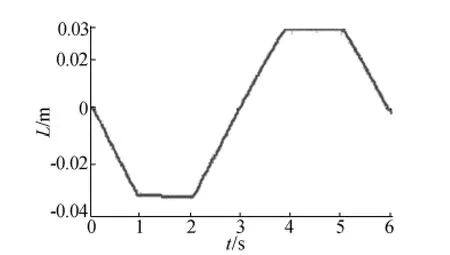
图9 S型加减速下焊料球y向位移曲线
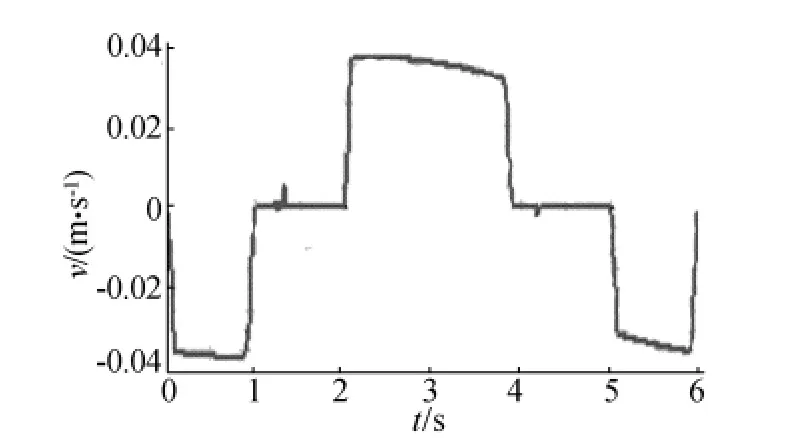
图10 S型加减速下焊料球y向速度曲线
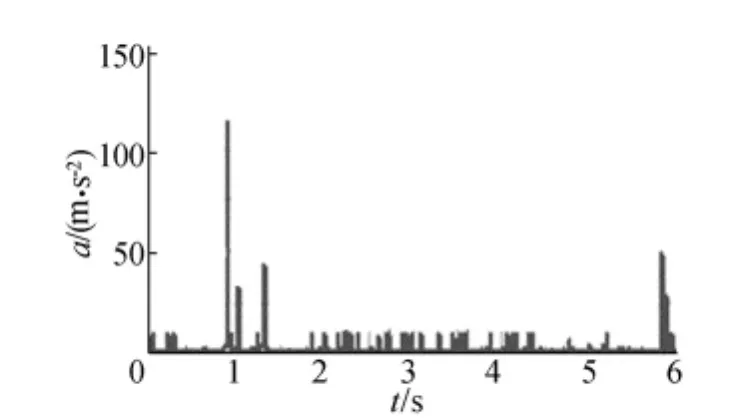
图11 S型加减速下焊料球y向加速度曲线

图12 S型加减速方式下模板对焊料球合力曲线
对比处于2种加减速方式下的动态性能,电机处于T型加减速控制方式相对较简单,而其速度和加速度都不如电机处于S型加减速控制方式平稳,即电机处于S型加减速这种控制方式更有利于焊料球处于稳定的状态。2种控制方式下都存在某一时刻模板的合力数值远远大于其重力,这个时刻焊料球极不稳定,在实际过程中难以保证顺利完成封装工序,此时可以在机构设计中考虑采取真空吸头吸附焊料球,使焊料球在工作过程中的状态更加平稳。
4 结束语
本文以接触碰撞理论为理论依据,根据模型简化原理,建立了供球机构的虚拟样机模型。根据供球机构物理样机的工艺动作,确定了供球机构虚拟样机模型的工艺循环时序图。根据电机的2种驱动方式,利用ADAMS分别对其进行动态仿真,对结果进行了对比,并得出了结论,为企业的生产制造提供了可靠的理论依据。同时本文也存在一些不足,如没有考虑到供球机构中刷球电机的运动,缺少进一步实验论证。
[1]Han C W,Oh C M,Hong W S.Prognostics model development of GBA assembly under vibration environment[J].IEEE Transactions on Components,Packaging and Manufacturing Technology,2012,2:1329-1334.
[2]刘劲松,郭 俭.BGA/CSP封装技术的研究[J].哈尔滨工业大学学报,2003,35(5):602-604.
[3]Erich R,Coyle R J,Wenger G M,et al.Shear testing and failure mode analysis for evaluation of BGA ball attachment[C]//Twenty-Fourth IEEE/CPMT Electronics Manufacturing Technology Symposium,1999:16-22.
[4]李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2006:91-96.
[5]郑文纬,吴克坚.机械原理[M].北京:高等教育出版社,1996:331-344.
[6]胡建华,廖文和,周儒荣.CNC系统中几种升降速控制曲线的研究与比较[J].南京航空航天大学学报,1996,31(6):706-711.
[7]常玉连,郡守君,高 胜,等.基于虚拟样机的井下机器人行走仿真实验[J].系统仿真学报,2008,20(13):3610-3613,3621.
[8]岳双杰,范秀敏,马彦君,等.圆锥破碎机虚拟样机参数化建模与仿真优化[J].中国机械工程,2011,22(22):2712-2716.
[9]余道洋,韩 江,夏 链.螺旋转子数控加工的数学建模分析与研究[J].合肥工业大学学报:自然科学版,2007,30(11):1433-1435.
