基于直觉模糊集合的大学生综合素质评价
2013-09-28孙晓玲
孙晓玲, 王 宁
(合肥师范学院 数学系,安徽 合肥 230601)
0 引 言
大学生综合素质测评是对大学生的一种评价指标,内容通常包括德育测评、智育测评、体育测评和能力测评4个方面。科学有效的测评方法不但可以促进高校素质教育的发展,使学生在素质发展上进一步明确今后努力的方向,还可以有效地促进学校学生工作更加规范化和科学化。由于大学生综合素质评价的因素较多,并且大都有一定程度的模糊性,因此已有的关于大学生综合素质测评的方法大都是采用以模糊集合为基础的模糊综合评判的方法[1-2]。
由于模糊集合存在不能完整描述不确定信息的局限性,已有的评价方法中模糊集的隶属函数值只能是一个单一的表示隶属度的值。但事实上,在对学生进行综合测评的过程中,一些作为测评评委的教师或学生可能对测评对象符合某些评价指标的程度不太确定,或者说存在一定程度的犹豫,这个犹豫的信息是以模糊集合为基础的模糊综合评价方法所不能描述的。
本文将直觉模糊集合引入到大学生综合素质测评中,利用直觉模糊集合能充分描述不确定信息的优越性,在测评方法中体现评委对评价对象的某些评价指标表示支持、反对和犹豫程度的信息,给出基于直觉模糊集合的大学生综合素质评价方法。
1 直觉模糊集合(IFS)
Atanassov所提出的直觉模糊集合是对扎德所提出的传统模糊集合的扩展。在实际问题中,常会出现人们对元素a属于集合A的程度没有绝对把握的情形,直觉模糊集合正是源于这种情况而产生的。由于它可以描述元素a属于集合A、不属于集合A以及不确定的程度,因此直觉模糊集相比于传统模糊集合在描述不确定信息方面有更强的优越性。下面介绍直觉模糊集合的基本定义和定理。
假设有限非空集合 X={x1,x2,…,xn}为论域,F(X)为X上的所有模糊集所构成的集合。若A∈F(X),x∈X,则A(x)表示元素x对集合A的隶属度。若A为清晰集,则对任意的x∈X,A(x)只能等于1或0。
直觉模糊集合定义如下。
定义1 假设X为论域,则X上的直觉模糊集合为:

其中,函数μA(x):X→[0,1]和γA(x):X→[0,1]分别表示集合A的隶属度函数和非隶属度函数。集合A上每一x∈X,都有0≤μA(x)+γA(x)≤1。由集合A的隶属度函数μA(x)和非隶属度函数γA(x)所组成的有序函数对(μA(x),γA(x))称作直觉模糊数[3]。
由该定义可以看出,传统模糊集合也可写成直觉模糊集:
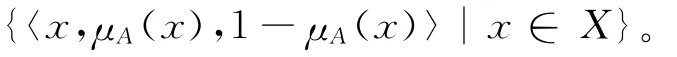
若A为清晰集,则对任意的x∈X,一定有μA(x)=0,γA(x)=1或者μA(x)=1,γA(x)=0。
定义2 对论域X中的任一直觉模糊集A,称πA=1-μA(x)-γA(x)为直觉模糊集A 中元素x的直觉指数,它是元素x对直觉模糊集A的犹豫程度的度量,表示X中的元素x属于A的不确定程度或犹豫程度。显然,对任一x∈X,0≤πA(x)≤1,论域X 中的每个传统模糊子集B,必有:
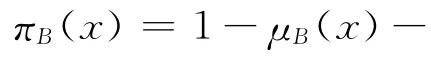

由此可看出,扎德的传统模糊集合是直觉模糊集的一个特例[3]。
由定义1和定义2可以看出,对于X中的直觉模糊集A,其隶属度μA(x)、非隶属度γA(x)以及直觉指数πA(x)可分别表示元素x属于直觉模糊集A的支持、反对、中立3种证据的程度。
定义3 设A={〈x,μA(x),γA(x)〉|x∈X},B={〈x,μB(x),γB(x)〉|x∈X}为论域 X 上的直觉模糊集,则有以下2种关系[3]:
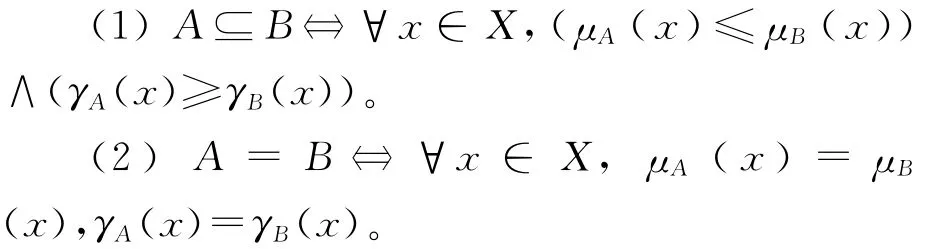
定义4 假设A、B都是论域X上的直觉模糊集合,则有以下2种运算:

2 大学生综合素质评价模型
大学生综合素质的评价指标比较多,可分为一级评价指标和二级评价指标。其中一级评价指标包括德、智、体、能4个方面,针对一级指标可以建立二级评价指标集,从而构成二级直觉综合评价体系,评价体系如图1所示[4]。

图1 大学生综合素质评价体系
若用直觉模糊集合作为载体,评价对象(某大学生)Ai关于评价指标xj的评价结果可以表示为[μAi(xj),γAi(xj)]。其中,μAi(xj)表示评价对象Ai符合评价指标xj的程度;γAi(xj)表示评价对象Ai不符合评价指标xj的程度;πAi(xj)=1-μAi(xj)-γAi(xj)表示评价对象Ai符合评价指标xj的犹豫程度,其中,μAi(xj)∈[0,1],γAi(xj)∈[0,1],且μAi(xj)+γAi(xj)≤1。
例如,20位学生和教师评委对学生Ai关于“遵守校规校纪”这个评价指标进行评测,为方便起见,只需各位评委对学生Ai“符合”或“不符合”进行投票即可,投票的结果是投“符合”票的12人,投“不符合”票的6人,还有2人弃权,则对学生Ai关于评价指标“遵守校规校纪”的测评结果可以表示为(0.6,0.3),其中1-0.6-0.3=0.1可以视为评委关于该项评价指标的犹豫程度。
2.1 TOPSIS算法
模糊TOPSIS是由Hwang和Yoon最早提出的多指标决策方法,又称作理想解法。该方法是根据评价指标与其理想解和负理想解之间的距离来评价对象符合该评价指标程度的[5]。在本文中,理想解和负理想解可分别记作x+和x-。
在直觉模糊集合中,评价指标xj的理想解x+可写作{(xj,1,0)|xj∈X},其中评价对象 Ai对于评价指标xj的隶属度和非隶属度分别为1和0。类似地,任何评价指标xj的负理想解x-可记作{(xj,0,1)|xj∈X},这时,评价对象Ai对于评价指标xj的隶属度和非隶属度分别为0和1[6-7]。
设(μAi(xj),γAi(xj))是评价对象 Ai关于评价指标xj的评价结果的直觉模糊集,其中μAi(xj)表示评价对象Ai符合评价指标xj的程度,而γAi(xj)表示评价对象Ai不符合评价指标xj的程度,则评价对象Ai关于评价指标xj分别与其理想解x+与负理想解x-之间的距离为:

根据(1)式、(2)式,可计算出评价对象Ai关于评价指标xj与其理想解的相对贴近度为:

由于d(Ai,x+)≥0,d(Ai,x-)≥0,因此,显然Di∈[0,1]。
计算出各个评价对象与理想解的相对贴近度后,可以通过对这些相对贴近度进行排序,从而得出评价对象的排名,Di值越大,评价对象Ai越优秀。
2.2 大学生直觉综合素质评价
基于直觉模糊集合的TOPSIS大学生直觉综合素质测评步骤如下:
(1)建立评价指标体系。首先根据层次化的方法对影响评价的各个指标进行分类,建立评价指标体系,如图1所示,其中,xi(i=1,2,…,m)为一级评价指标,xij(j=1,2,…,ni)为一级指标xi下所属的二级评价指标。
(2)给各个评价指标赋予权值。由于在评价指标体系中,各个评价指标对于评价结果的重要性有所不同,需赋予不同的权值。赋权的方法较多,常用的有模糊熵权法、德尔菲法和层次分析法等,这里可以采用文献[8]中给出的模糊熵权法确定各二级评价指标的权重 w1,w2,…,wn,其中=1,n为所有二级指标的个数。
(3)构造直觉模糊集合(IFS)评价矩阵。根据测评小组给出的评价对象Ai关于评价指标xj的评价结果(μAi(xj),γAi(xj)),构造直觉模糊集合(IFS)评价矩阵。
(4)计算距离、相对贴近度。根据TOPSIS方法中的(1)式、(2)式计算评价对象分别与其理想解和负理想解的距离,再根据(3)式计算评价对象与其理想解的相对贴近度。
(5)得出结论。对步骤(4)中所得的相对贴近度进行排序,相对贴近度大者所对应的评价对象为优。
3 实 例
采用基于直觉模糊集合的TOPSIS大学生直觉综合素质测评方法对某师范大学的学生进行综合测评,为简便起见,仅选择3位大学生A1、A2、A3作为评价对象,步骤如下。
(1)根据层次化方法针对该校大学生建立图1所示的综合测评指标体系。
(2)为各个二级评价指标赋予权值。根据文献[7]中所提供的模糊熵权法分配给12个二级评价指标的权值分别为:


(3)构造IFS评价矩阵。根据测评小组中所有成员的意见,得到IFS评价矩阵,见表1所列。

表1 IFS评价矩阵
(4)计算距离、相对贴近度。评价对象A1、A2、A3分别与其理想解和负理想解的距离以及与其理想解的相对贴近度可利用Matlab软件进行仿真计算,计算结果见表2所列。
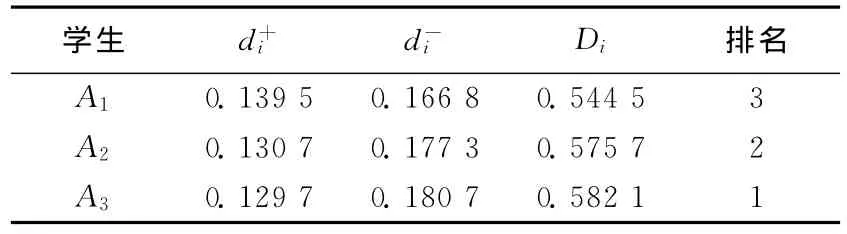
表2 距离、相对贴近度
(5)得出结论。由表2可以看出,3位大学生综合素质测评的排名为A3>A2>A1,表明第3位学生的综合素质水平最高,第2位学生次之。
4 结束语
本文以直觉模糊集合为工具,根据评价对象分别与其理想解、负理想解之间的距离,评价对象与理想解的相对贴近度以及TOPSIS方法,有效地计算出大学生综合素质直觉模糊测评值。由于可利用Matlab软件进行仿真计算,因此与模糊综合评价方法相比,计算过程更加高效,测评结果更加科学合理。
[1]孙 艳,蔡志丹.模糊综合评判法在学生考试成绩评价中的应用[J].长春理工大学学报:自然科学版,2011,34(4):178-179.
[2]梅家斌,曹剑文,王 丽.大学生专业素质现状调查及模糊综合评价[J].武汉科技学院学报,2009,22(4):38-40.
[3]Yager R R.Level sets and the representation theorem for intuitionistic fuzzy sets[J].Soft Comput,2010,14:1—7.
[4]王 宁,孙晓玲,梁 艳.综合素质评价的神经网络模型及Simulink实现[J].合肥师范学院学报,2011,29(6):15-19.
[5]陈 奎,张天云,闫 娜,等.理想解法的改进及其在工程材料综合评价中的应用[J].机械工程材料,2012(2):96-99.
[6]Baki A,Guveli E.Evaluation of a web based mathematics teaching material on the subject of functions[J].Computers&Education,2008,51:854-863.
[7]Marriott P.Students’evaluation of the use of online summative assessment on an undergraduate nancial accounting module[J].British Journal of Educational Technology,2009,40:237-254.
[8]陈庆伟.应用直觉模糊熵权法评价医疗质量[J].数理医药学杂志,2010,23(4):485-486.
