包边注塑的浇口位置对黏合撕裂强度的影响

王乾廷， 刘 琼， 刘贤平，2， 陈文哲

（1.福建工程学院 材料科学与工程系 福建 福州 350108；2.福耀玻璃工业集团股份有限公司 福建 福州 350301）

塑料包边玻璃多用在汽车侧窗、角窗和前、后挡风安全玻璃中，与车体紧密地结合，提高密封性，同时增强美观。生产流程是先把普通退火玻璃钢化，然后把玻璃作为嵌件，在其边缘注射进熔化的塑料，固化后塑料紧包在玻璃边缘形成包边［1－2］。

包边注塑生产工艺与常规的塑料注射成型工艺相似，每个注射周期包括充模、补料、倒流和浇口封闭后的冷却共4个阶段。但包边注塑也具有自身的特殊性，主要体现在：① 塑件的断面小、长度长且结构复杂，属于受限空间的注塑成型，易出现成型缺陷；② 玻璃作为嵌件承受热冲击和力冲击，易变形或破碎；③ 塑料和玻璃2类材料之间需要可靠黏结，避免脱落或虚连的情况。在现有技术水平下，这些问题使该类型产品的废品率居高不下。由于包边玻璃生产技术长期被国外垄断，因此相关的技术成果报道有限［1－4］。

包边的过程，本质是参与包边的对象之间的质量、能量和动量传递的过程［5－7］。要保障包边注塑的成型质量，需在流变学设计、传热学设计和力学设计3个方面深入研究［8－9］。包边的质量评价指标众多，其中塑料与玻璃的异质材料之间黏合度、包边塑件的分子链取向是2个重要的考察指标［5，7］。

由于玻璃的形状千变万化，包边的材料和几何形状也多种多样，因此，以某一形式的玻璃为研究对象不具备普遍意义，需要抽象出简化模型，通过试验和理论分析的方法研究传递规律。

本文考察包边注塑的浇口位置对黏合撕裂强度的影响情况，在建立玻璃塑料包边注射成型的简化试验模型的基础上，设定可行的浇口形式，测定熔体温度和压力的变化曲线，推导能量传递情况；根据包边塑料的自身性质和撕裂强度测试情况，分析浇口位置对黏合强度的影响机理。

1 简化模型和基本假设

1.1 简化模型

包边玻璃的结构如图1所示。不同位置的剖面的形状和面积一般不等，面积从几到数百平方毫米不等。塑料包边注射成型时，多采用立式注塑机，并辅以特殊的玻璃定位和夹紧机构，以防止注射成型过程中玻璃产生位移而报废。根据包边注塑的生产实践，建立如图2所示的包边注塑简化模型。简化模型的优点是不受具体的玻璃型号和规格限制，对研究玻璃包边注塑具有普适性；塑料包边宽度b≪L，可以直接引入受限空间内的熔体流动理论进行分析；实际生产中玻璃和包边的变化可以在推导的公式中添加形状因子加以修正。不足之处在于多数汽车玻璃的轮廓是不规则的，这里简化为长直线边，与实际情况有一定的偏差，特别是在转角过渡处，影响分析的误差；未考虑包边断面形状的突变，需要另外对这种情况进行研究。

图1 包边玻璃示意图

图2 玻璃包边简化试验模型

1.2 基本假设

（1）玻璃本身为弧形曲面，轮廓也为弧线，曲率半径均较大（约为1250mm）。为简化研究，玻璃各边的曲线及玻璃曲面均假设为直线和平面表示。

（2）假设熔融态的包边塑料PVC和冷却水均为不可压缩流体。

（3）忽略浇口和流道系统对于外界的传热，并假设熔融态的PVC密度ρ、热导率λ和比热c均为常数［3］。

（4）PVC的黏性η采用修正的Bird－Carreau－Yasuda模型［3，10］，即

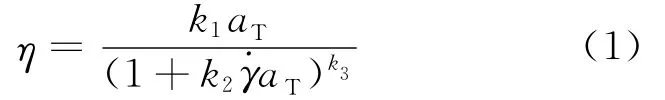
其中，k1～k3均为材料常数；˙γ 为等效剪切率；aT为转换系数，表达式［11］为：

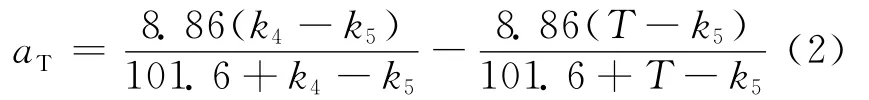
其中，T为熔体温度；k4和k5为材料常数。

2 包边注塑的传递方程

熔融PVC流动的质量、动量和能量方程分别［10］为：

其中，v为熔体流速；t为时间；p为压力；τ为黏性剪切应力。

在PVC熔体和玻璃之间的界面处，设μ为运动黏度，用下标“a”和“g”分别代表空气和玻璃的参数，设k是一个权重因子，0＜k＜1，则有：

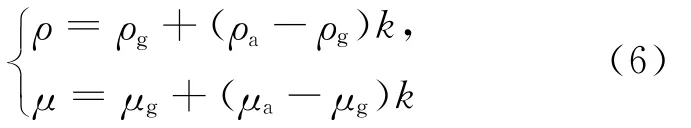
当某点位于塑料熔体表面时k取1，位于玻璃表面时k取0。在塑料熔体固化过程中，位于熔体液面上位置处的传热与（5）式相比，多出放热项Sc，表示为：

其中，H为熔体的熔化潜热；fs为熔体的固化比率。当T＞ Tf时，fs（T）＝0（熔融塑料区）；当T＝Tf时，0＜fs＜1（等温相变区）；当T＜ Tf时，fs（T）＝1（固化塑料区）。

在充填阶段，假定高分子材料的流动率和浇口温度均为常数，熔体流速连续；在冷却阶段，假定浇口处为零速率且为绝热边界条件。

3 试验方法

在东华FX100精密注塑机上进行包边成型试验，对厚度为3.2mm的钢化玻璃进行包边。包边塑料采用非反应性注塑包边PVC（聚氯乙烯），包边注射速度在10.35～53.5cm3／s范围变化，压力在21.2～63.6MPa变化。注塑温度和模具温度分别设定为185℃和40～60℃。分别在3个位置设定2个方向的浇口朝向，压力传感器和温度传感器安装在模具中，采集注塑过程中的熔体参数变化，并利用数据采集卡记录压力和温度数据，如图3所示。在不同成型参数下分别执行完整的注塑周期循环，测定模腔内的温度和压力变化数据。

图3 试验用的浇口、进浇方向和传感器布置

4 计算和试验结果分析

4.1 计算分析

为了获得包边过程中塑料和玻璃的温度分布，采用有限体积法［11－12］对（7）式进行求解。将包边模腔划分为一系列不重复的体积元，对（7）式每一个控制体积积分，得出一组离散方程。

为了考虑钢质模具对包边注塑过程的影响，引入系数w描述热传递的能力，理论上若w越小越趋于绝热，故在（4）式中添加含w项，即

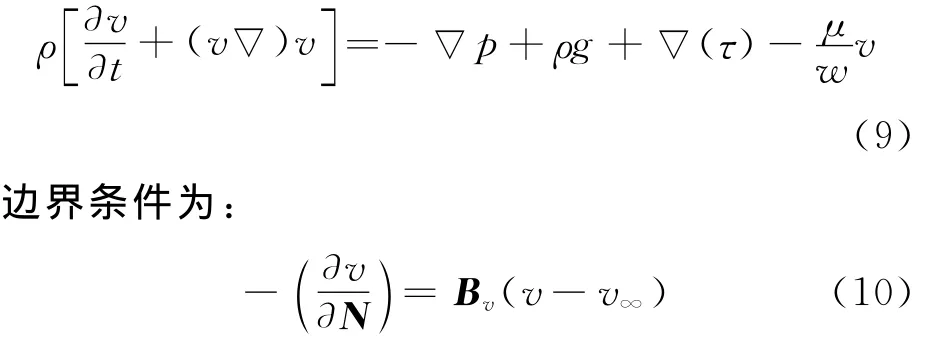
其中，Bv是速度向量（含3个坐标分量），则（9）式为：

对于能量方程，采用同样的步骤施加边界条件。在（7）式中引入数量值BT（T－T∞），得到如下能量方程：

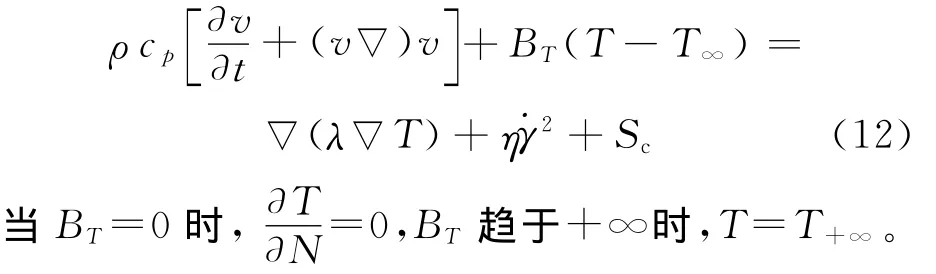
计算中，取熔体的流变参数如下［13］：n＝0.27，τ＊＝2310Pa，B＝3.04×10－9，β＝3.5×10－8Pa－1，熔化潜热 L＝3.33×105J／kg，θ0＝140℃，Δx＝8×10－4m，Δt＝0.2s，θf＝0℃。材料PVC的黏性模型中，k1＝1786Pa·s，k2＝0.054s，k3＝0.73（指数，无量纲），k4＝185℃，k5＝88℃。与传热相关的参数见表1所列［1，14］。

表1 PVC、模具钢和玻璃的相关参数

计算得到沿流道的一系列断面内指定时间的压力分布曲线，包边注塑的缝合线处是易出现撕裂强度不足的位置。当设定浇口位置1注射完成开始保压时，熔体缝合线处的压力分布如图4所示（单位为Pa）。由图4可见，玻璃嵌件的几何形状对压力分布的影响主要在接触边界上，使压力下降，从而对包边强度带来较大影响。此外，流道内熔体的黏性、注射压力、模腔的总容积对填充比例、浇口压力之间、缝合线处的压力影响也很大。当b增加时，填充体积和浇口压力降低，当b足够小时，可以使模腔压力达到最大比。

图4 熔接线断面处的熔体等压力线理论分布

计算得知，浇口位置由于改变了高分子流动的方向，它影响到填充时间和温度以及压力分布。浇口位置1处的填充比例、熔体剪切应力、熔接线的强度相对均匀，但压力衰减较严重。浇口位置3处的情况强度有所提高，但压力场的均匀性较差。浇口位置2的情况介于这两者之间。

4.2 试验结果和分析

利用设定的3个浇口位置1、2、3处，分别进行注塑试验。距离浇口在浇道总长度1／3处熔体的温度变化曲线，如图5所示。

距离浇口在浇道总长度2／3处熔体的温度变化曲线，如图6所示。距离浇口在浇道总长度1／2处，在横截面上流道处的温度变化曲线，如图7所示。

图5 距离浇道总长度1／3处熔体的温度变化

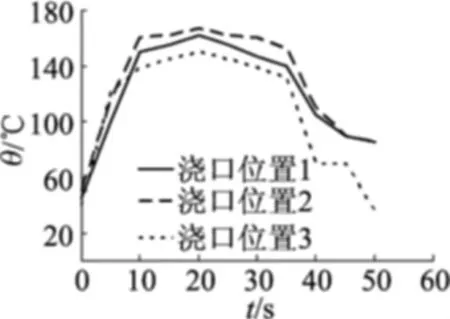
图6 距离浇道总长度2／3处熔体的温度变化

（1）温度波动在浇口位置附近最大，距离越远则有所减弱。其中，浇口位置1由于位于线性尺寸较大的边处，初始熔体成型过程中受到的阻力较小，温度波动较小，在注射和保压阶段约为18℃；位置2的流动过程不对称，且较早受到黏滞阻力，后续的成型温度变化较大，在注射和保压阶段约为26℃；位置3的情况则介于这两者之间。可以预测，采用浇口1时，沿流道方向上的包边效果要好一些，撕裂强度相对均匀。

（2）在同一断面处沿包边厚度方向上，采用浇口1温度变化剧烈，后2种方式则变化较平缓。原因在于沿流道方向流动黏滞阻力较小的情况下，沿包边厚度方向的成型有填充不足的趋势，压力下降梯度较大，反而使包边效果受到影响。

可以预测，此时的包边撕裂强度绝对值会有所下降。

图7 距离浇道总长度1／2处横截面上的温度变化

每种浇口形式注射出试样后，分别采集3个样品进行撕裂强度测试。在每个样品沿长度方向分别均匀地取3个测试点，结果见表2所列。由表2可见，撕裂强度情况与预测值基本一致。因此，浇口形式2既可以保障撕裂强度的均匀性，又能够保证撕裂强度的绝对值。

在生产中，针对形态千变万化的玻璃包边，设定浇口位置时，可以考虑位于曲率变化较大的位置附近，再根据包边断面的具体形态作综合分析。如果预设位置引起的黏滞阻力过大，则应避开此处一定的距离，以免引起包边撕裂强度不足。其次，玻璃的形态比较复杂时设定双浇口或多浇口，开设的部位要求既能够保障压力平衡，又能减小在注射和保压阶段的温度波动范围。还可以采用对称布置为一模双腔的形态，使注射过程趋于平衡。图8a所示为一个包边注塑模具应用实例，它的浇口既避开了包边断面变化剧烈的“尖角区”一定的距离，又保障了两腔的基本平衡。图8b所示为利用该模具生产出的包边玻璃。

表2 撕裂强度试验结果 N／mm

图8 玻璃包边注塑模具及产品

5 结 论

（1）根据玻璃包边塑件的几何和成型特点，建立包边注塑简化模型，该模型不受具体的玻璃型号和规格限制，对研究玻璃包边注塑工艺和模具具有一定的普适性。

（2）建立包括玻璃、模具、熔体的包边注塑的传递方程，设定了边界条件，用于定量计算包边注塑的能量和质量传递。

（3）利用数值计算方法得到沿流道的一系列断面内指定时间的压力分布曲线，分析了不同浇口位置对填充时间、温度、压力分布的影响。

（4）设定不同的浇口位置，测定距离浇口在浇道不同长度处和横截面上沿厚度方向上注塑熔体的温度变化曲线，分析温度变化和压力变化对包边效果的影响，分析包边注塑的浇口位置设置方法。

［1］Wang Qianting，Liu Qiong，Chen Wenzhe，et al.Gap distribution between fragile insert and mold in plastic boundary injection forming ［J］.Polymer－Plastics Technology and Engineering，2010，49（12）：1188－1195.

［2］林永南，刘 琼.基于最小功率损失的嵌件塑件注塑成形合模间隙分布［J］.合肥工业大学学报：自然科学版，2008，31（9）：1412－1414，1418.

［3］王乾廷，陈文哲，黄永华，等.汽车玻璃塑料包边注射成形中的传热建模与试验研究［J］.中国机械工程，2010，21（23）：2868—2871.

［4］Gatto A，Iuliano L.Evaluation of inserts for modular thermoplastic injection moulds produced by spin casting［J］.Journal of Materials Processing Technology，2001，118（1／2／3）：411－416.

［5］申明霞，蒋林华，费传军，等.芳纶纤维与表面处理层界面黏合机理研究［J］.橡胶工业，2007，54（8）：463－466.

［6］Schneider J，Kienzler A，Deuchert M，et al.Mechanical structuring，surface treatment and tribological characterization of steel mould inserts for micro powder injection moulding［J］.Microsystem Technologies，2008，14（12）：1797—1803.

［7］蒲启君.橡胶与骨架材料的黏合机理［J］.橡胶工业，1999，46（11）：683－695.

［8］Bird R B，Armstrong R C，Hassager O.Dynamics of polymeric liquids［M］.New York：John Wiley ＆Sons，1987：264－266.

［9］吴其晔，巫静安.高分子材料流变学［M］.北京：高等教育出版社，2002：263－264.

［10］Bird R B，Stewart W E，Lightfoot E N.Transport phenomena［M］.New York：John Wiley ＆ Sons，2007：89－93.

［11］王勖成.有限单元法［M］.北京：清华大学出版社，2003：689－691.

［12］Wu Zhixue.Stress concentration analyses of bi－material bonded joints without in－plane stress singularities［J］.International Journal of Mechanical Sciences，2008，50（4）：641—648.

［13］Osswald T A，Baur E，Brinkmann S，et al.International plastics handbook［M］.Munich：Carl Hanser Verlag，2006：560－565.

［14］Osswald T A，Turng L S，Gramann P J.Injection molding handbook［M］.Hanser：Cincinnati，2002：20－100.