基于Box-Cox变换的城市火灾起数的模型研究
2013-09-28谭常春周嘉章
谭常春, 张 诚, 周嘉章
(1.合肥工业大学 数学学院,安徽 合肥 230009;2.安徽省气象局 培训中心,安徽 合肥 230031)
火灾预测是火灾系统领域中一个关键的研究课题[1],而社会经济、技术、政治等因素都是影响城市火灾发生的重要外界因素,其中关于经济因素与火灾发生次数的关系研究比较多。
文献[2]研究得出经济水平的落后会导致火灾次数上升的结论;文献[3]认为收入与火灾起数之间有强烈的负向关系;文献[4]认为随着经济的发展,火灾形势是先严重后趋于缓和。
目前主要把火灾当作一门自然科学研究,偏重对客观环境、微观方面的研究[5]。气象因素对火灾发生、防治和损失控制方面有重要的影响[6]。文献[7]建立了气象因素与日本林火发生的广义线性预测模型[7];文献[8]从 Logistic和零膨胀Poisson(ZIP)回归模型方向,研究森林火灾与气象因素的关系。
统计分析,最常用的一般线性模型假定为:

其中,Y 为n×1的列向量;X=(xij)n×p为n×p的设计矩阵;β为p×1的未知参数向量;ε为随机误差。当ε服从正态分布时候,模型是最优的,但在实际应用中,常会遇到因变量分布不满足正态分布的情况,不能直接应用一般线性模型进行数据分析[9]。Box-Cox变换就是一种常用的非线性变换,通过确定一个最优的λ,将非正态数据变换成近似正态的数据[10],使变换后的数据比原有数据具有更好的线性性,再对变换后的数据进行回归分析[11]。
文献[6]直接对某市11a间的月度火灾发生起数与各气象因子建立线性回归模型,其拟合优度并不高。文献[12]通过对原始气象、火灾数据进行对数变换后建模,拟合优度虽然有所提高,但是并不特别理想。
本文应用Box-Cox非线性变换方法,先对原始数据进行适当Box-Cox变换,基于变换后的数据建立了回归模型,进行统计分析比较,并用于预测火灾发生趋势和起数。
1 方 法
1.1 Box-Cox变换
Box-Cox变换[10,13]是对变量y(y>0)进行变换,即
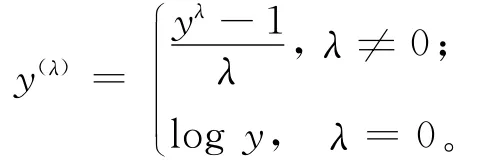
其中,y为原始数据。对于不同的λ,所作的变换也不同,常用变换有对数变换(λ=0)、平方根变换(λ=1/2)及倒数变换(λ=-1)等。
当误差分布呈现正偏态时,常对因变量进行对数变换;当误差分布呈现负偏态分布时,常采用平方根变换。为避免变量y≤0时无法进行变换的情形,可应用扩展的Box-Cox变换,即

此时的a是为了使y+a>0。
1.2 参数λ的估计方法
无论是基本式还是扩展式,真正需要估计的只有一个参数λ,为了确定一个最优的λ,将非正态的数据变换为近似正态的数据。
本文利用文献[13]提出的最大似然估计方法确定参数λ值,在规定范围内给出一系列的λ值。对固定的λ,令
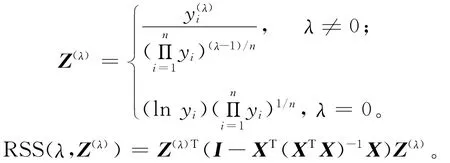
为了求ln Lmax(λ)的最大值,只需求残差平方和RSS(λ,Z(λ))的最小值。虽然很难找出RSS(λ,Z(λ))最小值点λ的显式解析式,但对一系列给定的λ值,通过线性回归模型的最小二乘估计,很容易计算出相应的 RSS(λ,Z(λ))值。画出 RSS(λ,Z(λ))关于λ的曲线,从图上可以近似地找出使RSS(λ,Z(λ))达到最小值的^λ。
1.3 Box-Cox变换步骤
(2)计算残差平方和 RSS(λ,Z(λ))。
(3)对一系列λ的值,以λ为横轴,RSS(λ,Z(λ))为纵轴,作出相应的曲线,用直观的方法,找出使 RSS(λ,Z(λ))达到最小值的点
1.4 数据预处理
本文仅对1997年及其以后的数据进行处理,其中1997—2003年某市火灾起数来自文献[14],2004—2006年某市火灾起数来自文献[15],按照当时的统计标准,火灾起数即为消防队出火警次数。2007年统计标准改变,仅将造成损失的火警数统计为火灾数据,为保持数据统计标准的连续性,本文选择某市消防局记录的月出火警次数作为2007年的火灾起数[14-15]。
首先对某市月火灾起数与各气象因子的原始数据进行Box-Cox变换,使变换后的数据具有更好的线性性,然后再进行相关分析和回归分析,其原始数据见表1所列。

表1 月火灾起数与各气象因子的原始数据
原始数据的火灾起数、风速、降雨量、温度、湿度依次记为freq、wind、rain、tempt、humi,原始数据摄氏温度常为负数,降雨量有部分值为0。选取Box-Cox变换的扩展公式,温度a1=273,降雨量a2=1。对火灾起数、风速、降雨量Box-Cox变换过程中λ值的选取,是根据最大似然估计方法确定的,火灾起数、风速、降雨量的λ值依次为-0.6334、0.286、0.1025。Box-Cox变换后的火灾起数、风速、降雨量依次记为bcfreq、bcwind、bcrain。但对温度和湿度,若继续采用最大似然估计方法选取λ,则发现Box-Cox变换后,温度数据非常大,湿度数据也偏大,故需要重新确定λ。为了使变换后的数据与其他气象因子变换后的数据在数值大小上相接近,多次选取λ对数据进行变换,最终确定温度和湿度的λ值为-0.5。记Box-Cox变换后的温度和湿度为bctemp、bchumi,各数据值计算如下:

此时变换后的温度和湿度因子数据与其他气象因子数据大小相接近,见表2所列。
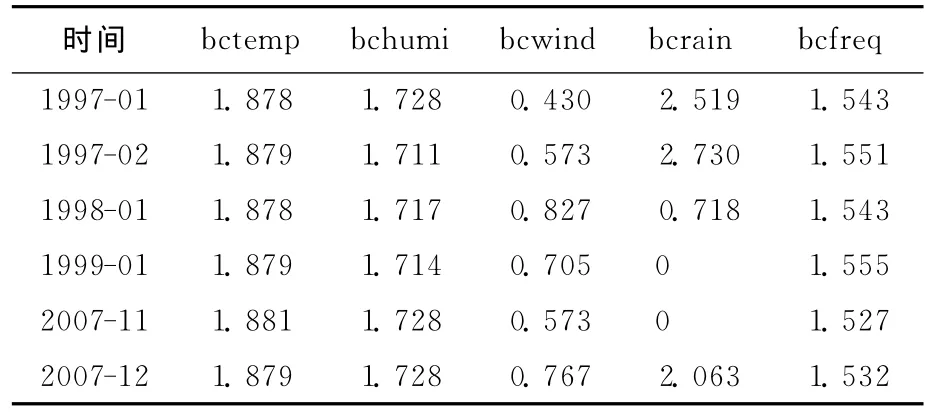
表2 Box-Cox变换后的火灾起数与各气象因子数据
2 回归模型建立
2.1 散点图分析
为了寻找火灾起数bcfreq与各要素之间的相关关系,研究火灾起数与各气象因子间是否存在线性趋势,通过绘制散点图来进行观察,如图1~图4所示。
从图1中的散点看出,bcfreq与bchumi具有明显的负相关关系。空气中水分含量较大时,火灾发生的次数相对较少。
从图2中的散点看出,bcfreq与bctemp成负相关,随着bctemp的增大,bcfreq反而减小,即随着温度升高,火灾发生起数下降。
从图3中的散点看出,bctemp与bcrain成负相关,随着降雨量的增大,火灾发生起数逐渐减少。
从图4中的散点看出,bcfreq与bcwind成一定的正相关,但相关性不大,即降雨量的变化对火灾发生起数的影响不大。
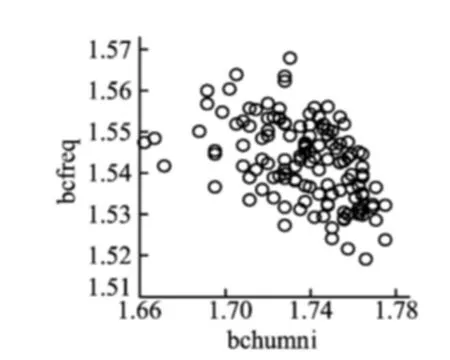
图1 bcfreq与bchumi的散点图

图2 bcfreq与bctemp的散点图
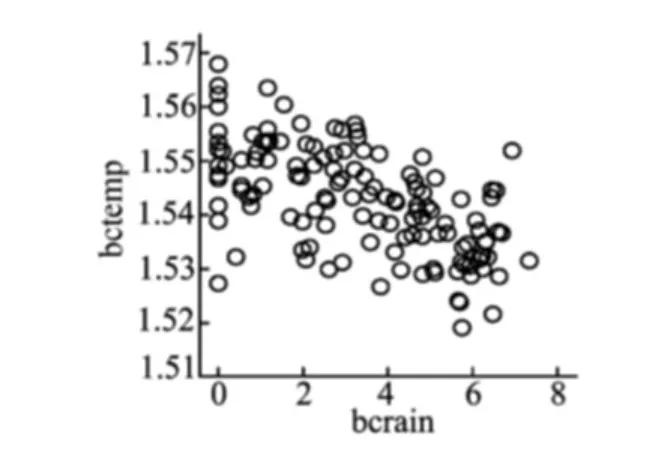
图3 bctemp与bcrain的散点图
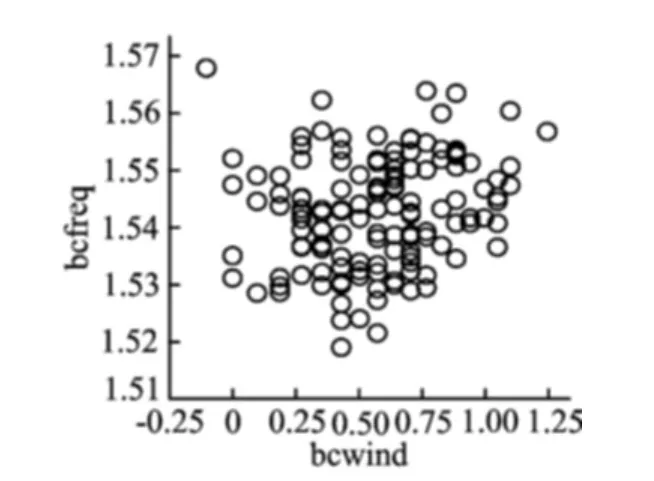
图4 bcfreq与bcwind的散点图
2.2 相关分析
从散点图大体了解气象各要素与bcfreq之间的相关程度,但需要知道各要素与bcfreq具体的相关性大小,因此需要计算bcfreq与各要素间的相关系数,结果见表3所列。

表3 线性相关系数
从表3可以看出,对月火灾发生起数的影响大小依次是bcfreq1、bcrain、bctemp、bcfreq2、bchumi、bcwind。
bcfreq1是最主要的影响因素,表明火灾上月发生起数对火灾发生起数影响最大,如果某月的火灾发生起数偏高,必然会引起相关部门的重视,从而采取相应措施。bcrain、bctemp、bcfreq2是次于bcfreq1的影响因素,bchumi对月火灾发生起数也有一定的影响,而bcwind与火灾发生起数的相关性不强,说明bcwind对火灾发生起数的直接影响不大,两者之间的相关性不强。bcrain、bctemp、bchumi均与bcfreq负相关,说明随着bcrain、bctemp、bchumi增大,bcfreq下降,即火灾发生起数下降;反之,bcrain、bctemp、bchumi越低,越容易发生火灾。
随着降雨量和空气湿度的增加,火灾发生起数会有所降低,这符合常识,但随着温度变高,月火灾发生起数不但没有增加反而减少,这似乎与常识不大符合,但注意到温度高的时节一般都伴随着强降雨,使空气湿度增加,反而降低了火灾发生的可能性。
2.3 回归模型建立
从各要素与火灾发生起数的相关性分析可知,bctemp、bchumi、bcwind、bcrain、bcfreq1对火灾发生起数都有一定的影响,以bcfreq为因变量,以bctemp、bchumi、bcwind、bcrain、bcfreq1为自变量,选择逐步回归法得到如下回归模型:

经Box-Cox变换后得到的回归分析模型(1)式的拟合度R2为0.730,比文献[6]未做变换时的拟合度0.543和文献[12]做对数变换的拟合度0.7053有较大的提高。
但发现建立逐步回归模型(1)式时,系统自动将bchumi、bcwind剔除,而从上述分析可知bchumi、bcwind对火灾起数有一定的影响,故将bchumi、bcwind强制加入模型中。
文献[12]未考虑到上月火灾起数对火灾起数的影响,通过火灾发生次数与气象因子的相关性分析,火灾发生起数与上月火灾发生起数也有较大的相关性,因此也尝试着将上月火灾发生起数放入到因变量中,进行回归分析。
建立以bcfreq为因变量,以bctemp、bchumi、bcwind、bcrain、bcfreq1、bcfreq2为自变量的强制回归模型如下:

本文发现,将bchumi、bcwind、bcfreq2强制加入模型中,模型的拟合度R2有一定提高,达到0.741,但可以看出Box-Cox变换后湿度的t检验P-value为0.361>0.05,未通过回归系数检验,因此尝试将bchumi剔除模型后,进行强制回归分析,再观察回归结果。
建立以bcfreq为因变量,以bctemp、bcrain、bcwind、bcfreq1、bcfreq2为自变量的强制回归模型如下:
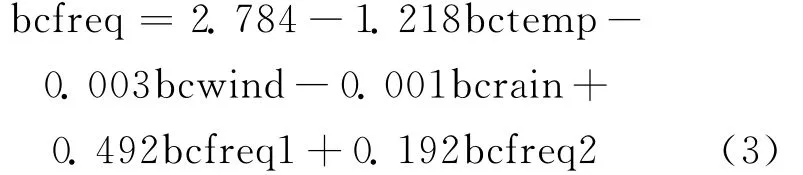
剔除bchumi后发现,模型的拟合度基本保持不变,但降雨量的回归系数也没有通过t检验,其P-value为0.064,但在0.1的显著性水平下,模型就全部通过了系数检验,因而确定模型3为最终预测模型。
3 模型评估
3.1 模型拟合图
采用最终选定的预测模型,对原始数据作拟合图,如图5所示,其中选定每年1月数据。
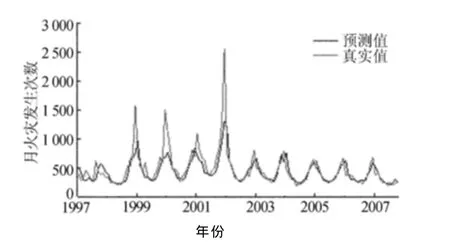
图5 预测模型拟合图
从图5可以看出,预测模型对原始数据的拟合效果较好,同时计算得到预测模型的相对均方误差为0.0537,说明预测模型比较理想。
3.2 交叉验证
交叉验证方法中常用的有K次交叉验证(K-flod Cross Validation),基本方法是将原始数据分成K组(一般是均分),将每个子集数据分别做一次验证集,其余的K-1组子集数据作为训练集,交叉验证K次,每组数据都被验证一次,然后计算预测均方误差,比较各个模型的预测均方误差,选择预测均方误差最小的拟合模型为选择模型。本文中K取13,得到预测模型交叉验证的均方误差为2.86×10-5,均方误差相对较小,预测模型比较理想。
3.3 模型预测与比较
采用2008年前7个月的火灾数据为数据检验集,将数据代入选定的预测模型中,得到月火灾起数的预测值,见表4所列,同时可以得到2008年前7个月火灾起数的预测值和实际值的对比,如图6所示。从图6可以看出,预测模型较准确地预测了2008年前7个月的火灾发生趋势,这7个月的火灾发生起数整体呈下降趋势,与实际值基本相符合,其中3月和5月预测值比实际值高,这可能是因为火灾起数的预测是一项较复杂的系统,受多重因素影响,而气象并非是影响火灾发生的唯一原因,仅采用气象因素预测火灾发生起数有一定的局限性。

表4 2008年1—7月火灾起数对比
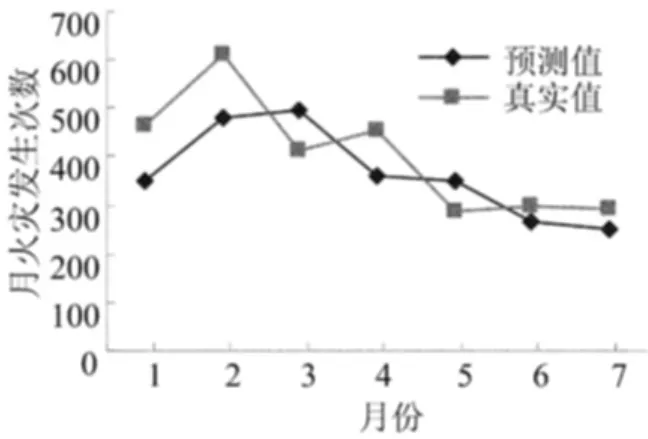
图6 2008年1—7月火灾发生起数对比
4 结束语
本文首先对火灾气象数据进行Box-Cox变换,然后对变换后的火灾气象数据进行回归分析,构造了3种基于Box-Cox变换后火灾起数与气象因子之间的回归模型,并通过分析比较,选定最终模型为预测模型,且所选定的回归预测模型能较好地反应和预测火灾发生的趋势和起数。结果表明,火灾气象因子中平均温度、平均相对湿度以及平均降雨量对火灾起数影响显著,而风速对火灾起数的影响不大。Box-Cox变换是将非线性的数据变换成线性数据的有效方法,Box-Cox变换后所建立的回归方程能更好地预测火灾发生次数,从而达到对城市火灾控制的目的。
[1]楚志勇.基于回归分析方法的城市火灾预测[J].安全与环境工程,2011,18(3):90-97.
[2]Philip S.Procedures for improving the measurement of local fire protection effectiveness[M].Boston:National Fire Protection Association,1977:53-71.
[3]Gunther P.Fire-cause patterns for different socioeconomic neighborhoods in Toledo[J].Fire Journal,1981,75:52-58.
[4]杨立中,江大白.中国火灾与社会经济因素的关系[J].气象,1993,19(7):47-51.
[5]吴卢荣,马咏真,陈绩馨,等.中国火灾与社会经济因素的相关分析[J].中国安全科学学报,2007,17(6):92-97.
[6]刘 宁,祝国苓.火灾与气象因素的相关性研究[J].武警学院学报,2010,26(2):22-25.
[7]田应福,金百锁,缪柏其,等.日本林火的广义线性模型[J].统计与决策,2006(14):49-52.
[8]缪柏其,韦 剑,宋卫国,等.林火数据的Logistic和零膨胀Poisson(ZIP)回归模型[J].火灾科学,2008,17(3):143-149.
[9]李运明.Box-Cox变换及其在SPSS软件中的实现[J].数理医药学杂志,2009,22(5):569-571.
[10]王 欢,袁永生.Box-Cox变换用于分位数回归曲线相交问题的研究[J].数理统计与管理,2009,28(6):1024-1029.
[11]胡宏昌,樊献花.广义 Box-Cox变换[J].周口师范学院学报,2006,23(5):17-19.
[12]谭常春,周 尧.城市火灾次数与气象因素的回归模型[J].统计与决策,2011(18):31-33.
[13]王松桂.线性统计模型[M].北京:高等教育出版社,1999.
[14]公安部消防局.中国火灾统计年鉴(1997—2003)[M].北京:中国人民公安大学出版社,1997—2003.
[15]公安部消防局.中国消防年鉴(2004—2006)[M].北京:中国人事出版社,2004—2006.
