卫星导航信号异常对信噪比的影响

刘建成 ,桑怀胜,徐 贝,冯晓超

(北京卫星导航中心,北京 100094)

1 引 言

自GPS SV19号卫星被发现信号异常以来,卫星导航信号质量问题受到越来越多的重视[1-4]。造成卫星导航信号异常的卫星故障可分为三类,即数字电路故障、模拟电路故障或者两者的混合。数字电路故障只与导航卫星有效载荷的数字单元有关,模拟电路故障只与导航卫星有效载荷的模拟单元有关,而混合故障与数字单元和模拟单元均有关,即同时发生数字电路故障和模拟电路故障[5]。2OS(Second-Order Step)模型是国际民航组织认可的卫星导航异常信号模型[6]。把数字电路故障、模拟电路故障和混合电路故障引起的异常信号模型分别称为TMA(Threat Model A)、TMB(Threat Model B)和 TMC(Threat Model C),由超前/滞后参数、振荡频率和衰减因子等3个可变参数来定义[5,7]。

近年来,对卫星导航信号畸变波形检测方面的研究越来越多[1-2,5]。文献[1]采用了功率谱分析、码片边缘分析、眼图、星座图、相关峰曲线与相关损耗等多种分析方法研究了导航卫星的空间信号进行质量分析。文献[2]提出了星上自主导航有害波形检测方法。文献[5]研究了2OS模型相关输出的非对称性,并利用多相关器技术进行异常波形检测。由于信噪比是导航接收机输出的一个重要变量,且与文献[1]的相关损耗分析方法有一定联系,因此需要研究卫星导航信号异常对信噪比的影响并分析是否能作为信号异常检测的手段。

根据2OS模型的3种类型,分别研究其相关峰特性,这是分析对信噪比影响的基础。根据典型导航接收机特性,推导异常导航信号信噪比相对正常导航信号信噪比的差异,以获得3种异常信号模型分别对信噪比的影响程度。由理论分析结果,在2OS模型参数取值范围内进行数值分析,并根据数值分析结果,判断信噪比是否能作为信号异常检测手段。

2 卫星导航异常信号模型

正常的卫星导航信号伪随机码波形定义为

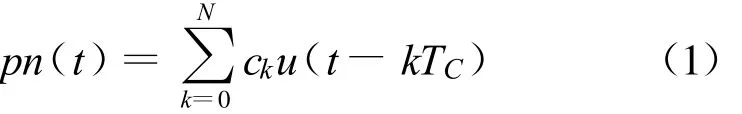
式中,ck为二进制伪随机码,u(t)为单位幅度矩形脉冲,TC为伪码码元宽度,N为码元个数。

异常信号TMA模型用伪随机码码片的下降沿超前或滞后来实现数字电路故障的建模[5]。该模型只有一个可变参数,即超前/滞后参数Δ,表示伪随机码码元的下降沿超前或滞后多少,其参数变化范围是[5]-0.12≤Δ≤0.12。

异常信号TMB模型用衰减二阶响应作为对模拟电路故障的建模[5]:

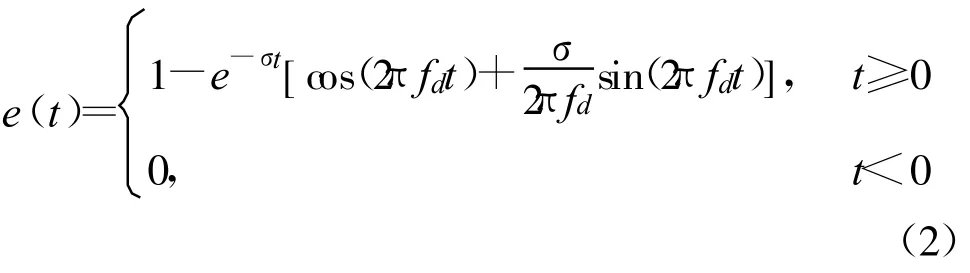
该模型包括两个可变参数,即振荡频率fd和衰减因子σ,其中振荡频率表示振荡的快慢,衰减因子表示振荡幅度衰减的大小,其参数变化范围是[5]7.3 MHz≤fd≤13 MHz,0.8 MNp/s≤σ≤8.8 MNp/s。

异常信号TMC模型是TMA模型和TMB模型的综合,可以实现对混合故障的建模。该模型包括3个可变参数,即超前/滞后参数Δ、震荡频率fd和衰减因子σ,其变化范围同上。

3 卫星导航异常信号相关峰特性

3.1 理想相关峰

忽略伪随机码旁瓣的影响,只考虑相关峰部分,此时卫星导航信号的相关峰可表示为

式中,TC为伪码码元宽度,TC=1/fc,fc为伪码速率。

正常导航信号相关峰以 τ=0为中心左右对称,且最大值位于中心位置。

3.2 TMA模型异常相关峰

考虑滞后情况,TMA模型相关峰可表示为

式中,TC为伪随机码码元宽度,Δ为滞后码元宽度比例。

3.3 TMB模型异常相关峰

[5]的做法,利用卷积性质,TMB模型的相关峰可表示为

式中,e(α)由式(2)确定,Rnom(τ)由式(3)确定。

令

则

分别对伪码速率为1.023MHz、2.046 MHz、10.23MHz的情况,在可变的TMB模型参数范围内进行数值分析,结果表明:TMB模型相关峰呈现非对称性,在τ=0附近有一个最大值,在很大的参数范围内,该最大值大于1。

3.4 TMC模型异常相关峰

采用与导出TMB模型相关峰相同的方法,可得到TMC模型相关峰为

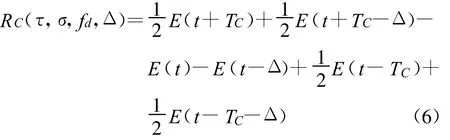
分别对伪码速率为1.023 MHz、2.046 MHz、10.23 MHz的情况,在可变的TMC模型参数范围内进行数值分析,结果表明:TMC模型相关峰同样呈现非对称性,且有一个最大值,最大值及其位置与TMC模型的3个可变参数有关。

4 卫星导航信号异常对信噪比的影响

下面首先理论推导得到卫星导航异常信号信噪比与正常卫星导航信号信噪比之差,然后在典型参数情况下进行数值分析。

4.1 异常导航信号的信噪比

不失一般性,忽略导航数据信息的GNSS接收机接收信号模型为

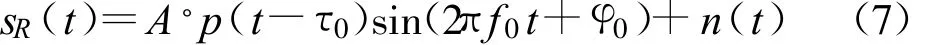
式中,A为接收信号幅度,p为导航卫星下播的伪码,τ0为传播时延,φ0为相位,f0为中心频率,n(t)为接收机噪声。

GNSS接收机I、Q支路本地复制信号分别表示为

式中,τ0、φ0、f0分别为传播时延 、相位和中心频率的估计值。

中心频率估计误差忽略不计,经GNSS接收机处理后,I、Q支路相关器的信号输出分别为

由此可得GNSS接收机信号功率

那么GNSS接收机输出信噪比为

式中,A为接收信号幅度,N0为相关器后的噪声功率,Rmax为相关峰的最大值。

根据上式可得到TMA、TMB和TMC 3种模型下异常导航信号信噪比与正常导航信号信噪比之差为

式中,RAmax、RBmax、RCmax分别为TMA 模型 、TMB 模型和TMC模型相关峰的最大值。

4.2 数值分析

下面的数值分析考虑了3种伪码速率,分别为1.023MHz、2.046 MHz、10.23 MHz。假设不同的伪码速率2OS模型参数范围相同,针对每种伪码速率,分别数值分析在模型参数可变范围内信噪比所能改变的最大值。

4.2.1 TMA模型异常信号的信噪比

TMA模型异常信号信噪比与正常信号信噪比之差如图1所示。显然,TMA模型信噪比改变与伪码速率无关。在TMA模型参数变化范围内,TMA模型信噪比最大损失0.5374 dB。

图1 TMA模型异常信号信噪比损失大小与Δ的关系Fig.1 Relationship between SNR loss and Δfor TMA

4.2.2 TMB模型异常信号的信噪比

TMB模型异常信号信噪比与正常信号信噪比之差如图 2所示。伪码速率为1.023 MHz、2.046MHz、10.23MHz时的信噪比最大增加分别为0.2586 dB、0.6036 dB、3.2928 dB。由此可见,伪码速率越高,TMB模型信号异常对信噪比的贡献越大。但伪码速率为10.23MHz时,在 σ较小且fd在11 MHz附近,信噪比不是增加而是损失,最大损失0.3219 dB。

图2 TMB模型异常信号信噪比增加量与σ及fd的关系Fig.2 Relationship between SNR increasment,σand fdfor TMB

4.2.3 TMC模型异常信号的信噪比

固定Δ=0.1,TMC模型异常信号信噪比与正常信号信噪比之差如图3所示。伪码速率为2.046 MHz、10.23 MHz时信噪比最大增加分别为0.2777 dB、3.2317 dB。与TMB模型相比,信噪比最大增加相对减少了,这是由滞后Δ=0.1导致的。

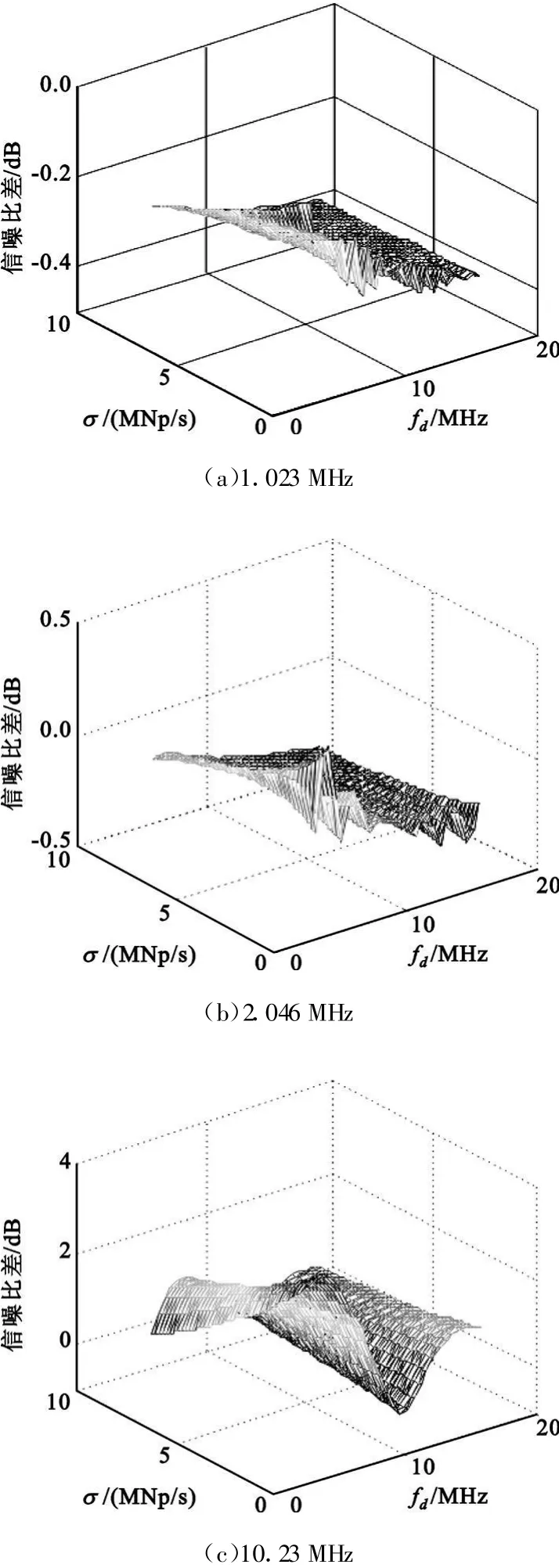
图3 TMC模型异常信号信噪比增加与σ及fd的关系Fig.3 Relationship between SNR increasment,σand fdfor TMC

5 结 论

根据卫星导航异常信号的3个2OS模型,即TMA、TMB和TMC,分析了其相关峰特性,然后推导得到了3个模型下异常导航信号信噪比与正常信号信噪比之差,并在模型参数取值范围内分别进行了数值分析。结果表明,TMA模型信号异常会造成信噪比损失,而TMB和TMC模型信号异常在某些情况下对信噪比有增强作用,因此信噪比不能作为2OS模型卫星导航信号异常的监测手段。

参考文献:

[1]卢晓春,周鸿伟.GNSS空间信号质量分析方法研究[J].中国科学:物理学力学天文学,2010,40(5):528-533.LU Xiao-chun,ZHOU Hong-wei.Methods of Analysis for GNSS Signal Quality[J].Scientia Sinica Phys,Mech&Astron,2010,40(5):528-533.(in Chinese)

[2]王斌,庞岩,刘会杰.导航信号有害波形检测技术研究[J].电子与信息学报,2011,33(7):1713-1717.WANG Bin,PANG Yan,LIU Hui-jie.Research of Detection Technique of Navigation Signal′s Evil Waveform[J].Journal of Electronics&Information Technology,2011,33(7):1713-1717.(in Chinese)

[3]Macabiau C,Chatre E.Impact of evil waveform on GBAS performance[C]//Proceedings of the IEEE PLANS 2000.SanDiego California:IEEE,2000:22-29.

[4]Wong G,Phelts R E,Walter T,et al.Bounding ErrorsCaused by Nominal GNSS Signal Deformations[C]//Proceedings of the ION GNSS.Manassas,V A:ION,2011:2657-2664.

[5]Phelts R E.Multicorrelator techniquesfor robustmitigation of threats to GPS signal quality[D].California:Stanford University,2001.

[6]Mitelman A M.Signal quality monitoring for GPS augmentation systems[D].California:Stanford University,2004.

[7]Phelts R E,Walter T,Enge P.Characterizing nominal analog signal deformation on GNSS signals[C]//Proceedings of the 2009 ION GNSS.Savannah,GA:ION,2009:1343-1350.