基于奇异值分解的多卫星信号盲检测
2013-09-28张立民钟兆根
张立民,钟兆根, ,彭 耿
(1.海军航空工程学院 电子信息工程系,山东 烟台 264001;2.海军装备研究院,北京102249)
1 引 言
为了获取详细的敌方卫星通信链路情报信息,进而实施有效的干扰,其前提是对接收到的混合信号进行有效检测。针对现有复杂多变的卫星信号环境特点,如何实现非合作低信噪比条件下卫星信号的快速盲检测,是现阶段急需解决的问题。
目前,国内外学者就这一问题已经提出了许多行之有效的方法[1-2],但这些方法大都需要利用信号的某些先验知识,不是严格意义上的盲检测。针对像能量法、功率谱法等传统盲信号检测方法不能适应低信噪比等缺陷,文献[3-5]提出了一些针对性较强的方法,它们在一定程度上能提高信号的检测性能,但也存在着适应信号类型单一、计算复杂和不能适应多信号环境等缺陷。为了更好地解决这一问题,文献[6]在前人研究的基础上,提出了一种快速盲信号检测方法,虽然该方法能满足现实设备的需求,但是要应用在卫星等高速运行的环境下,该方法计算量还是相对较高。为此,本文改进了该方法的实现步骤,并从理论上给出了算法的检测性能分析,进一步验证了算法的可行性,并减少了计算量。
由于通常采用的无线电侦察接收机都是宽开的,多个信号可能同时进入到接收机。本文在对上述方法进行充分分析的基础上,根据观测矩阵奇异值与自协方差矩阵特征值之间的关系,提出了一种基于奇异值分解的多卫星信号快速盲检测方法,仿真结果验证了该方法对低信噪比、多信号环境的适应性。同时,该方法的计算量相对特征值方法大大减少,更适合应用在星载设备上。
2 检测算法的提出
本节在建立的信号模型基础上,给出一种基于奇异值分解的盲检测算法。
2.1 接收信号模型
针对现有的复杂电磁环境,卫星侦察接收机的离散观测信号可表示为
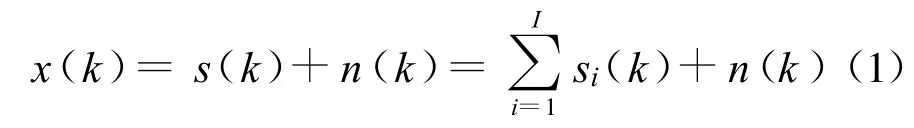
式中,I≥0为信号个数;n(k)是零均值、方差为σ2的加性高斯白噪声;si(k)为第i个数字调制卫星信号,且认为各信号间、信号与噪声间都是不相关的。
假设离散采样之后的观测数据x(k)含有N个采样点,即 k=1,2,3,…,N。为描述方便,首先对数据进行零均值化处理,然后可利用重叠分段的方法,把长度为N的观测数据分成N-M+1个相互重叠、长度为M、重叠长度为M-1的信号片段,为不失一般性,可令N-M+1≥M,将分段得到的数据写成如下M×(N-M+1)维的Hankel矩阵形式:
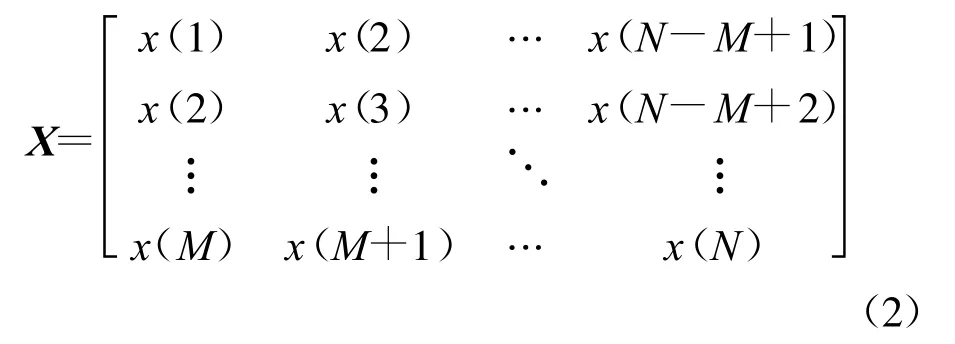
则信号检测问题可转化为如下二元假设检验:

式中,P为检测统计量,T1为检测门限。
2.2 检测量的设计
针对上述接收信号模型,在奇异值分解定理的基础上,对观测矩阵做如下分解:

其中,U和V为酉矩阵,VH为 V的共轭转置,Δ为准对角矩阵:

式中 ,D=diag(α1,α2,α3,…,αM),对角元素为 X 的非零奇异值 ,且 α1≥α2≥α3≥…≥αM>0。
下面给出观测矩阵奇异值与自协方差矩阵特征值的关系,首先定义自协方差矩阵为

式中,符号 E{·}表示期望。将式(4)代入式(6)可求得RX的特征值分解为

式中,□=ΔΔH也为对角矩阵,其对角元素为 RX的特征值,于是可知观测矩阵的奇异值与自协方差矩阵的特征值是平方关系,RX的特征值为α2i,1≤i≤M。同时,由式(1)和式(6)可知:
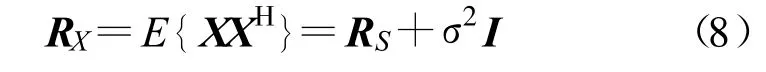
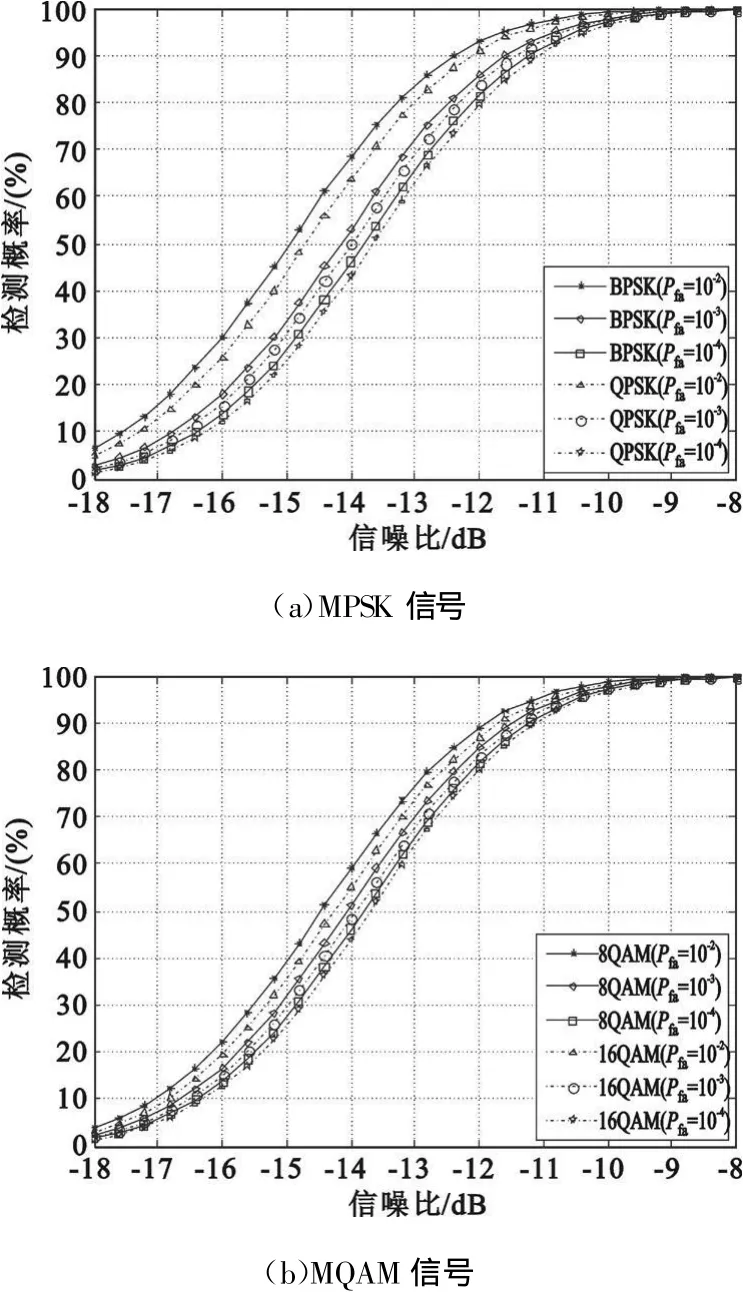
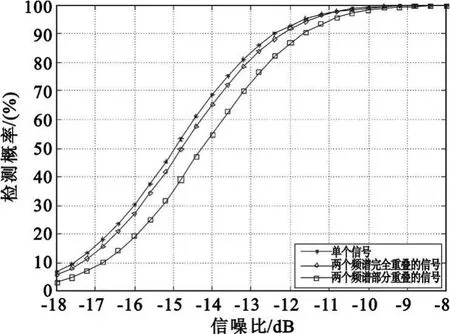
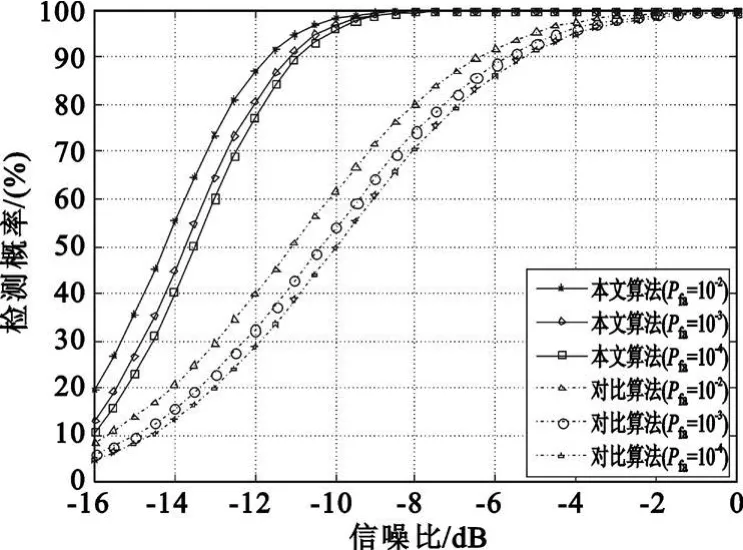
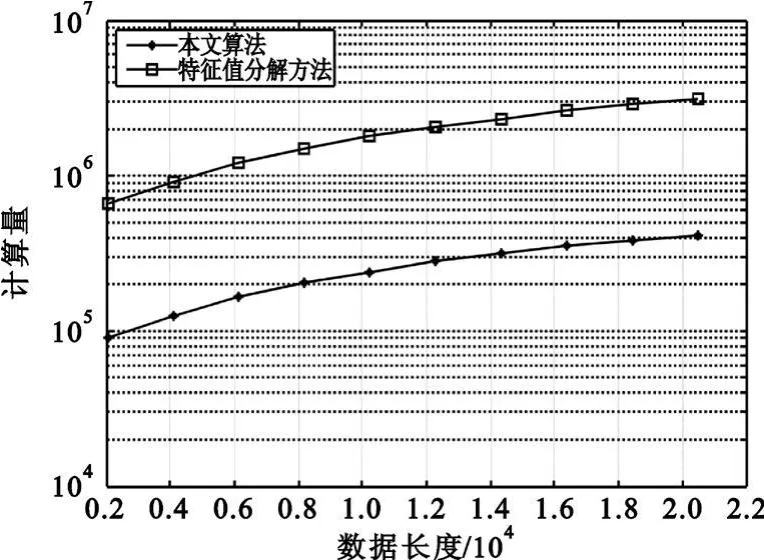
式中,RS为信号的自协方差矩阵,I为M阶单位矩阵,且RS为半正定的Hermitian矩阵,假设其秩为D(D 式中,Λ为D阶对角矩阵,其主对角线元素为RS的非零特征值(设为 λi(i=1,2,3,…,D),且按降序排列)。将该式代入式(8)可得RX的特征值为 根据阵列信号处理的相关定义可知,D个较大特征值对应的特征向量张成空间称为信号子空间,M-D个较小特征值对应的特征向量张成空间称为噪声子空间,且信号子空间与噪声子空间正交。 在前期的研究工作中,文献[7]通过估计信号子空间的维数大小来判断信号的有无,但是在低信噪比条件下,这种维数估计的方法可靠性不强,一旦估计错误整个算法就可能会失效。针对这一问题,本文采用文献[6]设计的类似检测统计量,通过理论分析并推导检测算法的性能,使得其检测性能不受空间维数估计的影响,即 式中,E为待估计的信号子空间维数。 对于上面建立的检测统计量,首先需要估计出信号子空间的维数E,然后通过推导得出检测量的统计特性,进而确定检测门限。 信号子空间的估计方法在阵列信号处理中已比较成熟,如基于信息论准则的方法和盖氏圆准则的方法等。本文采用文献[8]给出的MDL方法来估计子空间维数E,不同的是,文中不再用特征值判决函数进行计算,而是采用奇异值进行处理,这种替换在文献[9]中已得到了证明: 已被Anderson等[10]证明,对实自协方差矩阵有 式中,N(0,1)表示标准正态分布。对上式进行变换,化为检测量P的表达式,可得 于是在H0成立时,μ0=E(P H0),通过给定的虚警概率Pfa就可以得到检测门限gT,从而得出绝对检测门限 T1=μ0+gT·σ1。 针对噪声的随机性而导致的信号漏检问题,本文通过做重复实验来有效抑制信号漏检,给出一种平均符号检测方法:首先对上述的检测量做100次重复实验,分别为 Pi、T1i(i=1,2,3,…,100),则这100个值大于绝对门限的百分比为 式中,sgn为符号函数,最后给出置信概率门限 T2(本文选取为80%),当 TRatio大于T2时,则以大概率相信有信号存在,否则就没有信号。 下面给出盲信号检测算法的实现步骤: (1)首先对观测信号进行零均值化处理,按照式(2)给出的方式进行分段处理,得出观测矩阵 X; (2)对观测矩阵进行奇异值分解,求出非零的奇异值 αi(α1≥α2≥α3≥…≥αM>0); (3)采用式(12)~(13)的判决方法估计E; (4)由E结合式(16)~(17)计算检测量的均值和方差,进而根据 Pfa确定T1; (5)根据式(11)计算检测量P; (6)重复步骤2~5做100次仿真实验,根据式(18)计算平均符号概率TRatio; (7)若TRatio大于检测置信概率 T2则相信有信号存在,否则就没有信号。 本节首先从理论上分析算法的检测性能,根据检测量与信噪比的关系得出本算法所能适应的最低信噪比,然后对比算法的计算量。 由式(16)可知: 根据纽曼皮尔逊准则,在给定虚警概率Pfa,可求出检测门限T1,从而可得出检测概率如下: 综合式(19)对上式化简可得 下面给出检测量与信噪比的关系,进而得出本算法所能适应的最低信噪比。由文献[11]可知,信噪比与观测矩阵的奇异值满足如下关系: 将式(11)代入上式整理得 若单次检测到信号,则P大于T1,即 从上面的式子可以看出,在给定虚警概率的条件下,单次检测所能适应的最低信噪比可表述为 令M=10、N从1000到9000,单次检测所能适应的最低信噪比如图1所示。 图1 不同条件下单次检测所能适应的最低信噪比Fig.1 The minimum SNR that a single detection can adapt 由该图可知:仿真值与理论值之间虽存在一定的差异,但趋势是基本吻合的,它们之间存在的差异主要是由奇异值的估计误差等因素造成的。 由前面的分析可见,奇异值分解方法与文献[6]给出的方法都可分为4步来计算:第一是生成观测矩阵或协方差矩阵;第二是估计奇异值和特征值;第三是子空间维数估计;第四是检测比较分析。下面主要讨论比较两种方法的计算量,并假设加法、乘法和比较运算的计算量相当,其结果如表1所示。 表1 计算量分析Table 1 Computational complexity analysis 本节首先就单个和多个信号时算法的检测性能进行仿真验证,然后将本文方法与典型盲检测算法进行性能对比,同时给出计算复杂度对比结果。 (1)仿真实验1:验证算法对单个信号的检测性能 本次仿真实验分别验证算法对MPSK、MQAM信号的检测性能,其参数设置为:N=5000,M=50,Pfa分别为 10-2、10-3、10-4,T2为 80%,采样频率200MHz,信号载频70 MHz,码元速率10Mb/s,扩频码长1023,进行10000次Monte Carlo仿真,其结果如图2所示。 图2 不同虚警概率时单个信号的盲检测仿真结果Fig.2 Simulation results for different probability of false alarm 由图 2可知:在 Pfa小于 10-2、SNR=-11 dB时,MPSK、MQAM常用卫星信号的检测概率均达到90%以上,能较好满足信号侦察的需求。 (2)仿真实验2:验证算法对多个信号的检测性能 在Pfa为10-2、T2为80%、其他仿真参数同实验1,两个信号混合的功率比为0 dB,频谱重叠度分别为50%、100%。SNR为信号能量与噪声能量比值的对数,Monte Carlo仿真10000次,其结果如图3所示。 图3 信号个数、频谱重叠度对算法性能的影响Fig.3 The influence of signal number and spectrum overlap 由图3可知:信号个数、频谱重叠度虽对算法性能有一定影响,但影响不大,究其原因是检测量 P在多个信号情况下能将每个信号能量累加起来进行考虑,即更充分地将信号能量集中起来利用。 (3)仿真实验3:与典型算法的性能对比 文献[12]提出了一种较典型的DSSS信号盲检测算法,选取其作为对比算法,仿真参数同实验1,Monte Carlo仿真10000次,其结果如图4所示。 图4 检测性能对比曲线Fig.4 The comparison curve of detection performance 由图4可知:相对于文献[12](虚警概率为1%、SNR=-10 dB时,检测概率可达50%以上),本文算法的性能有明显提高,且适应的信号类型不仅局限于DSSS信号,检测性能的提高在于检测量 P能将信号的能量有效集中起来利用。同时,将本文的仿真结果与文献[6]的仿真结果比较可知,两者的性能差不多,但本文是在对检测量进行理论分析的基础上得出的结论,其仿真结果更具备可靠性。 针对表1的计算量分析结果,令数据长度N从2048变化到20480时,可得图5所示的计算复杂度对比曲线。由图可知:相对于特征值分解的盲检测算法,本文的计算量一般为其1/10,具有相对较小的计算复杂度,更适合应用在实时性要求较高的星载设备上。 图5 与文献算法的计算复杂度对比Fig.5 The comparison of computational complexity 针对日益复杂时变的多卫星信号侦察环境,本文在分析、研究当前通信信号盲检测方法的基础上,根据观测信号奇异值与协方差矩阵特征值之间的关系,提出了基于奇异值分解的多卫星信号快速盲检测算法,并从理论上推导了检测算法的检测性能,给出了检测量与信噪比的关系。从计算复杂度的对比分析可知,相比于文献[6]的特征值方法,本文方法确实能在很大程度上减少计算量,并达到快速实时的效果。仿真结果表明,算法的性能有明显提高,且适应的信号类型不仅局限于直扩信号,相比于功率谱和能量检测等传统方法,该算法能将多个信号的能量集中起来进行考虑,因此在多信号检测时能适应更低的信噪比。这为星载侦察设备的研制和空间信息对抗技术的研究提供了重要的技术支持,具有重要的意义。 [1]Barkat M.Signal detection and estimation[M].2nd ed.Norwood,MA,USA:Artech House,2005. [2]HillD A,Bodie J B.Carrier detection of PSK signals[J].IEEE Transactions on Communications,2001,49(3):487-496. [3]Cheng X,Vanhaverbeke F,Guan Y L.Blind combining for weighted energy detectuin of UWB signals[J].Electronics Letters,2011,47(1):55-57. [4]Tsung Hui Chang,ChienWei Hsin,Wing Kin Ma,et al.A linear farctional semidefinite relaxation approach to maximumlikelihood detection of higher-order QAM OSTBC in unknown channels[J].IEEE Transactions on Signal Processing,2010,58(4):2315-2326. [5]BarbieriA.Blind Per-State detection of DPSK over correlated fading channels[J].IEEE Transactions on Vehicular Technology,2010,59(5):2320-2327. [6]彭耿,黄知涛,陆凤波,等.基于特征值分析的通信信号快速盲检测方法[J].电子学报,2009,37(9):1950-1958.PENG Geng,HUANG Zhi-tao,LU Feng-bo,et al.A fast blind detection algorithm of communication signals based on eigenvalue analysis[J].Acta Electronica Sinica,2009,37(9):1950-1958.(in Chinese) [7]沙志超,彭耿,徐神,等.基于信号子空间维数估计的单通道盲信号检测[J].信号处理,2009,25(8A):94-97.SHA Zhi-chao,PENG Geng,XU Shen,et al.Single channel blind signal detection based on signal subspace dimension estimation[J].Signal Processing,2009,25(8A):94-97.(in Chinese) [8]Jensen J,Heusdens R.Improved subspace-based singlechannel speech enhancement using generalized super-Gaussian priors[J].IEEE Transactions on Audio,Speech,and Language Processing,2007,15(3):862-872. [9]刘玲,曾孝平,曾浩.基于奇异值的信源数估计方法[J].计算机工程,2009,35(12):34-37.LIU Ling,ZENG Xiao-ping,ZENG Hao.Signal source number estimation method based on singular value[J].Computer Engineering,2009,35(12):34-37.(in Chinese) [10]Anderson T W.An introduction to multivariate statistical analysis[M].New York:Wiley,1958. [11]詹亚锋,曹志刚,马正新.无线数字通信的盲信噪比估计[J].清华大学学报(自然科学版),2003,43(7):957-960.ZHAN Ya-feng,CAO Zhi-gang,MA Zheng-xin.Blind SNR estimations inwireless digital communications[J].Journalof Tsinghua University(Science and Technology),2003,43(7):957-960.(in Chinese) [12]BurelG,Bouder C,Berder O.Detection of direct sequence spreadspectrum transmissionswithout prior knowledge[C]//Proceedings of 2001 IEEE Global Telecommunications Conference.San Antonio,USA:IEEE,2001:236-239.
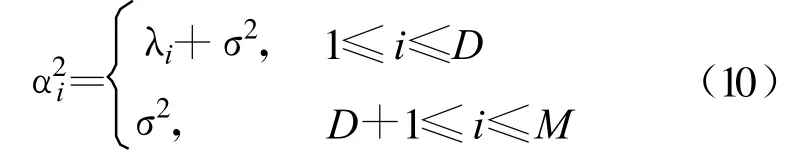
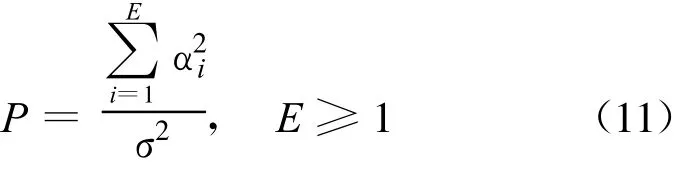
2.3 门限等参数的确定
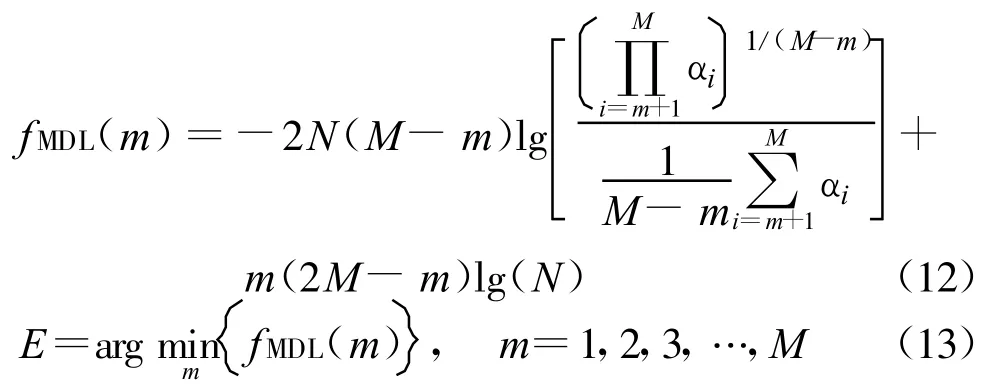
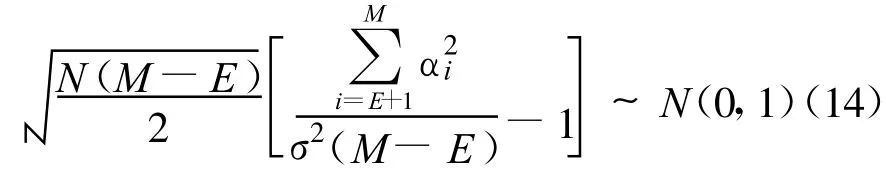
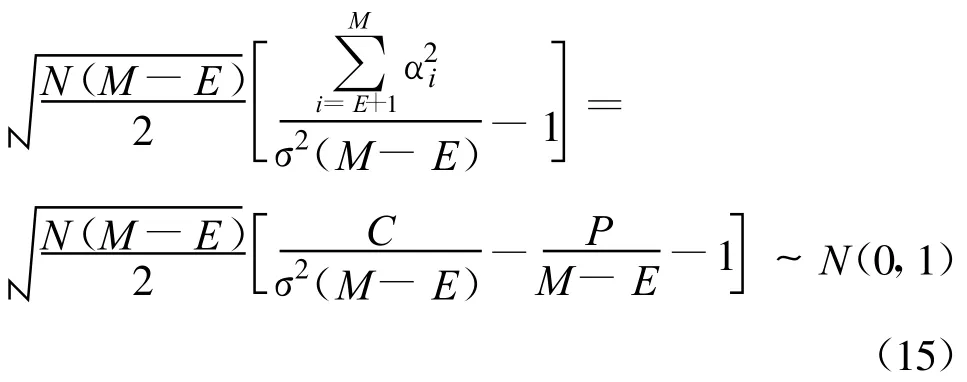
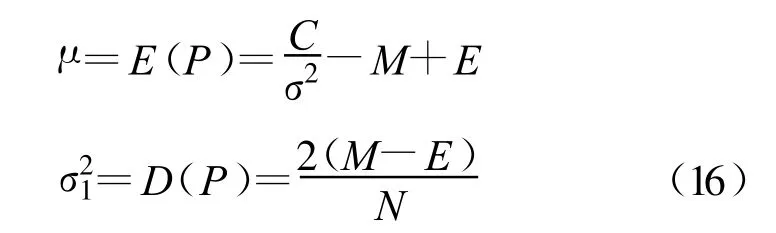


2.4 算法描述
3 检测性能和计算量分析
3.1 检测性能分析
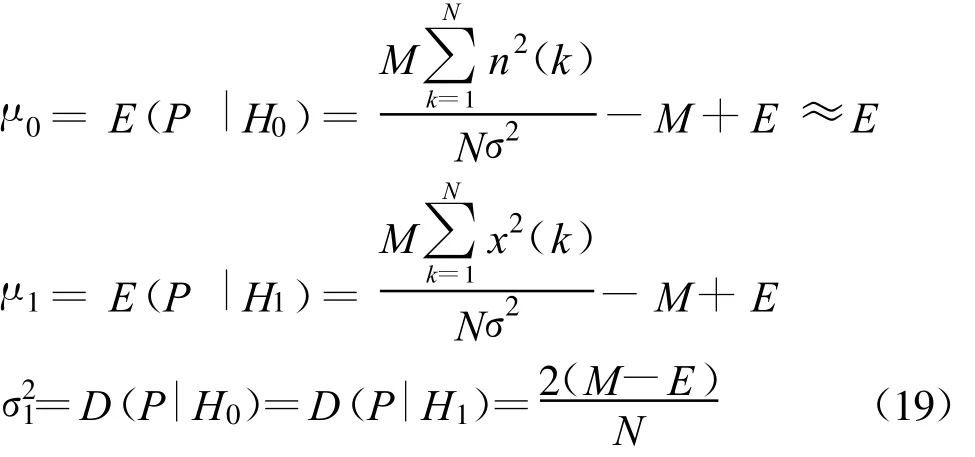
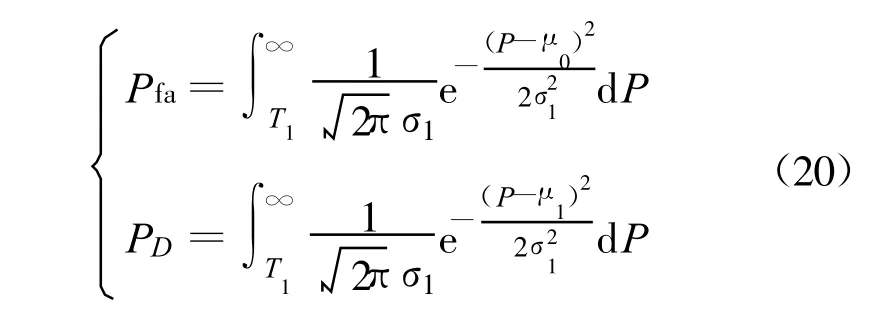
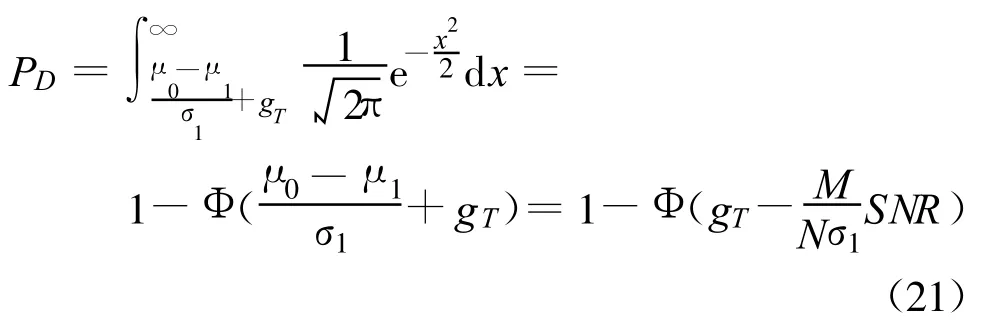
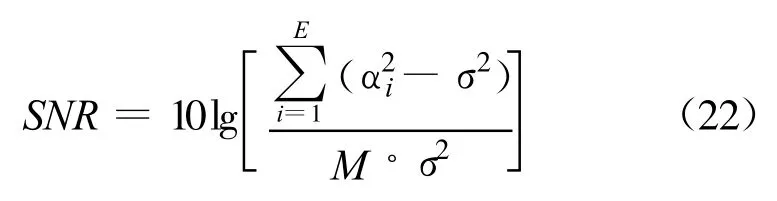


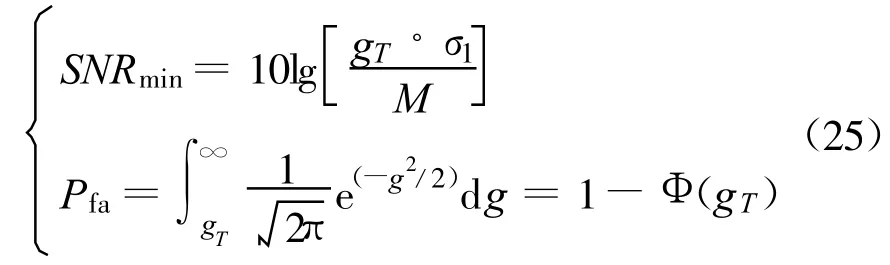

3.2 计算量分析

4 仿真实验
5 结 论
