双任务条件下青少年数字工作记忆能力的发展比较

康廷虎，张 丰，范小燕

（西北师范大学 心理学院，甘肃 兰州 730070）

一、引言

工作记忆（working memory）是一种对信息进行暂时性加工和贮存的能量有限的记忆系统，对语言理解、学习、推理、思维等复杂认知任务的完成起关键性作用。［1］Baddeley和 Hitch（1974）在分析记忆信息三级加工模型基础上，提出工作记忆的三系统模型，该模型认为工作记忆由视觉空间模板、语音回路和中央执行系统三部分构成。［2］

在信息的储存、加工过程中，不同的系统起着不同的作用。Baddeley的研究认为多位数运算中的进位给工作记忆增加了负荷，这表明任务的复杂性对于工作记忆的加工过程具有很好的预测性。［3］在此研究基础上，形成了工作记忆的双任务研究范式（dual task paradigms）。它要求被试同时完成两项任务，其中一项是认知任务，简称为主任务，另一项是用于增加工作记忆成分负荷的任务，称为次级任务。双任务范式的基本假设是：如果两项任务同时应用工作记忆的某一成分或资源，那么次级任务将延长主任务的反应时间，或增加错误率。反之，次级任务不会干扰主任务。通过对反应时间或者反应错误率的分析，可以了解工作记忆不同系统的加工特点，同时也可以探讨个体之间的差异。有研究者在数字工作记忆的研究中发现，干扰任务对数字记忆的广度和回忆的正确率存在着重要的影响，从而认为复述是工作记忆信息得以保持的主要原因。［4］连四清、张洪山（2007）研究结果表明，在简单整式和判断任务中工作记忆不同系统的加工对被试的反应存在显著的影响。［5］

由于工作记忆能力可以敏感地反映年龄变化和个体差异，因此有研究者认为工作记忆能力可以作为年龄和个体差异的一项重要指标。［7］目前国内心理学关于工作记忆的研究多以大学生为被试，涉及儿童的工作记忆研究相对较少，尚未有系统的专题研究。［7］在李欢欢、程灶火等人的研究中，以18～49岁之间的成人为被试，对数字工作记忆与年龄之间的关系进行了探讨，结果发现数字工作记忆广度成绩随着年龄的增长而呈现出下降的趋势。［8］

本研究采用双任务研究范式，对不同年级阶段青少年数字工作记忆能力进行测量，旨在了解青少年工作记忆能力的发展变化趋势，分析不同年级阶段青少年工作记忆能力发展的特点。

二、研究方法

（一）调查对象

在本次调查中，选取了不同性别（男151人，52．1%；女139人，47．9%）、不同年级（小学141人、48．6%；初中72人，24．8%；高中77人，26．6%）的290名青少年参加了此次调查。年龄在11—16岁之间，平均年龄为12．56±0．34岁。

（二）测量程序

在研究中应用数字排序测验（the digit ordering test，DOT）的双任务作业范式。［9］要求被试在测试的过程中，对界面上呈现的数学算术题的正误做出判断，并记住算术题的得数，在其呈现完毕之后，要求被试按照算术题呈现的顺序对他记忆的算术题得数进行序列回忆。操作主要包括四个步骤，具体如下：

第一步：呈现指导语1。“屏幕上将会出现一个数学算式，请您判断是否正确并用鼠标点击相应的按钮；同时请记住算式末尾的一个数字。如‘8－4＝5’，要求您记住‘5’这个数字，同时判断这个算式是否正确，如果你认为是正确的，则按‘Y’键，如果认为是错误的，则按‘N’键。当一组题做完后，请按相应数字键将该组算式中每个算式末尾的数字按算式呈现的顺序回忆出来。请按空格键练习三次！”

第二步：练习。按空格键后在屏幕的中央出现一个算式，受测者努力记住算式末尾那个数字，并判断式子是否正确。当受测者按键之后立即显示第二个式子。从每道算术题出现到被试按相应键回答的最长时间间隔为4000ms，超过此时间则呈现下一道。一组算术题呈现完毕之后，呈现指导语2：“请您按相应的数字键，根据算式呈现的顺序，依次输入每个算式末尾的数字！”并显示输入窗口。

如果三次练习中有一次通过，呈现指导语3。如果三次都没有通过，则显示警告“您还有三次练习机会，请按空格键继续练习”。如果仍然不能通过，显示提示语：“练习没有通过！请您找管理员寻求帮助！”

第三步：正式测试。在正式测试中，一组算式中算式的个数从2个开始，依次增加。一组算术题呈现完毕后呈现指导语4：“请您按相应的数字键，根据算式呈现的顺序，依次输入每个算式末尾的数字！”，并显示一个输入窗口。此时预留4000ms的被试反应时间。此外被试按完上一个数字键到按下一个数字键之间也有4000ms的预留时间，超过4000ms仍不反应则终止此轮测试（但若被试在4000ms内给出反应，则按键完毕后开始下一轮）。

如果被试在测试中顺利通过，则呈现指导语5：“恭喜！本级别通过。请点击空格键进入下一级别测试。”进入下一级别测试，如果被试在某个水平上第一次没有通过，则再给他三次机会，如果他有一次通过，则呈现指导语，进入下一级别测试，如果三次仍未通过，则显示指导语6：“本轮测试没有通过！谢谢您使用本测试系统！”

第四步：结果记录。在测试过程中，主要是测试被试最多能回忆的个数。计分以被试正确回忆的个数为标准，正确回忆的个数即被试的得分。

三、测验分数分析

（一）不同年级阶段青少年的数字工作记忆

1．小学生数字工作记忆特点

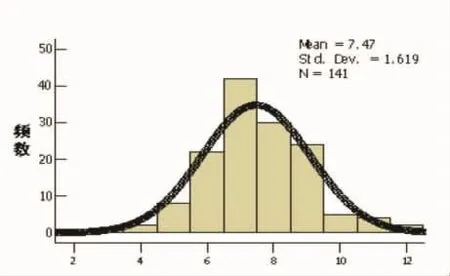
图1 小学生正确回忆项目数的频数分布图

图1是小学生数字工作记忆测验数据频数分布图，从图中可以发现，小学生正确回忆的项目数范围在2～12之间。其中大多数被试的得分在7～8之间。数据分布偏度、峰度检验结果显示，Skewness＝0．007、Kurtosis＝1．043，说明青少年得分的数据分布形态基本接近正态分布，但比正态分布更陡峭。

表1 小学生正确回忆项目数的频数百分位数分析

表1是以10特定百分点的百分位数分析结果，可以发现以10%条件平分的条件下，小学生正确回忆的项目数在10%与20%，30%、40%与50%，60%与70%，80%与90%之间差距并不明显。把小学生正确回忆项目数分为四个等级，即6．00以下为较低水平，6．00～7．00中等水平，7．00～9．00良好水平，9．00以上为优秀水平，可以发现不同等级的青少年得分存在着显著性差异（F（3，137）＝290．313，p＜0．05），事后检验也发现，不同等级之间的差异均达到显著性水平。

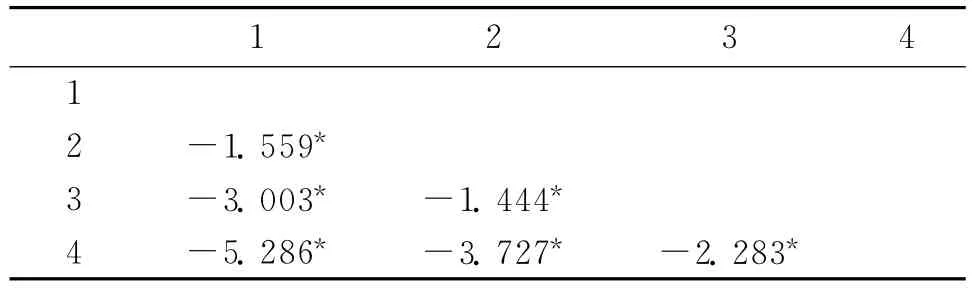
表2 四分位等级条件下小学生得分的事后比较

2．初中青少年数字工作记忆特点

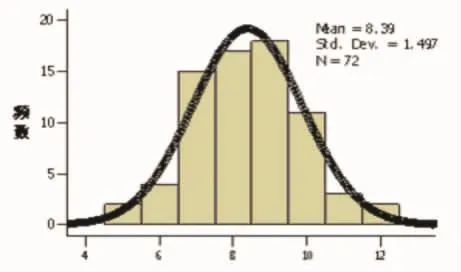
图2 初中生正确回忆项目数的频数分布图

图2是初中生数字工作记忆测验数据频数分布图，从图中可以发现，初中生正确回忆的项目数范围在5～12之间。其中大多数受测者的得分在7～10之间。数据分布偏度、峰度检验结果显示，Skewness＝0．104、Kurtosis＝－0．060，说明青少年得分的数据分布形态为正偏态分布，而且比正态分布更平坦。

表3 初中生正确回忆项目数的频数百分位数分析

表4 四分位等级条件下初中生得分的事后比较

表3是以10特定百分点的百分位数分析结果，可以发现以10%条件平分的条件下，初中生正确回忆的项目数在10%与20%，30%、40%与50%，60%与70%，80%与90%之间差距并不明显。把初中生正确回忆项目数分为四个等级，即7．00以下较低水平，7．00～8．00中等水平，8．00～9．00良好水平，9以上为优秀水平，可以发现不同等级的生得分存在着显著性差异（F（3，137）＝190．865，p＜0．05），事后检验也发现，不同等级之间的差异均达到显著性水平。

3．高中生数字工作记忆特点

图3 高中生正确回忆项目数的频数分布图

图3是高中生数字工作记忆测验数据频数分布图，从图中可以发现，高中生正确回忆的项目数范围在3～13之间。其中大多数受测者的得分在7～10之间。数据分布偏度、峰度检验结果显示，Skewness＝－0．532、Kurtosis＝0．630，说明青少年得分的数据分布形态为负偏态分布，而且比正态分布更陡峭。

表5 高中生正确回忆项目数的频数百分位数分析

表5是以10特定百分点的百分位数分析结果，可以发现以10%条件平分的条件下，高中生正确回忆的项目数在30%与40%，50%、60%与70%之间差距并不明显。把高中生正确回忆项目数分为四个等级，即7．00以下为较低的水平，7．00～9．00为中等水平，9．00～10．00 为较好水平，10．00以上为优秀水平，可以发现不同等级的青少年得分存在着显著性差异（F（3，73）＝111．871，p＜0．05），事后检验也发现，不同等级之间的差异均达到显著性水平。

表6 四分位等级条件下高中生得分的事后比较

（二）青少年数字工作记忆能力的比较

1．不同年级阶段青少年数字工作记忆能力的比较

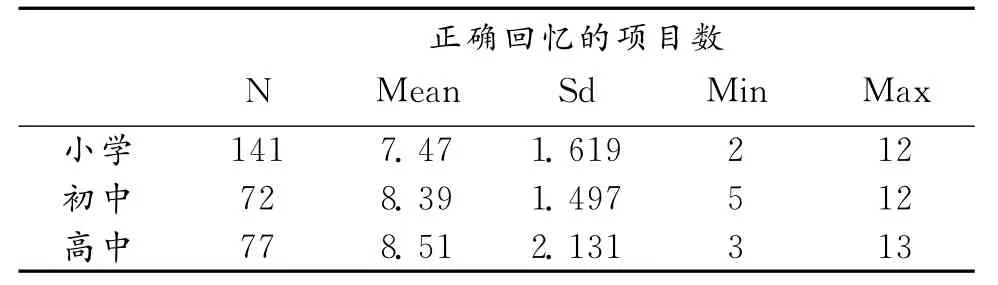
表7 不同年级青少年能够正确回忆数字项目数的描述统计

描述统计分析结果显示，随着年级的升高，青少年能够正确回忆的数字项目数逐渐增加，小学生平均能够正确回忆的项目数为7．47，初中生能正确回忆的项目数为8．39，高中生能够正确回忆的项目数为8．51。方差分析结果显示，不同年级青少年的数字工作记忆能力存在着显著性差异（F（2，287）＝11．578，p＜0．05）。其中小学生的成绩显著低于初中生、高中生的得分，初中与高中青少年的成绩并不存在显著性差异。

2．不同性别青少年数字工作记忆能力的比较

表8 不同性别青少年能够正确回忆数字项目数的描述统计

描述统计分析结果显示，女生能够正确回忆的数字项目数比男生能够正确回忆的项目数多，也就说女生的得分高于男生的得分（M男＝7．89，M女＝8．06，M男＜M女），方差分析结果显示，不同性别青少年的数字工作记忆能力并不存在显著性差异（F（1，288）＝0．698，p＞0．05）。

四、讨论

数字记忆既是人类日常生活中必须要具备的能力，又是学习抽象数学知识的基础。由于青少年数字工作记忆能力受到思维发展和成熟的影响，对年龄的变化有很强的敏感性，因此要了解青少年工作记忆能力的特点，首先就需要对青少年数字工作记忆能力的发展特点予以考察和分析。对小学、初中、高中三个年级阶段青少年工作记忆能力的分析可以发现，青少年工作记忆测验得分的分布近似正态分布，尽管各年级阶段青少年在四分位距各等级的得分不同，但是不同等级之间的差异均达到显著性水平。这表明在不同的年级阶段，青少年工作记忆能力的发展是有差别的。根据Baddeley（1986）的观点，工作记忆任务需要同时进行加工和存储。［10］在本研究中，采用双任务研究范式，在要求被试对算术运算进行正误判断的同时，记住运算的得数。对算术运算正误的判断实际上就是抗干扰的加工过程，而对运算得数的记忆则是存储过程，这两个过程是同时进行的。受个体差异的影响，不同年级阶段的青少年对干扰任务的加工能力是不同的，进而会影响对数字的存储。因此即使是同一年级阶段，青少年数字工作记忆的能力也是不同的，这可能是各年级阶段青少年数字工作记忆得分分布近似正态分布，而且各等级之间存在显著性差异的原因。

对不同年级阶段之间的比较发现，随着年级的升高，青少年数字工作记忆的容量呈现出上升的趋势，不同年级阶段青少年数字工作记忆能力存在着显著性差异，其中小学阶段和初中、高中阶段的青少年数字工作记忆容量的差别较大，但是初中和高中阶段青少年的数字工作记忆容量的差别较小。就发展变化趋势而言，这一结果与李欢欢、程灶火的研究是不同的。这可能是因为本研究选择的被试是从小学到高中阶段的青少年，而在李欢欢等人的研究中，所选择的被试是18～49岁之间的成人。［8］综合两项研究结果可以发现，随着年龄的增长，人们的数字工作记忆能力也是发展变化的，而且在不同年龄阶段，其变化发展的趋势也是不同的。

在对不同年级阶段青少年工作记忆能力的发展变化趋势的分析中发现，从小学到高中阶段，青少年工作记忆能力是持续升高的，而且在不同年级阶段，这种发展变化的速度是不同的，从小学到初中，青少年数字工作记忆能力的发展较快，而在初中阶段到高中阶段，青少年数字工作记忆能力的发展则明显减缓。这一方面可能与运算任务有关，本研究采用了数字界于1～9之间的简单加减算术运算任务。与多位数运算或者乘除运算任务不同，不同年级阶段的青少年对简单运算任务都是比较熟悉的，因此在数字工作记忆测量的过程中，如果不同年级阶段青少年对于干扰任务的加工不同，那么这种简单运算任务对于数字的储存更敏感。另一方面，因为工作记忆是一个需要在很短的时间内进行注意资源配置、加工任务转换的过程，［11］不同年级阶段青少年的认知加工、任务转换能力可能是不同的。有研究表明，工作记忆的广度对儿童算术认知的策略应用具有重要的影响，［12］而在张林（2006）等人的研究中发现，青少年的工作记忆ERP存在着年龄效应，年龄因素影响着大脑的加工过程。随着年龄的增长，青少年的反应逐渐加快，正确率也明显提高。［13］这为本研究结果提供了支持。

性别差异的比较是差异心理学研究的主要内容之一。对18～49岁之间不同性别成人工作记忆能力的比较发现，男女性在数字工作记忆能力方面并不存在差异，但是男性成绩略高于女性的成绩。［8］在本研究中，对不同性别青少年的数字工作记忆能力进行了比较，结果发现，与男性青少年相比，女性青少年在数字工作记忆的测量中得分较高，但是不同性别之间并不存在显著性差异。Rosenberg和Park（2002）等人的研究认为，男女性工作记忆广度的不同亚结构的变化趋势是基本一致的，［14］在本研究中数字工作记忆能力的计分是以被试能正确回忆的简单算术运算式得数的个数为标准，正确回忆的个数即被试的得分，实际上同样是考察了不同性别被试数字工作记忆的广度，因此不同性别青少年数字工作能力没有表现出显著性差异。

［1］Baddeley A．The fractionation of working memory．Procession．National ．Academy of．Sciences．1996，93（11）：13468－13472．

［2］Baddeley A D，Hitch G．Working memory．In：G．A．Bower．The psychology of learning and motivation．New York：Academic Press，1974，8．

［3］王恩国．工作既已与学习能力的关系［J］．中国特殊教育，2007，（3）：78－84．

［4］Logie R H．，Gihooly K J，Wynn V．Counting on working memory in problem solving．Memory＆Cognition，1994，22：395－410．

［5］连四清，张洪山，林崇德．工作记忆在简单整式和判断中的作用［J］．心理发展与教育，2007，（3）．

［6］Jenkins L，Myerson J，Halle S，Fry A F．Individual and developmental differences in working memory across the life span，Psychonomic Bulletin and Review，1999，6：28－40．

［7］顾敏敏，鲁忠义．儿童的工作记忆广度［J］．心理科学，2004，27（1）：137－139．

［8］李欢欢，程灶火，王力，等．成人数字、词语和视空间工作记忆广度的发展特征及影响因素［J］．中国心理卫生杂志，2006，20（4）：248－251．

［9］张拉艳，周世杰．工作记忆及其评估［J］．中国临床心理学杂志，2005，13（3）：360－362．

［10］Baddeley A D．Working memory．Oxford，England：Clarendon Press．1986．

［11］刘惠军，郭德俊．工作记忆的性质工作机制［J］．首都师范大学学报（社会科学版），2006，（1）．

［12］陈英和，王明怡．工作记忆广度对儿童算术认知策略的影响［J］．心理发展与教育，2006，（2）．

［13］张林，刘昌．青少年工作记忆的年龄差异：脑事件相关电位研究［J］．中国临床心理学杂志，2006，14（5）：542－546．

［14］Rosenberg L，Park S．Verbal and spatial functions across the menstrual cycle in healthy young women．Psychoneuroendocrinology，2002，277：835－84．