双液滴同时垂直撞击液膜数值研究

刘 红， 贾 小 娟， 解 茂 昭， 冯 倩

（大连理工大学 能源与动力学院，辽宁 大连 116024）

0 引 言

液滴撞击液膜或壁面是一种常见的工程现象，例如：内燃机的燃料喷射［1］、喷雾冷却［2］、喷墨打印、冷喷涂［3］等.这些现象是大量液滴连续碰撞壁面造成的，首先是液滴碰撞干壁面形成液膜，后续液滴则碰撞在已经形成的液膜上，随着碰壁液滴的增加，液膜积聚，厚度变化，液滴碰撞的演化规律随着液膜厚度的变化有明显的变化.对该现象的研究主要有两种方法：一种是基于拉氏的粒子跟踪方法，另一种是基于界面跟踪的方法.基于粒子跟踪的方法不考虑液滴的形状变化，用统计方法将大量液滴划分为具有代表性的几个油滴包元，可以得到喷雾碰壁的统计规律，但无法得到液滴碰壁过程中形状变化等的细节特性.由于液滴碰壁过程中存在液滴与壁面或液膜相互作用，形状变化对液滴后续演化过程影响甚大，了解演化细节有利于掌握相互作用的物理机制，故有大量文献从单液滴出发，研究单液滴与壁面或液膜碰撞过程的演化规律.由于工程实际中最常见的是连续液滴与液膜或壁面碰撞，有必要掌握多液滴耦合作用的物理机制，故对多液滴碰壁的研究具有重要的实践意义.Roisman等［4］实验观测和理论分析了两个液滴撞击固体表面的流动现象.Fujimoto等［5］对两个液滴接连撞击固体壁面进行实验观测和数值模拟，定性地分析了液滴撞击速度对流动状态的影响.Guo等［6］用VOF法对两个液滴同时撞击薄膜的过程进行了数值研究，观察了双液滴同时撞击液膜后的流动情况.从文献可见，多液滴与液膜或壁面碰撞过程受到液滴自身运动和液滴间相互作用的影响，流动及演化过程非常复杂，但目前研究多是定性分析，定量研究还需进一步深入.

对双液滴碰撞液膜动力学特性的研究，很大程度上可以反映多液滴碰壁的情况.本文对双液滴同时垂直撞击同种液膜进行数值研究，目的是揭示碰撞后的动力学特性，探讨We和液滴间距s对流动结果的影响，为多液滴碰撞液膜的研究提供定量的依据.

1 数理模型及求解方法

1.1 数理模型

研究对象的初始状态如图1所示，两液滴同时以相同速度垂直撞击液膜，液滴与液膜为同种流体.两液滴中心间距为s，液膜厚为h.为简化问题，假设液滴撞击液膜前为球形，液滴和液膜组成的液相为不可压牛顿流体，流体黏性系数及表面张力系数为常数，整个撞击过程为非稳态，并且流动为层流，气液界面无相变，无传热传质.考虑重力作用的影响，整个流动过程的控制方程为连续方程和动量方程.

连续方程：

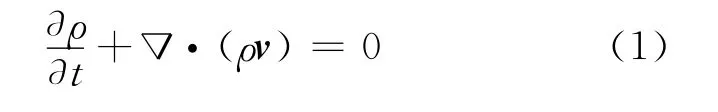
动量方程

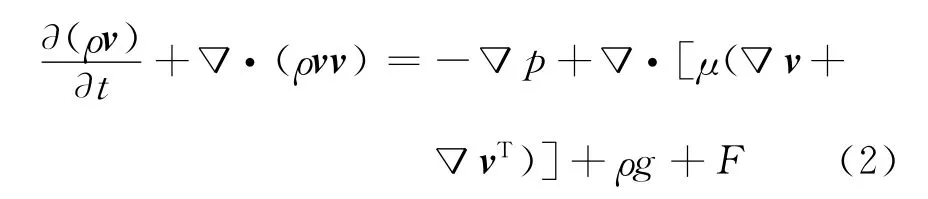
式中：v表示速度矢量；t表示计算时间；p表示压力；g表示重力加速度；F表示单位体积的表面力.

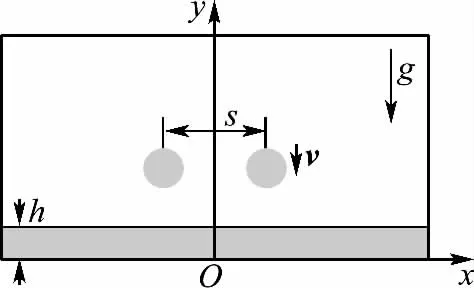
图1 物理模型初始时刻示意图Fig.1 The physical model at initial time

1.2 界面跟踪方法

气液两相界面的捕捉采用VOF法.VOF法通过计算单元格内流体体积比函数C来确定自由面.定义C为控制体内气体所占的体积与控制体的总体积之比.

则体积分数的具体形式如下：

体积分数的输运方程如下：

通过控制单元内及与之相连控制单元内的C值，运用重构技术得到液滴界面，从而确定其形状及尺寸.

1.3 网格局部自适应

自由界面附近网格的质量对精确捕捉自由面非常重要，而远离界面的流动变化对界面跟踪影响不大.局部自适应则是指计算过程中，根据体积分数的梯度值细化界面附近网格和粗化远离界面的网格.一次加密可以实现一个四边形网格划分成4个小网格，网格粗化则相反.自适应时网格粗化至原始网格后即不能继续粗化.采用局部细化网格的方法不仅能够准确跟踪自由界面，而且大大降低了计算成本.

本文应用三次网格局部自适应方法，二维模型初始网格数为5 040，应用三次网格局部自适应所需网格数不超过50 000.如果完全应用结构化网格，则需要322 560个网格.应用此方法后，可以节约10倍左右的计算时间.

1.4 边界条件及数值细节

用流体计算软件FLUENT6.3对双液滴同时垂直撞击等温液膜壁面进行了数值模拟研究.壁面张力采用CSF模型，自由表面的追踪采用VOF法.二维模拟中，计算区域为对称二维长方形，采用无滑移的壁面边界条件、对称边界条件及压力出口边界条件.三维计算区域为长方体，采用同样的边界条件.如图1所示，y轴处为对称边界，底边及侧边为壁面，上方为压力出口.重力方向为y轴负方向.用有限容积法对偏微分方程进行了离散，动量方程的离散基于二阶迎风格式，压力速度耦合使用 PISO 格式，用 Body Force Weighted进行压力离散.时间离散应用一阶差分格式.所有变量残差小于10－6时认为计算已收敛.

2 结果与讨论

与双液滴撞击液膜问题相关的物理量主要为液滴的直径d0、液滴初始速度u、液滴之间的距离s、液膜厚度h和气液两相的物性参数.液滴与液膜均为正庚烷，气相介质为空气.正庚烷的物性参数如下：密度ρ＝684kg／m3，黏度系数μ＝4.09×10－4Pa·s，表面张力系数σ＝0.02N／m.本文中，分别考虑We和液滴间距s对双液滴撞击液膜流动行为的影响.计算参数见表1.从Case1至Case7保证量纲一液膜间距s／d0一致.该模型已经过验证［7］.

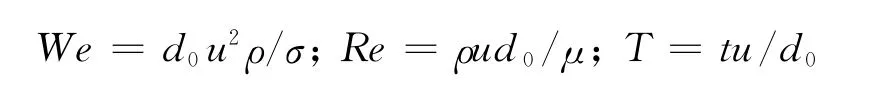
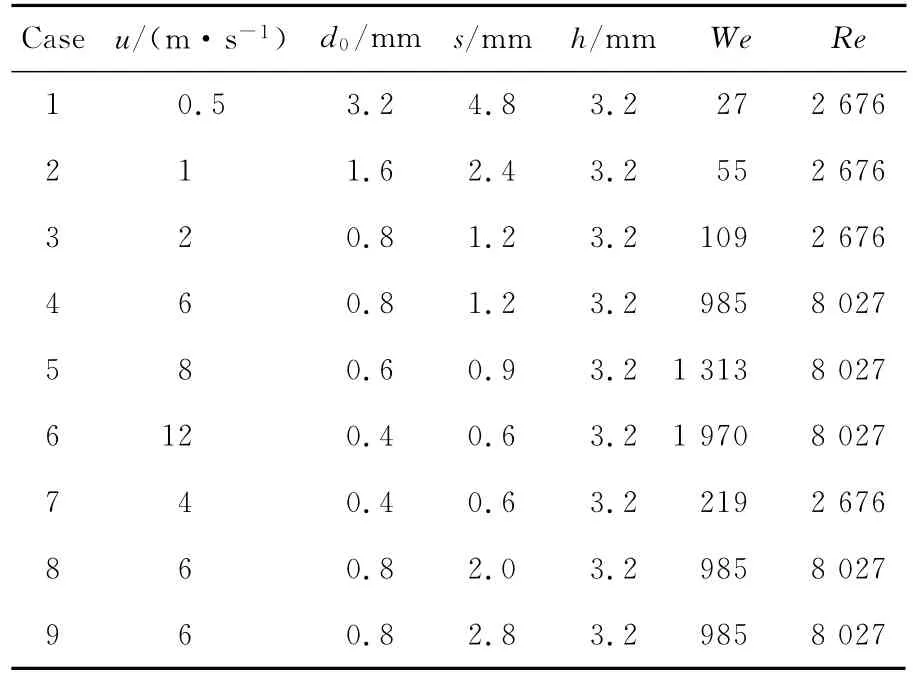
表1 计算参数Tab.1 Parameters for calculation

2.1 碰撞动力学行为

两平行液滴垂直碰撞液膜问题具有明显的三维特性，本文对Case2进行了三维数值模拟.三维计算中，由于电脑硬件及计算时间所限，只对含有液滴碰壁引起表面变形的部分区域气液两相界面进行了网格自适应，其他区域虽包括液膜与空气间的两相界面，但不进行网格自适应，仍为粗网格.三维模型初始网格为24 000个，自适应后达到最大网格数550 000.图2为对Case2进行三维模拟得到的空间液膜演化图.可以看出，液滴撞击液膜初期流动现象与单液滴撞击液膜相似［8］.撞击初期，两液滴与液膜接触，进行动量交换，并发生黏性变形，在动量力、黏性力及表面张力共同作用下，形成表面波动；随着时间的发展，两个液滴下落点形成两个深坑，两个表面波动相遇并发生撞击，形成中心薄壁液膜射流，水花与射流达到最大高度后在重力作用下开始回落.Case2由于We较小（We＝55），液滴初始动力不足以克服黏性力和表面张力，没有产生二次液滴，中心射流回落期间发生断裂.三维计算应用服务器并行进行，用时30d.

为节约计算时间，采用二维平面模型，对该问题进行计算，二维模型基础网格数为5 040，自适应后达到网格数50 000左右.二维模型可以比三维模型空间步长更小.图3是取三维模拟中两液滴中心垂直剖面与二维模拟结果的比较.从图中可以看出，二维模拟结果与三维模拟结果比较吻合，但是对同一时刻，二维空间液膜的高度高于三维模拟结果，这是由于二维模型中无法展现中心液膜的三维特性，同时也由于三维模型网格空间步长不够细，空间步长更小的二维模型可以捕捉到尺寸更小的液滴和薄液膜.模拟结果表明，二维模型可以在一定程度上反映双液滴撞击液膜的动力学特性，而且可以更加准确地追踪空间液膜的细小变化.以下模拟皆采用二维模型进行计算.

2.2 We影响

根据Cossali等［8］的研究，液滴撞击液膜时存在一个临界We用以判断是否有飞溅发生.在大量数值试验基础上，本文取We分别为27、109及219进行验证.空间液膜随时间的发展如图3（b）及图4所示，可以看出，即使We很小（We＝27），也会出现中心射流破碎，且随着We的增大，射流破碎更加剧烈，破碎后形成的二次液滴尺寸更小；前三者水花处都没有飞溅，但Crown空间液膜厚度随着We的增大而变薄，当We为219时，空间液膜已足够薄，已发生破碎，形成飞溅.对比4种情况可以看出，随着We的增大，空间液膜的厚度变薄.We决定了是否有飞溅发生，对空间液膜的发展也有重要的影响.

图2 Case2空间液膜时空进化Fig.2 The evolution of space liquid membrane of Case2

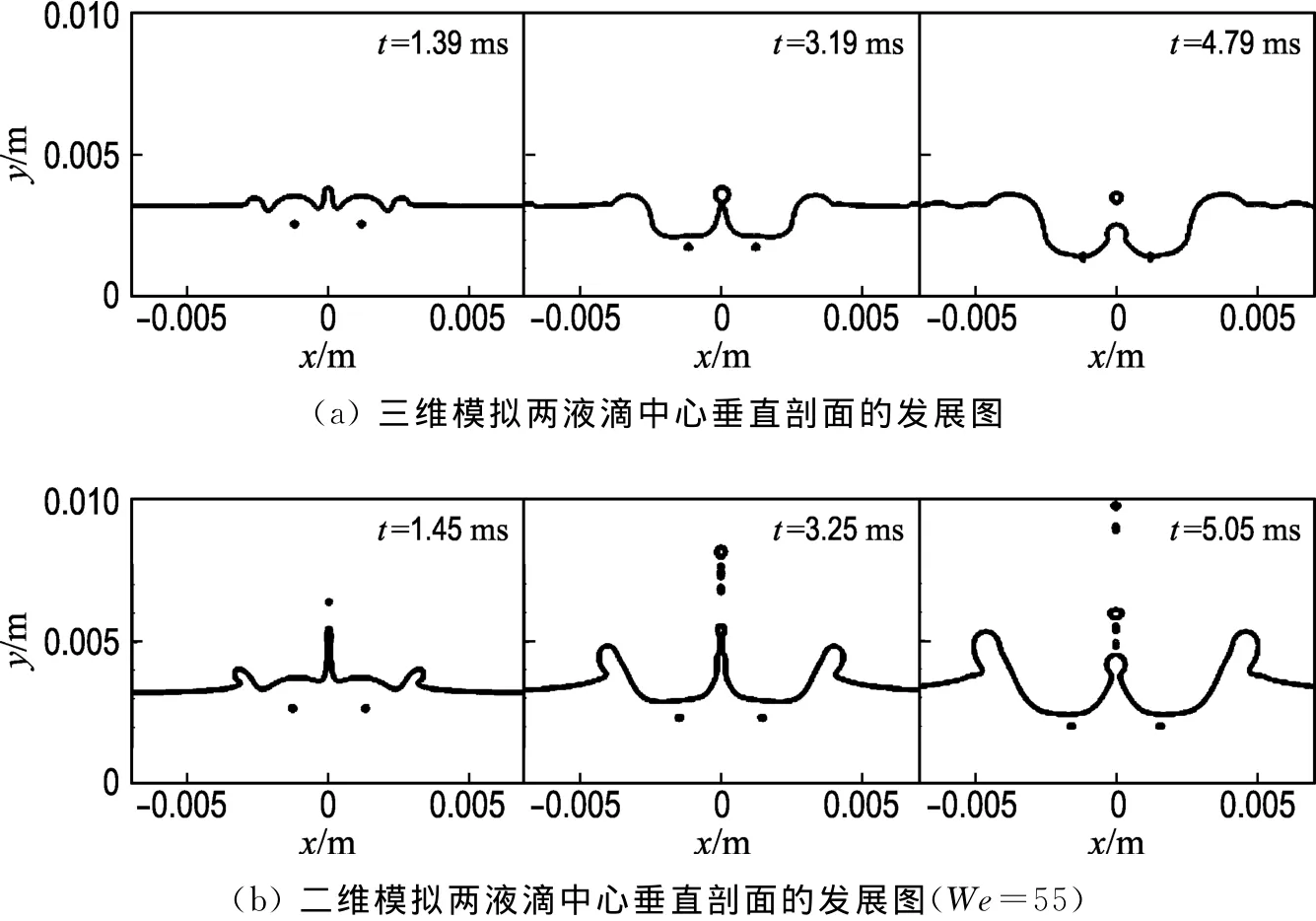
图3 二维模拟与三维模拟两液滴中心垂直剖面流动发展对比Fig.3 The contrasts of 2Dtwo droplets flow at centre normal section with that of 3D

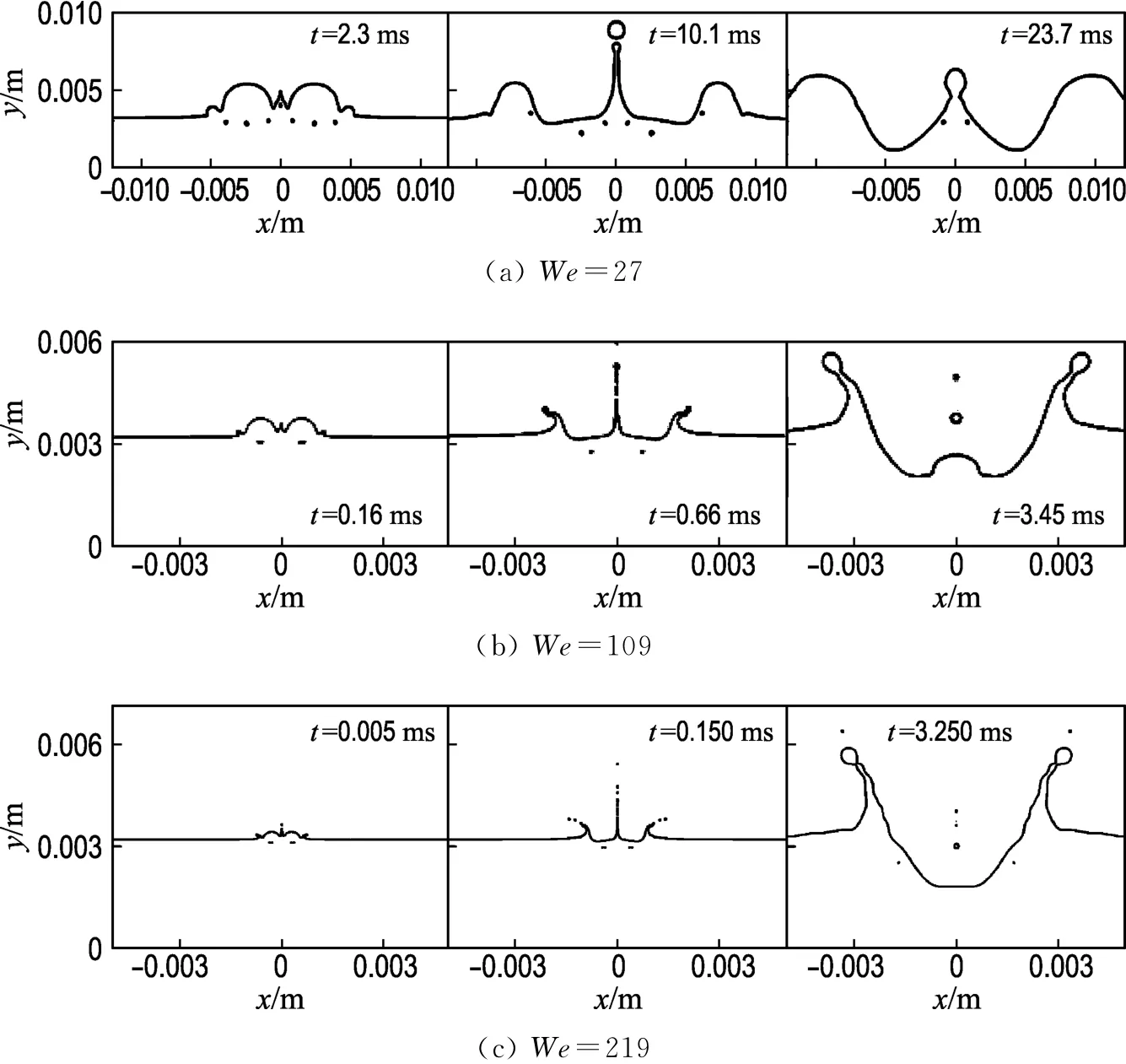
图4 不同We下空间液膜随时间的发展Fig.4 The evolution of space liquid membrane at different We

为了分析水花和飞溅液滴随We变化的发展情况，特对图5所示的水花高度Hd、射流高度Hs和水花边缘到y轴的距离L及二次液滴的数量和尺寸进行定量研究.

图6为We分别为985、1 313与1 970时水花尺寸随时间的发展趋势.从图中可以看出，水花高度Hd随时间先增加，到最大高度后经历几次脉动，而后逐渐降低；量纲一中心射流高度Hs先瞬时升高，在短时间内即开始脉动，达到最大高度后开始降低，这是由于射流迅速破碎，Hd和Hs都会随着We的减小而增大，开始回落的时间也随着We的减小而延后.

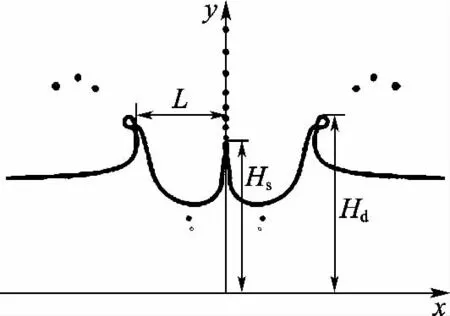
图5 飞溅参数定义Fig.5 Definition of impingement characteristics

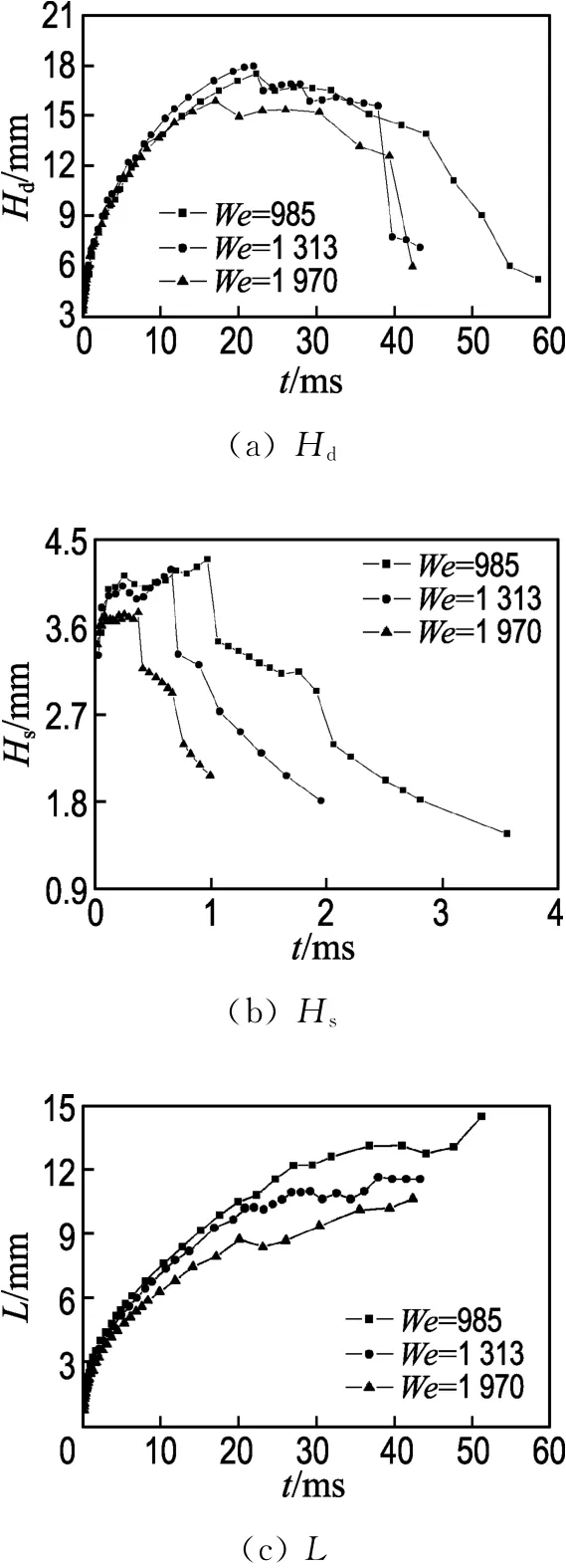
图6 We对空间液膜的影响Fig.6 The effects of We on the space liquid membrane

液滴碰撞液膜后形成的二次液滴的数量和尺寸是反映飞溅程度的重要参数，二次液滴几何平均直径d10是指某时刻空间内所有二次液滴直径的平均值.如图7（a）和图7（b）所示，65%的二次液滴直径在0.06～0.20mm，小部分直径小于0.06mm的液滴无法被捕捉到，可以看出二次液滴的直径分布呈现近似二次分布的规律.二次液滴的几何平均直径d10随时间发展初期增长速度较快是由于中心射流破碎较早，产生大量小液滴，随着时间的推移，中心射流区液膜逐渐增厚，破碎的二次液滴直径增大；后期二次液滴主要来源于水花破碎飞溅，形成的二次液滴比中心射流破碎的直径更大，且随着时间的推移增长趋于平缓，图中曲线结尾处说明到此时已无二次液滴再继续生成.比较3种We下的二次液滴尺寸分布（图7（a））及二次液滴几何平均直径随时间发展（图7（b））可知，随着We的增大，更多而且尺寸更小的二次液滴生成.这些变化可以用动能的增大来解释，We增大代表液滴动能影响增大，克服表面张力束缚能力愈强，空间液膜的发展更充分，形成的液滴数量更多，尺寸更小.

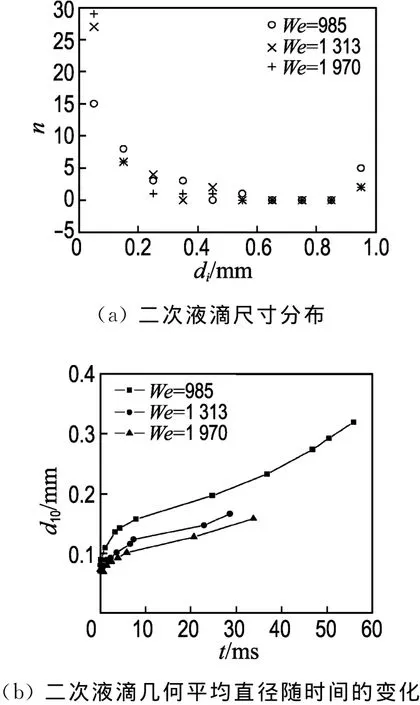
图7 We对二次液滴的影响Fig.7 The effects of We on the secondary droplets

2.3 两液滴中心间距的影响

用Case4、Case8和Case9考察液滴中心间距变化的影响.如图8（a）所示，液滴间距的变化对水花发展时期几乎没有影响，而水花回落速度稍有不同，但差别不大.从图8（b）看出，随着液滴间距的减小，最大射流高度显著变小，中心射流开始回缩的时间越早，回落到液膜处产生射流波的时间也越早，导致了水花回缩速度的不同.液滴间距越小，中心区两空间液膜碰撞开始得越早也越激烈，此时液膜的径向速度还很大，两碰撞的液膜形成相互剪切力，更易形成中心射流破碎.从图8可以看出液滴中心间距对射流发展有明显影响.如图9所示，随着液滴间距的减小，二次液滴的生成也越早.所生成的二次液滴直径在0.1～0.2mm居多，整体呈现近似正态分布规律.二次液滴几何平均直径随时间变化的差别主要在于射流处生成二次液滴情况的不同.

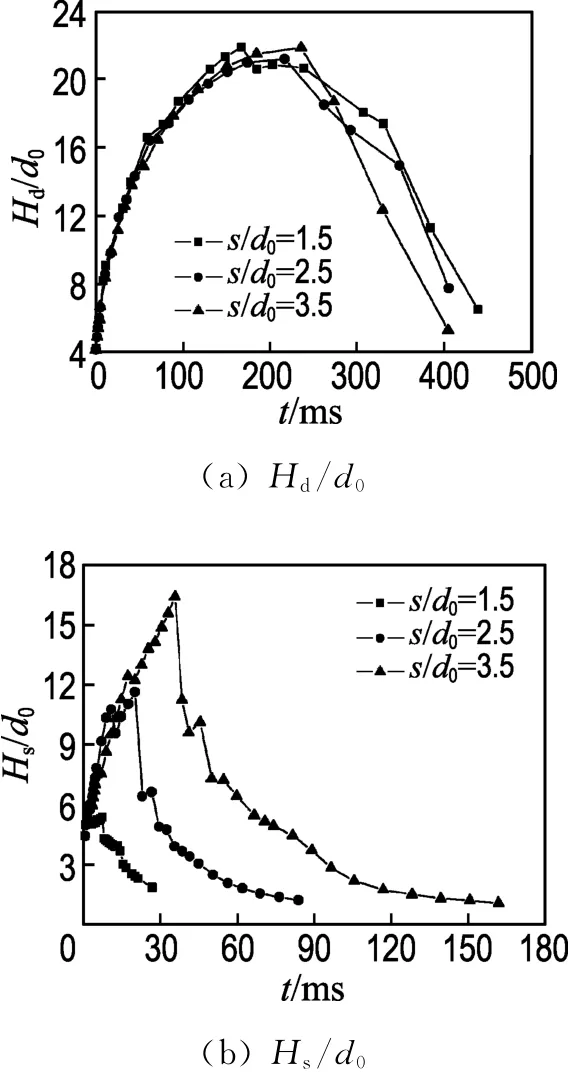
图8 液滴间距对空间液膜的影响Fig.8 The effects of distance between the two droplets on the space liquid membrane

图9 液滴间距对二次液滴的影响Fig.9 The effects of distance between the two droplets on the secondary droplets

3 结 论

（1）双液滴撞击液膜除了形成表面波动及皇冠形空间液膜外，两表面波相撞还会形成中心薄壁液膜射流.中心射流产生的二次液滴尺寸比皇冠形空间液膜生成的液滴尺寸小.中心射流回落期间也会发生断裂，形成二次液滴，即使We很小，也会出现中心射流破碎，且随着We的增大，射流破碎更加剧烈，破碎后形成的二次液滴尺寸更小.

（2）We决定了水花顶端是否有飞溅发生，We较小时不能产生二次液滴飞溅，随着We的增大，空间液膜的厚度变薄，且生成更多而且尺寸更小的二次液滴.

（3）液滴间距的变化对水花发展时期几乎没有影响，而对中心射流高度影响显著，液滴间距越小，越易形成中心射流破碎，形成的二次液滴越小.

［1］Motzkus C，Gensdarmes F，Gehin E.Parameter study of microdroplet formation by impact of millimetre－size droplets onto a liquid film ［J］.Journal of Aerosol Science，2009，40（8）：680－692.

［2］史中远，陈文奎，张春明，等.小温差喷雾碰壁蒸发过渡段换热特性分析［J］.工程热物理学报，2008，29（3）：469－472.SHI Zhong－yuan，CHEN Wen－kui，ZHANG Chunming，etal.Analysis of heat transfer characteristics of spray impinging evaporation in transition region under small temperature differences ［J］.Journal of Engineering Thermophysics，2008，29（3）：469－472.（in Chinese）

［3］EI－Hadj A A，Zirari M，Bacha N.Numerical analysis of the effect of the gas temperature on splat formation during thermal spray process ［J］.Applied Surface Science，2010，257（5）：1643－1648.

［4］Roisman I V，Prunet－Foch B，Tropea C.Multiple drop impact onto a dry solid substrate［J］.Journal of Colloid and Interface Science，2002，256（2）：396－410.

［5］Fujimoto H，Ogino T，Takuda H.Collision of a droplet with a hemispherical static droplet on a solid［J］.International Journal of Multiphase Flow，2001，27（7）：1227－1245.

［6］GUO Jia－hong， DAI Shi－qiang.Numerical simulation on the mechanism of the normal impact of two droplets onto a thin film ［J］.Journal of Shanghai University：English Edition，2007，11（3）：210－212.

［7］LIU Hong，XIE Mao－zhao，WANG Su－chun，etal.Numerical study on impingement of a droplet upon a liquid film ［J］.Applied Mechanics and Materials，2011，44：2499－2503.

［8］Cossali G E，Coghe A，Marengo M.The impact of a single drop on a wetted solid surface ［J］.Experiments in Fluids，1997，22（6）：463－472.