不同截面型式抗滑桩加固边坡数值分析

年 廷 凯＊1，2， 徐 海 洋， 李 东 晨

(1.大连理工大学 土木工程学院，辽宁 大连 116024；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；3.深圳冶建院建筑技术有限公司，广东 深圳 518054；4.中国电力工程顾问集团中南电力设计院，湖北 武汉 430071)

0 引 言

抗滑桩是滑坡防治的一种工程建筑物，其设计是典型的土木工程问题，需综合考虑复杂的岩土工程条件和结构工程相关问题.抗滑桩设计标准最初由地矿行业编制并施行[1]，其在很大程度上改变了我国滑坡防治技术的面貌，并在计算理论等方面有所发展[2－3].1975年，Zienkiewicz等[4]提出了抗剪强度折减法(shear strength reduction method)，后被广泛应用于边坡稳定性分析.Griffiths等[5－6]以有限元强度折减法对二维和三维边坡的稳定性进行数值分析，证实了边坡稳定性有限元法的有效性和优越性.随着计算机技术的发展，抗滑桩加固边坡数值分析迅速展开[7－11].与此同时，土拱问题[9－14]的探讨也随之而生.土拱效应是指桩间土体和桩后土体位移不一致，土体抗剪能力发挥导致土体中形成所谓“楔紧”作用.1943年，Terzaghi[15]通过活动门试验证实了土拱的存在，指出了土拱效应的一般性，并给出形成土拱的必要条件.

目前圆形和矩形是两种最常见的抗滑桩截面型式.一般情况下，矩形截面抗滑桩适用于滑坡滑动方向或者推力方向确定的工况下(我国多采纳这一型式)；圆形截面桩适用于滑坡推力方向难以确定或预加固潜在滑移坡体.不同的抗滑桩截面型式影响着边坡的加固效果，也决定了施工方法和工程造价.鉴于此，针对几种典型截面型式的抗滑桩，探讨边坡加固后的安全系数和桩身内力反应以及不同桩型的抗滑桩间土拱分布情况，以期为抗滑桩规范修订和工程设计提供参考.

1 分析模型及数值验证

采用 Cai等[7]、Won等[9]和 Wei等[10]的典型边坡算例(图1).抗滑桩加固于边坡中部，模型的几何参数为边坡的坡度V∶H＝1∶1.5，坡高H＝10.0m，坡体水平长度L2＝15.0m，坡后缘长度L1＝15.0m，前缘长度L3＝10.0m，地基深度为10.0m，上部不稳定土层厚度Hu＝15.0m，下卧稳定土层(岩层)厚度Hs＝5.0m；桩心距坡脚的水平距离Lx＝7.5m，桩形心之间的距离s＝3.0m；桩长统一取Lp＝13.0m(嵌入岩层约3m).抗滑桩－边坡土性参数列于表1.

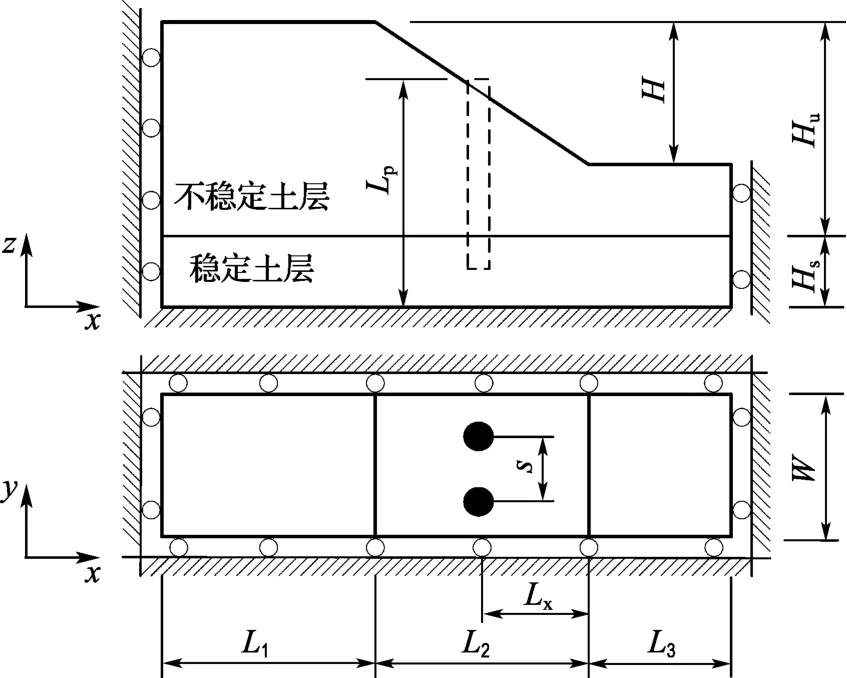
图1 计算模型Fig.1 Computational model

表1 抗滑桩－边坡土性参数Tab.1 Property of slope－pile

利用服从Mohr－Coulomb破坏准则与非关联流动法则的理想弹塑性本构模型和相应计算程序，以数值迭代不收敛联合坡面特征点位移陡增作为边坡失稳判据，计算出加固前边坡(模型宽度y＝3.0～16.0m)的安全系数在1.126～1.198，与 Cai等[7]、Won等[9]和 Wei等[10]所得的安全系数1.13～1.20基本一致 .在此基础上，考虑抗滑桩加固边坡，将桩视为理想线弹性体，取桩和土的弹性模量分别为60GPa和200MPa，圆形截面桩桩径D＝0.8m，桩间距与桩径之比s／D＝3，其他参数不变；考虑桩土间的接触相互作用，摩擦因数取为0.3，计算获得加桩后边坡安全系数为1.734，与 Wei等[10]利用有限差分法所得结果1.72相一致，由此表明上述方法是可行的.

选择6种代表性抗滑桩截面型式(如T形、正方形、矩形、正五边形、正六边形和圆形等)，探讨不同截面型式的抗滑桩加固效果.图2给出了6种不同截面型式下的计算模型以及网格的整体和局部剖分情况.6种模型的边界条件相同，即边坡模型的前后和左右两个侧面约束法向位移，底部边界采用固定约束.为了进行合理的比较，给出参数一致性原则:(1)桩材料相同，且桩的横截面面积S相同，均为1m2；(2)桩心间的距离(形心距)相同，均为3.0m.各截面型式抗滑桩的周长L、惯性矩Iy、截面系数Wx、Wy等参数列于表2.土与桩均采用六面体减缩积分单元(C3D8R)，通过对桩周土体网格的局部加密，削弱接触面单元的病态条件对计算的影响.

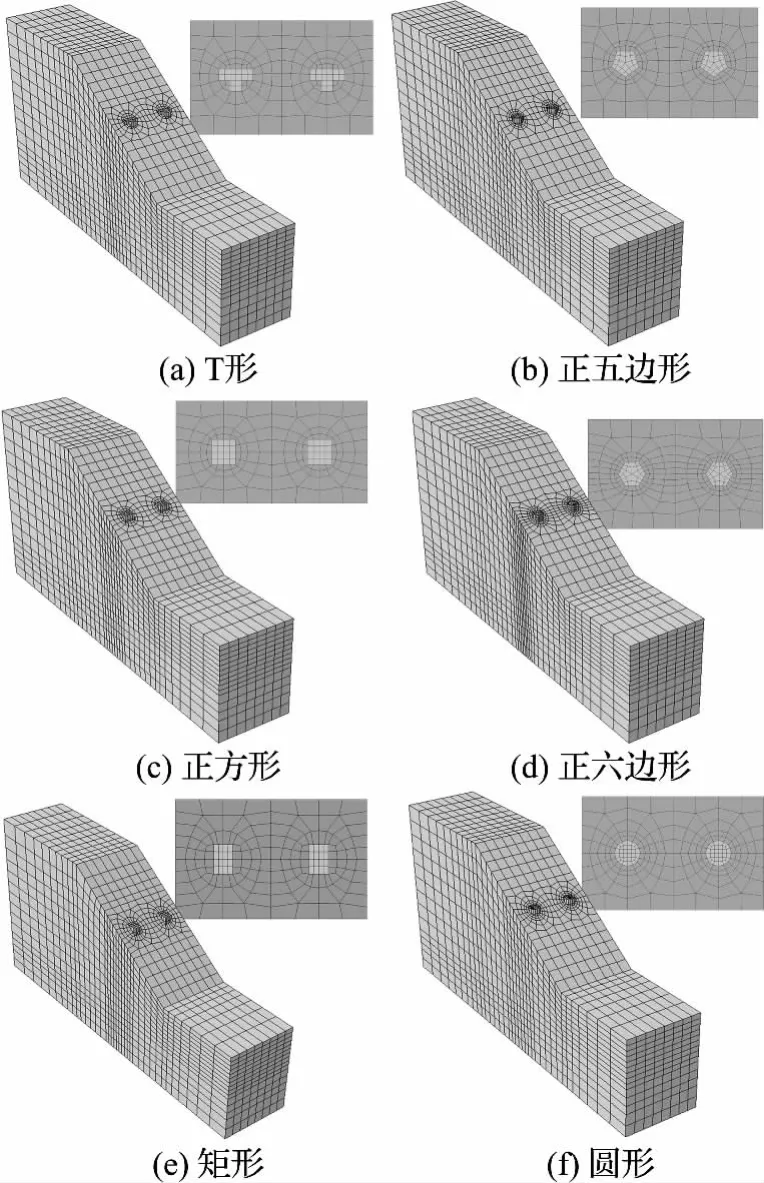
图2 6种截面型式的抗滑桩计算模型及网格型式(相同截面面积和桩心距)Fig.2 Calculation models and mesh types for six pile cross－sections(the same area of cross－section and pile－center distance)

合理选取网格密度是准确、高效计算的前提条件.为此，以圆形截面桩为例建立了3种不同密度的有限元网格，如图3(a)、(b)和(c)所示(模型底面:Z＝0).3种网格都是在桩身附近局部加密，远离坡体逐步稀疏；其中图3(a)是图2中采用的标准网格，其网格平均尺寸为1m，图3(b)网格平均尺寸为0.667m，图3(c)网格平均尺寸为0.5 m.3种有限元网格计算所得的安全系数列于表3.此外，表3还给出了正方形截面桩在3种不同网格密度下的安全系数.分析表3可见，随着网格加密，安全系数变化幅度很小，约为1%，但计算时长却大大增加；另一方面，不管是正方形还是圆形截面桩加固边坡，其安全系数均随着网格变化呈现出相同的变化规律.由此可见，采用图2的网格型式可以得到精度足够、可资比较的结果，是合理可行的.

表2 几种抗滑桩的截面型式Tab.2 Several cross sections of anti－slide piles

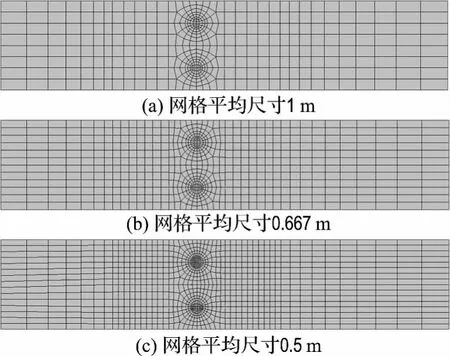
图3 不同网格密度下的模型底面(Z＝0)Fig.3 Bottom plane under different mesh densities(Z＝0)

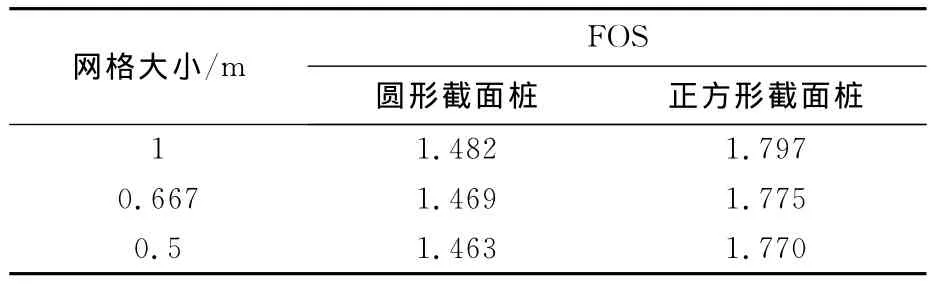
表3 不同大小网格下的安全系数(FOS)Tab.3 Factor of safety(FOS)under different meshes

2 计算结果与分析

针对前述的6种桩型抗滑桩－边坡体系，开展了桩头自由条件下体系的整体稳定性和桩身内力计算，所得安全系数列于表4，弯矩和剪力如图4所示.分析表4可见，T形、正方形、矩形、正五边形、正六边形、圆形6种截面桩加固边坡的安全系数逐渐减小，垂直于滑动方向的边长越大，所得安全系数越大，正方形与矩形两种截面很好地说明了这一点.实际上，对于这一现象并不难解释，在不考虑桩身塑性变形时，抗滑桩犹如不会破坏的障碍物，滑动土体遇到一堵不连续的挡土墙，土体的移动受到阻碍，墙面越宽，其阻滑能力越强，进而安全系数越大.

表4 不收敛时6种截面桩加固边坡的安全系数Tab.4 The FOS of six pile cross－sections at nonconvergence

图4 折减系数为1.35和1.50时桩身内力Fig.4 Internal forces along the piles as stress reduction factors are 1.35and 1.50

进一步地考察矩形截面桩(表2编号3工况)的加固效果，改变矩形截面桩的长、短边方向和长宽比a／b(其中a为矩形截面沿着滑动方向的边长，b为矩形截面垂直于滑动方向的边长)，所得结果列于表5；可见，a／b越小，即垂直于滑动方向的边长越大，则安全系数越高，与之前分析所得规律是一致的；但是，a／b越小，计算不收敛时桩身弯矩峰值越大(即桩承受的荷载越大)，桩身截面系数越小(即桩的抗弯能力越差).

表5 几种矩形截面桩加固边坡的安全系数和桩身弯矩峰值Tab.5 The FOS and the max bending moment along the piles under cases with different rectangle pile cross－sections

从上述分析可知，单从安全的角度考虑，显然T形截面最好，但是实际工程中往往需要考虑到施工的难易程度，因此，在滑动方向已知的情况下，往往选择安全性仅次于T形但施工简便的方形或矩形截面桩为好；但在滑动方向未知的情况下，圆形截面抗滑桩优于矩形截面桩.

图4给出了折减系数分别为1.35和1.50时6种不同截面桩的桩身弯矩和剪力分布图.分析可以得到如下结论:相同的折减系数下，桩的不同截面型式对桩身的内力分布几乎没有影响.这是因为桩间距一定时，土体产生作用于桩身的下滑力一定，故不考虑桩的塑性变化时，桩身的内力值是一致的.

从图4亦可发现，桩头以下10.5m附近桩身弯矩绝对值最大，这是因为此处是土体与岩石的分界处，而两者的弹性模量相差1 500倍，在该处产生巨大的差值，导致出现应力集中现象，进而影响桩身的弯矩分布.此外，从图4还可看出，当折减系数从1.35增加到1.50(增幅约11%)，沿着桩身的弯矩峰值和剪力峰值提高了60%左右；对T形截面桩，沿着桩身的弯矩峰值提高更多.由此得出结论，沿着桩身的内力峰值会随着折减系数的增加而增加，并且前者的增加幅度是后者的6倍.然而工程实际中的真实情况是，抗滑桩所能承受的荷载存在上限，当桩身的内力达到一定的范围时，将会发生塑性变形甚至破坏.故而，采用XTRACT[16]截面分析软件得到了圆形截面桩在不同配筋率下所能承受的极限弯矩值(为了便于研究，皆取圆形截面，其配筋均匀，所得极限弯矩具有参考性)，其结果列于表6.

表6 不同配筋率下桩身极限弯矩值Tab.6 Ultimate bending moments for different reinforcement ratios

实际工程中，抗滑桩的配筋率应在5%以下[17－18]，表6显示了圆形截面桩在不同配筋率下所能承受的极限弯矩值.从图4可看出，折减系数达到1.35时，沿着桩身的弯矩峰值已超过3×106N·m，这就要求抗滑桩的配筋率达到2%；折减系数达到1.50时，沿着桩身的弯矩峰值已到4.940×106N·m，这就要求抗滑桩的配筋率接近4%.然而，3%～4%的配筋率在实际中已经比较大，会导致经济成本的大幅抬高.因此，降低桩身的内力峰值是必要的.

图5显示了桩头采用固定约束时沿着圆形截面抗滑桩的内力分布情况.对比图4(自由桩头约束)可以发现，固定桩头能够有效地降低沿着桩身的内力峰值，并且沿着桩身的内力分布更加均匀.分析原因如下:将抗滑桩视作梁，桩底嵌入岩层中，相当于固定端，当桩头自由时，抗滑桩的变形和受力方式类似于悬臂梁，滑坡推力通过抗滑桩完全传递给下部稳定地层中；而桩头固定时，抗滑桩的变形和受力方式类似于两端固定的固端梁，滑坡推力部分通过抗滑桩传递给桩顶的约束，部分传递给下部稳定地层.因此，若桩头采用固定约束代替自由约束，则对于本算例中的圆形截面抗滑桩，只需要1%左右的配筋率就能满足实际受力的需要，大幅度地节约材料和降低经济成本.同样，若采用矩形或方形截面型式的抗滑桩，固定桩头在降低桩身位移和内力反应的同时，还可以一定程度上提高边坡的稳定性(表4).

图5 桩头固定时圆形截面桩的内力Fig.5 Internal force along pile under fixed mode

3 不同截面型式下桩间土拱效应

结合前文对不同截面型式下抗滑桩内力分析，本章对6种截面型式下抗滑桩桩间土拱的分布情况做进一步的探讨和研究.

图6给出了6种不同截面型式(T形、正方形、矩形、正五边形、正六边形、圆形)抗滑桩的工况下，计算不收敛时桩头以下4.0m处桩周土体的最大主压应力分布图.显然可以分为两组:左边3种工况下(图6(a)、(c)、(e))，桩间的应力拱棱角比较多，呈现多边形形状，分析原因是由于抗滑桩截面的棱角相对比较尖锐；右边3种工况下(图6(b)、(d)、(f))，桩间的应力拱则接近圆弧形，相对比较光滑；同一深度处，桩－边坡体系安全系数越大的截面工况，桩后应力集中程度越高；正如前文所述，6种工况下桩的截面型式不同但截面面积相同，当抗滑桩视作弹性体时，垂直于滑动方向并且迎向滑动方向的截面边长，对抗滑桩的加固效果影响相对较明显，这也是6种工况下截面形状为圆形时体系稳定性最差的原因.

图6 6种截面型式下桩间土拱分布Fig.6 Distribution of soil arching under six pile cross－sections

4 结 论

(1)等截面T形、正方形、矩形、正五边形、正六边形、圆形6种型式，所得安全系数逐渐减小.但实际工程中，在滑动方向已知情况下，矩形或方形截面桩优于T形截面桩；在滑动方向未知情况下，方形桩优于圆形截面桩.

(2)不考虑抗滑桩塑性变形时，抗滑桩犹如不会破坏的障碍物，滑动土体遇到一堵不连续的挡土墙，土体的移动受到阻碍，墙面越宽，其阻滑能力越强，进而安全系数越大.

(3)针对圆形截面桩，在桩头固定约束条件下抗滑桩配筋率1%以下就能满足受力要求，比桩头自由条件下可显著节省材料和降低经济成本，这也是工程中采用桩锚加固方案的原因所在.

(4)同一深度处，抗滑桩－边坡体系安全系数越大的截面工况，桩后应力集中程度越高；T形、正方形和矩形3种工况下，桩间应力拱呈多边形，而正五边形、正六边形和圆形截面桩的工况下，桩间土拱比较接近圆弧形状.

[1]中华人民共和国国土资源部.DZ 0240－2004滑坡防治工程设计与施工技术规范[S].北京:中国标准出版社，2006.Ministry of Land and Resource of the People′s Republic of China.DZ 0240－2004Landslide Control Engineering Design and Construction Technical Specifications [S]. Beijing:China Standard Press，2006.(in Chinese)

[2]年廷凯，栾茂田，杨 庆.考虑地震效应的阻滑桩加固土坡简化分析方法[J].大连理工大学学报，2007，47(5):718－722.NIAN Ting－kai，LUAN Mao－tian，YANG Qing.Simplified analytical procedure of stabilizing piles against sliding considering earthquake effect [J].Journal of Dalian University of Technology，2007，47(5):718－722.(in Chinese)

[3]徐海洋.考虑土拱效应的抗滑桩加固边坡数值分析[D].大连:大连理工大学，2012.XU Hai－yang. Numerical analysis of a slope reinforced with anti－slide piles considering soil arching effect [D].Dalian:Dalian University of Technology，2012.(in Chinese)

[4]Zienkiewicz O C，Humpheson C，Lewis R W.Associated and non－associated visco－plasticity and plasticity in soil mechanics [J].Geotechnique，1975，25(4):671－689.

[5]Griffiths D V，Lane P A.Slope stability analysis by finite elements [J].Geotechnique，1999，49(3):387－403.

[6]Griffiths D V，Marquez R M.Three－dimensional slope stability analysis by elasto－plastic finite element[J].Geotechnique，2007，57(6):537－546.

[7]Cai F，Ugai K.Numerical analysis of the stability of a slope reinforced with piles [J].Soils and Foundations，2000，40(1):73－84.

[8]张建华，谢 强，张照秀.抗滑桩结构的土拱效应及其数值模拟[J].岩石力学与工程学报，2004，23(4):699－703.ZHANG Jian－hua，XIE Qiang，ZHANG Zhao－xiu.Arching effect of anti－slide pile structure and its numerical simulation [J].Chinese Journal of Rock Mechanics and Engineering，2004，23(4):699－703.(in Chinese)

[9]Won J，You K，Jeong S，etal.Coupled effects in stability analysis of pile－slope systems [J].Computers and Geotechnics，2005，32(8):304－315.

[10]Wei W B，Cheng Y M.Strength reduction analysis for slope reinforced with one row of piles [J].Computers and Geotechnics，2009，36(7):1176－1185.

[11]高长胜，陈生水，杨守华，等.基于强度折减有限单元法的抗滑桩加固边坡特性分析[J].水利与建筑工程学报，2010，8(4):119－122.GAO Chang－sheng，CHEN Sheng－shui， YANG Shou－hua，etal. Analysis for slope stability reinforced with anti－slide piles based on strength reduction method with 3DFEM [J].Journal of Water Resources and Architectural Engineering，2010，8(4):119－122.(in Chinese)

[12]Liang R，Zeng S.Numerical study of soil arching mechanism in drilled shafts for slope stabilization[J].Soils and Foundations，2002，42(2):83－92.

[13]吕 庆，孙红月，尚岳全.抗滑桩桩后土拱形状及影响因素[J].哈尔滨工业大学学报，2010，42(4):629－633.LYU Qing，SUN Hong－yue，SHANG Yue－quan.Shape of soil arch behind anti－slide piles and its major influence factors [J].Journal of Harbin Institute of Technology，2010，42(4):629－633.(in Chinese)

[14]赵明华，廖彬彬，刘思思.基于拱效应的边坡抗滑桩桩间距计算[J].岩土力学，2010，31(4):1211－1216.ZHAO Ming－hua， LIAO Bin－bin， LIU Si－si.Calculation of anti－slide piles spacing based on soil arching effect[J].Rock and Soil Mechanics，2010，31(4):1211－1216.(in Chinese)

[15]Terzaghi K.Theoretical Soil Mechanics[M].New York:John Wiley and Sons，1943.

[16]Imbsen and Associates，Inc.XTRACT Ver.3.0.3[Z].Sacramento:Imbsen and Associates，Inc.，2000.

[17]中华人民共和国建设部.GB 50010—2002混凝土结构设计规范[S].北京:中国建筑工业出版社，2002.The Ministry of Construction of the People′s Republic of China.GB 50010—2002Design of Concrete Structures [S].Beijing:China Building Industry Press，2002.(in Chinese)

[18]中华人民共和国住房和城乡建设部.JGJ 94—2008建筑桩基技术规范[S]北京:中国建筑工业出版社，2008.The Ministry of Housing and Urban－Rural Construction of the People′s Republic of China.JGJ 94—2008Building Pile Technical Specifications[S].Beijing:China Building Industry Press，2008.(in Chinese)