基于自由度变动的几何公差分析模型

朱伟红 李恒亮

(河南省轻工业学校，河南郑州 450006)

计算机辅助公差(CAT)是计算机辅助设计/计算机辅助制造/计算机辅助检测(CAD/CAM/CAI)的数字化集成的关键环节之一。几何公差的数字化表达、分析、设计方法是CAT的理论基础。数字化的公差建模方法已经研究多年，其中比较有代表性的包括:漂移模 型［1］、参数化模型［2］、运动学模型［3］和自由度模型［4］。

本文根据新一代GPS的规定，在ASME － Y14.5.1M基础上，利用自由度变动模型阐述了几何公差的分析原理，并对若干具体的分析情况提出了计算流程。

1 公差与公差带数学模型

零件尺寸和几何参数的允许变动量称为“公差”。尺寸和公差的标准中，介绍了两种类型的公差:尺寸公差和几何公差，几何公差包括形状公差(如直线度、平面度、圆柱度等)、定向公差(如平行度、垂直度等)、定位公差(如位置度、同轴度等)和跳动公差(如圆跳动)等。

ASME于1994年颁布了尺寸和公差数学定义的标准14.5.1M［5］，以严格的数学形式来描述公差，其实质是用点集的矢量方程来定义公差带。公差带的4个要素是:形状、位置、方向和大小。在数学定义中，用中心要素(中心点、中心线、中心面)的位置矢量来确定公差带的位置，用中心要素的法矢量来确定公差带的方向，公差带的大小由用户给出，而公差带的形状可以由矢量方程直接确定。

公差的语义主要表示为以下两个方面:(1)公差带如何形成与表示。公差带是指允许尺寸、形状和位置变动的区域，在几何上表现为两个相距为公差值t的平面或一个直径为公差值t的圆柱等，因此存在怎样对此公差带进行定位、定向及求取其边界等问题;(2)变动后的要素如何形成及表示。变动后的要素在大小、形状和位置等各个方面均发生了变化，不再是以前的理想状态，因此存在怎样生成变动后要素的问题，即怎样在变动后的要素上体现出公差的效果，为自动公差分析、公差分配等后续工作生成变动实例。因此如何从数学的角度刻划出上述两个方面的公差语义对开发出一个完整的、正式的公差信息表示的数学模型是十分重要的。

公差的语义与定义是明确并且严谨的，正确的公差标注必须能够确定唯一一个明确的公差带，即公差带的4个要素必须完全并且唯一的确定。

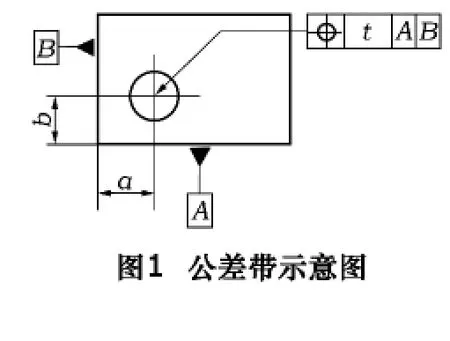
如图1中，两个理论正确尺寸a、b决定了公差带的位置和方向，参照的数目和形状决定了公差带的形状，公差值t决定了公差带的大小。

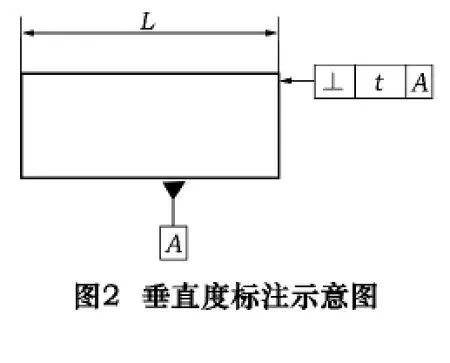
如图2中，尺寸L决定了公差带的位置，参照A决定了公差带的方向，特征的形状决定了公差带的形状，公差值t决定了公差带的大小。

也就是说，在明确施加公差的特征、施加的公差项目、公差参照以及公差值的条件下，公差带能够唯一确定，才是正确的公差标注，才能用以公差分析与综合。

2 基于自由度变动的几何公差表示方法

基于自由度变动的几何公差表示方法最早由Bourdet［6］在1996年引入到公差领域，是公差分析与综合的基础。其主要通过带有6个运动分量的刚体产生微小位移所构成的矢量表示。

产品规范设计中，设想的实际表面是一偏离名义表面的理想表面，零件几何特性可由特征表面的法线方向和点表述。特征的变动量可以用6个矢量精确地表示:3个平动矢量和3个旋转矢量，如公式(1)所示。

通常，尺寸公差与几何公差是通过公差带进行描述的，公差带表达了实际特征偏离名义位置的变动的范围。传统上，公差带主要通过图形语言进行描述。公差数学建模的主要目的就是要通过数字化方法描述公差带。基于自由度变动的几何公差表示方法中，6个参量的变动范围和约束关系可以完整的表达实际特征相对于名义位置的变动范围，即公差带。

因分析对象通常只有平面特征与圆柱特征，故只针对这两种特征给出其几何公差的参数化表示方法。

2.1 平面特征几何公差表示方法

平面特征具有如表1所示的几何公差项目［7］。

由于平面特征的形状、定向、定位和端面全跳动公差带在数学上有统一的表达方法，公差带的形状也是一致的，则基于自由度变动的公差带表达方法也相对统一。

表1 平面特征几何公差项目公差带形状示意

对于平面特征，拥有3个自由度，其变动矢量［8］如公式(2)所示。

平面特征的公差带是由两个位于公差极限的平面所包容的区域，如图3所示。

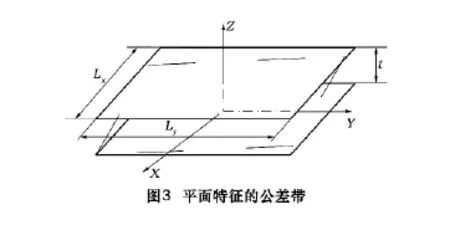
则可以得到变动矢量的变动范围和约束条如公式(3)所示［8］:

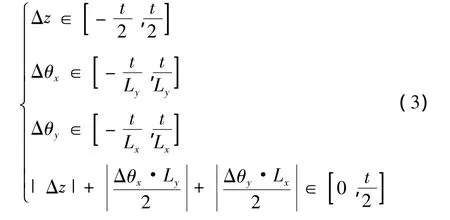
2.2 圆柱特征几何公差表示方法

圆柱特征具有如表2所示的公差项目［7］。

表2 圆柱特征几何公差项目公差带形状示意

对于圆柱特征，圆柱型公差带的数学表达为

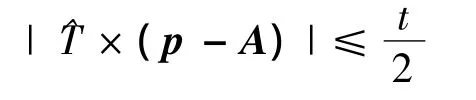
公差带是两同心圆之间的区域的数学表达为

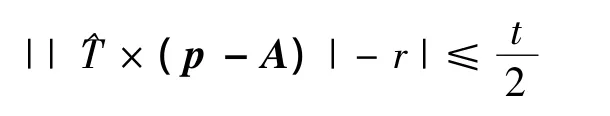
公差带是两同心圆柱之间的区域的数学表达为

以上3种公差带的自由度变动参数如下［8］:

圆柱型公差带的自由度变动参数公式为

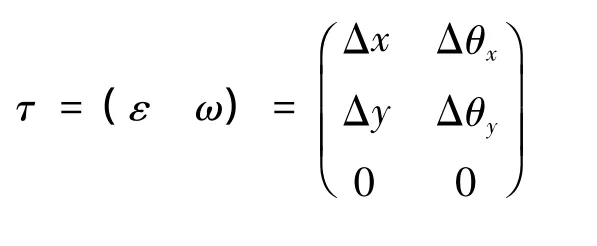
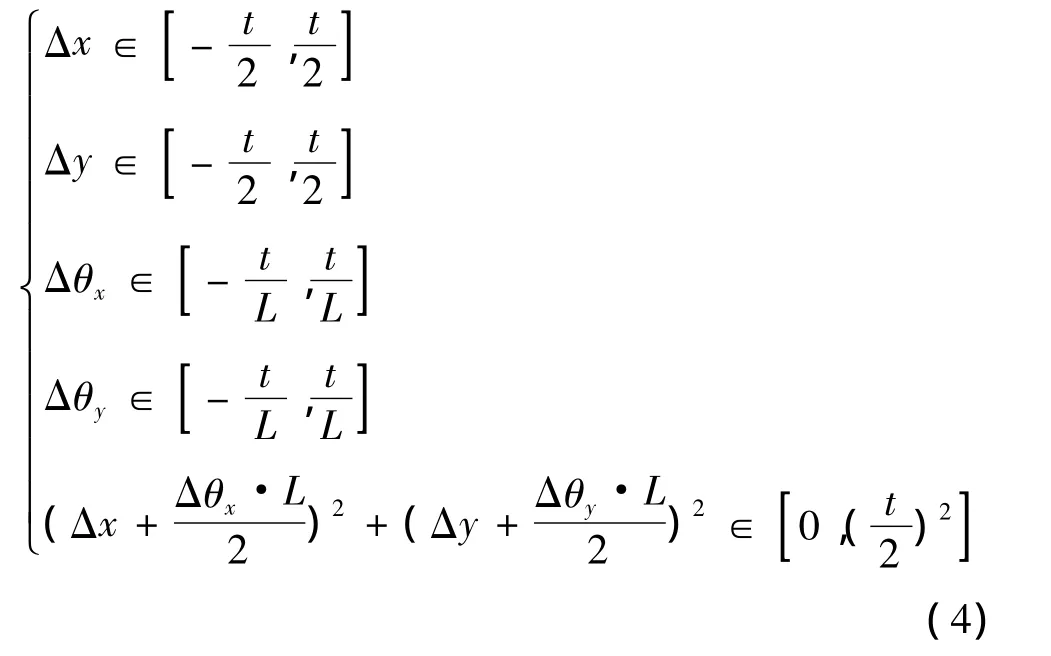
两同心圆型公差带的自由度变动参数公式为

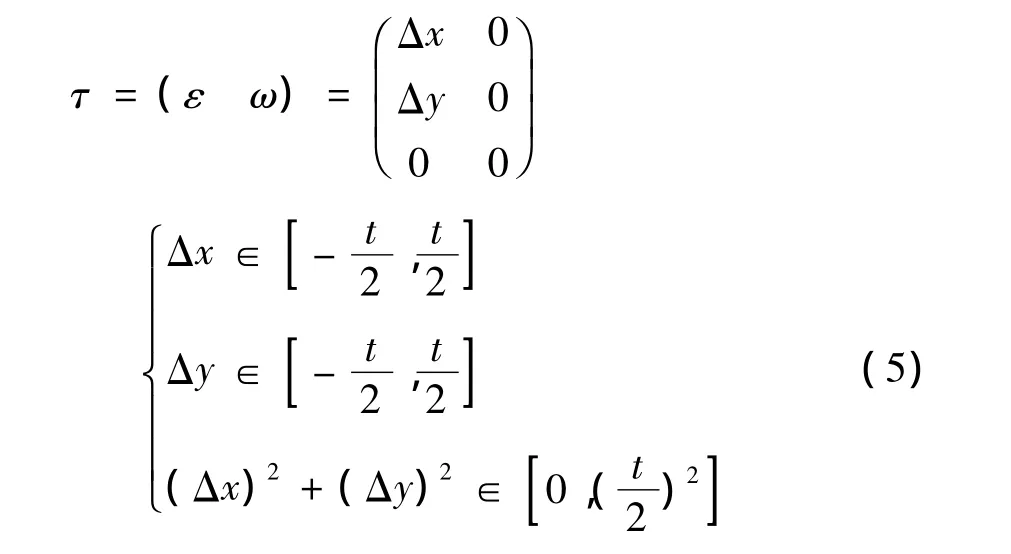
两同心圆柱型公差带的自由度变动参数公式为

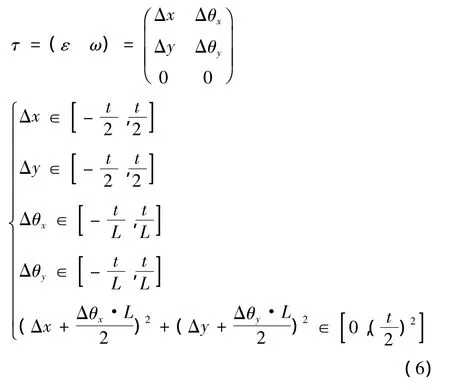
3 基于自由度变动的多公差综合参数化表达方法

3.1 对于同一特征多种几何公差共同作用下的自由度变动参数表达方法

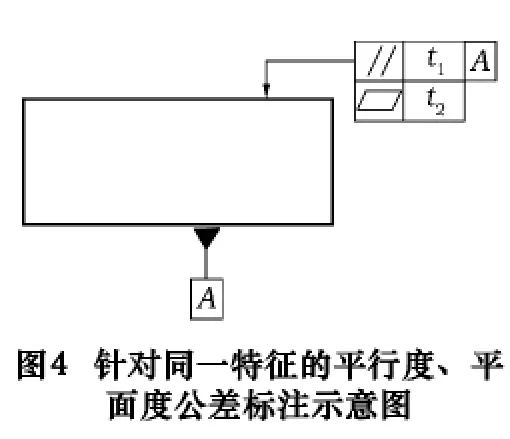
在设计实践中，常常会对同一特征给出多种几何公差，图4中给出了一个例子。

正确的公差语义应当是具有唯一解释的，那么通过确定自由度变动参数的变动范围，应当能够表达出唯一一个具有确定的空间位置、方向、形状与大小的公差带。

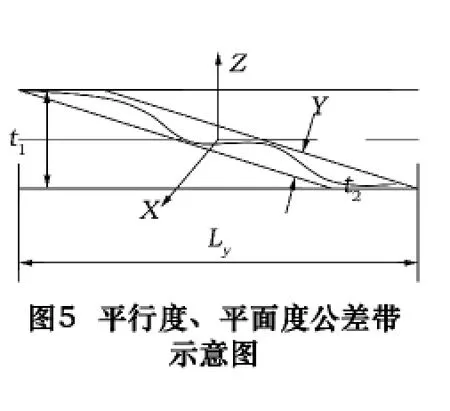
对于定位或者定向公差与形状公差(如图5所示)共同作用于同一特征时，可以推出其误差的控制边界公式为

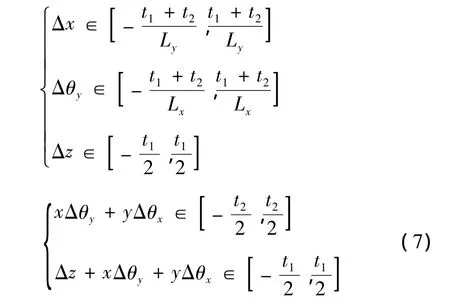
将计算这两种误差叠加的运算定义一个运算符号为⊕，则

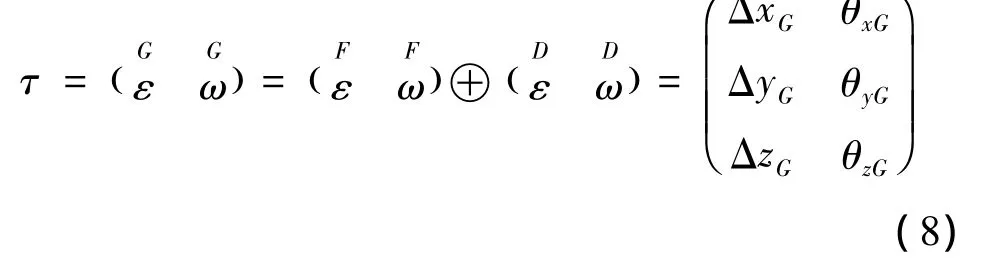
3.2 对于基准存在误差的特征的几何公差自由度变动参数表达方法

对于定向公差、定位公差等有基准的公差项目，为了保证装配完成之后，目标特征的空间位置姿态符合设计要求，必须考虑基准存在误差的情况。

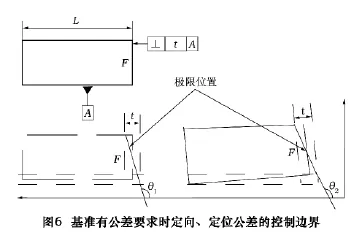
例如，在设计时，为某零件的设计如图6所示的公差。

假设基准A存在公差，其对应的公差带如图6所示。由于基准存在误差，虽然F面相对于基准A的垂直度公差未超差，但是其空间姿态θ2和设计时的空间姿态θ1相比已经发生了变化，即A的误差已经影响了F面的空间位姿参数。

对于这种误差引起的目标特征的空间位姿参数的变动，可以通过以下公式计算:

假设在零件坐标系下，F面相对于基准A的旋转变换矩阵为，位移变换向量为;若基准A为平面特征，则其公差带可以表述为

则F面的空间位姿变动为

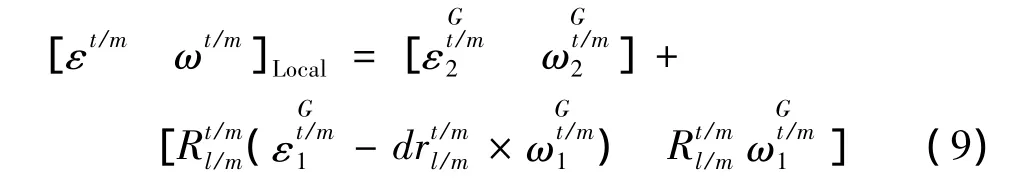
3.3 形状公差在装配公差分析中的处理方法

形状公差(包括平面度、直线度、圆度与圆柱度)对于装配公差图的影响可以概括为以下4种情况:

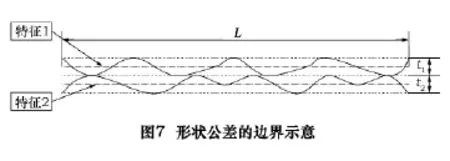
(1)当只规定有形状公差的两个特征配合时，若配合平面的尺度远远大于形状公差(一般情况下均为此)，仍可以将配合表面视为理想形状。

传递至目标特征的误差如公式为

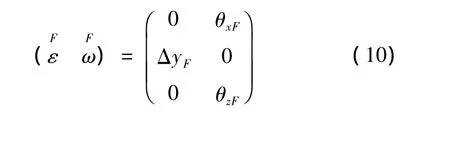
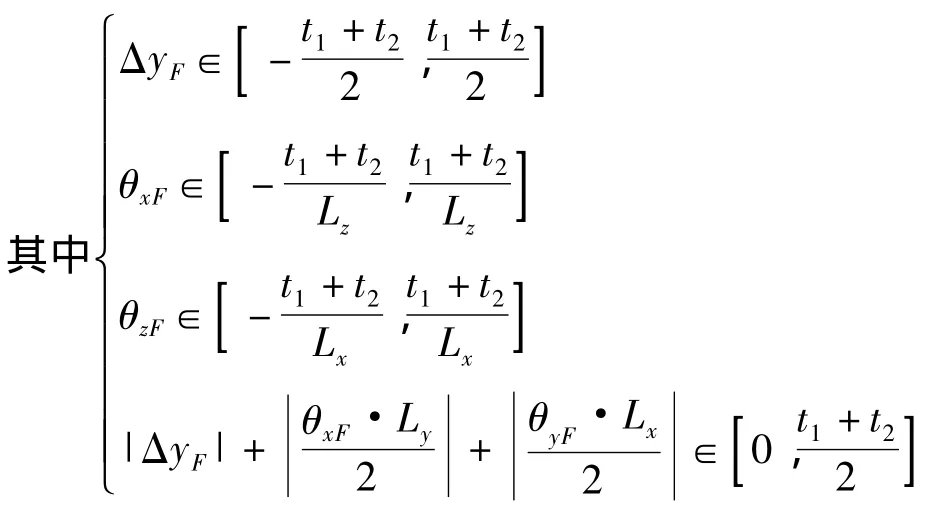
(2)当特征既规定了形状公差，也规定了尺寸公差或者定向公差时，由于定向公差一般大于形位公差，在配合特征尺度远大于公差t时，将配合表面视为理想表面。

(3)当配合特征的尺度与公差t接近时(通常指点接触)，需要考虑形状公差。

此时，要考虑特征上每个位置可能出现的误差。

以平面度为例，若平面度的自由度参数表达为

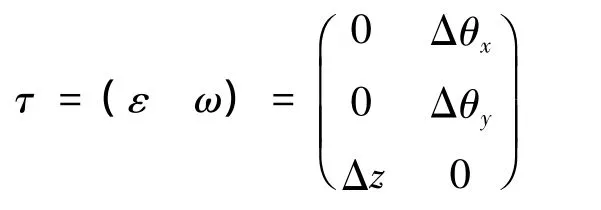
平面上任意一点(x，y)应当满足的约束条件为

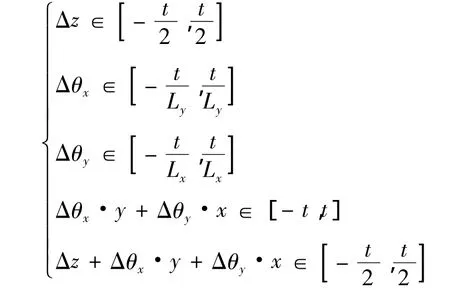
此时，在计算装配公差时，应当将装配点的形状公差计算在内。

4 基于自由度变动的几何误差传递与积累计算模型

通过以上的分析，有多种误差影响一个特征的空间位姿，包括:尺寸误差，本特征的几何误差，基准的几何误差。

对于装配体目标特征(GTF)的空间位姿，应采用几何误差传递与积累计算模型，如图8所示，应当采取以下分析步骤:

步骤1:将所有公差转化为基于自由度变动的矢量参数。

步骤2:从基准出发，计算零件1目标特征(LTF)的空间位姿。

步骤3:假设零件1的LTF与零件2的基准CF1配合，将零件1的LTF的误差作为零件2的基准的几何误差，重复步骤2，计算零件2的LTF的空间位姿。

重复步骤2、步骤3，直到计算出GTF的空间位姿变动参数。

5 结语

本文首先阐述了公差数字化分析的基本理论和原理，然后提出了同一特征多种公差要求、基准存在误差的公差要求和形状公差数字化分析的具体分析方法，最后提出了空间误差累积的计算流程。

［1］Allada V，Huffer N，Anand S.Quad and octree structures for tolerance representation in solid models［C］.//In Proceedings of 2ndIndustrial Engineering Research Conference.Lops Angeles，1993:461 －465.

［2］Krishna KK，Osama K E，Jin B.Modeling of manufacturing processes characteristics for automatted tolerance analysis［J］.Ingernational journal of industrial engineering，1997，4(3):187 －196.

［3］Rivest L，Fortin C，Morel C.Tolerancing asolid model with a kinematic formulation［J］.Computer－ aided Design，1994，26(6):456 －476.

［4］Kandikjan T，Shah J J，Davidson J k，A mechanism for validating dimensioning and tolerancing schemes in CAD systems［J］.Computer －aided Design，2011，33(10):721 －737.

［5］American Society of Mechanical Engineers.Mathematical definition of dimensioning and tolerancing principles［S］.ASME/ANSI Standard Y14.5.1M －94，New York NY，1994.

［6］Bourdet P，Mathieu L，Lartigue C，Ballu A(1996)the concept of the small displacement torsor in metrology［S］.Adv Math Tools Metrol 40:110－122.

［7］中华人民共和国国家标准.GB/T 1958－2004，产品几何量技术规范(GPS)形状和位置公差检测规定［S］.北京:中国标准出版社，2005.

［8］蔡敏，杨将新，吴昭同，基于数学定义的圆柱要素形状公差数学模型的研究［J］，机械工程学报，2003，39(12):86 －90.