回转误差测试中主轴旋转方向与传感器相互位置关系的判定研究*

2013-09-27马晓波刘启伟张耀满

制造技术与机床 2013年8期

马晓波刘启伟张耀满

(①沈阳机床(集团)有限责任公司高档数控机床国家重点实验室，辽宁沈阳 110142;②东北大学机械工程与自动化学院，辽宁沈阳 110004)

机床主轴回转误差运动是指在主轴回转过程中回转轴线偏离理想轴线位置而出现的附加运动，是影响机床加工精度的主要因素，是衡量机械系统性能、评价机床动态特性的一项重要指标［1－2］。造成机床主轴回转误差的原因有主轴传动系统的几何误差、传动轴偏心、惯性力变形、热变形等误差，也包括许多随机误差。

通过径向跳动量和轴向窜动量测试实验可以有效地满足对回转精度测量的要求，对测试数据的进一步分析，则是了解回转轴的运动状态和判断产生误差运动原因的必要手段。在主轴回转误差分析中，主轴的旋转方向与径向上两个位移传感器的位置关系往往被忽略，即使考虑到这一因素一般也是采用人工记录的方式，其可靠性和便利性受到一定的影响，对测试数据的后续分析处理带来了很多不便。

本文在对主轴回转误差测试模型分析的基础上，探讨了一种自动分析判定主轴旋转方向与径向传感器位置相互关系的方法，经过适当简化得到了很好的应用效果。

1 旋转方向对回转误差的影响分析

理想的机床主轴只有一个旋转自由度，沿其他方向的运动均被视为误差运动或对外部作用的反馈行为［3－4］。回转误差运动一般可以分为3种基本形式:(1)与回转轴线平行的径向位移(纯径向跳动);(2)与回转轴线平行的轴向位移(纯轴向窜动);(3)倾斜(纯角度摆动)。

一般情况下，这3种基本形式的误差是同时存在的，产生的加工误差也是这3种形式误差影响的叠加。

径向误差的大小取决于测量头的轴向位置，轴向误差的大小取决于测量头在测量平面上的径向位置。因此应尽量减小安装误差以提高测试精度。一般主轴的径向回转误差采用如图1所示的测试仪器。

对于一组测试数据，主轴的旋转方向不会影响分析的数值结果，如同步误差、非同步误差和总误差等，但会影响误差的图形特性。图2是同一测试数据考虑主轴旋转方向后径向同步误差的分析结果，图2a认为主轴顺时针旋转，图2b认为主轴逆时针旋转。可见，在考虑主轴回转方向后，在主轴起始角度不为零的情况下，主轴径向回转误差的分析结果虽然形状不变，但相位角却发生了变化，在精确分析和误差溯源中这是值得考虑的因素。

2 旋转方向的判定

为了简化分析模型，首先以主轴只具有安装偏心情况为例，分析回转误差测试结果。设主轴安装偏心量为a、b，测试心棒半径为r，测试示意图如图3所示。

其中:O为理想主轴中心位置;O′为安装偏心位置;α为起始角，主轴初始位置时OO′与X轴的夹角;S1、S2为位移传感器。

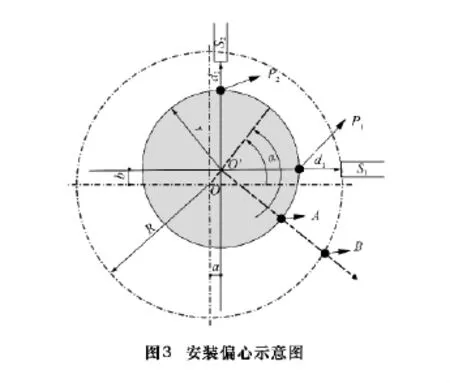
主轴逆时针旋转时，相当于主轴不动传感器S1和S2以O为圆心作顺时针旋转;主轴顺时针旋转时，相当于主轴不动传感器S1和S2以O为圆心作逆时针旋转。现以S1传感器为例，图中虚线外圆为S1传感器相对于主轴的相对运动轨迹，其测量结果即为以O′为起点的射线与虚线外圆和主轴外圆的交点间的距离，即AB线段长度。

以O′为圆心，主轴外圆和虚线外圆的直角坐标方程分别为:

将式(1)、(2)变换为极坐标方程分别为:

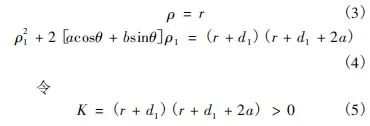
由式(4)求得:

对上式求导，得

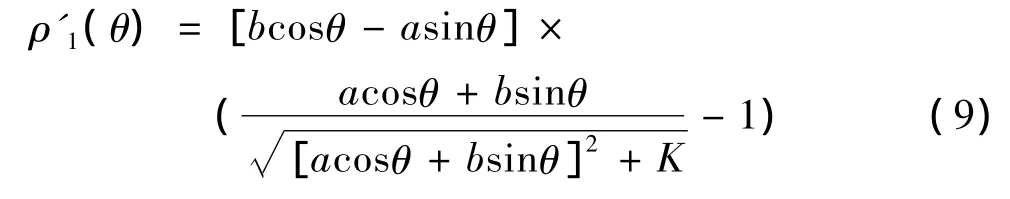
考虑公式(5)，所以在式(9)中，有

即式(9)的符号与K无关，也就是与d1无关。

令S1传感器测量结果所形成的曲线为S1曲线，S2传感器测量结果所形成的曲线为S2曲线。则S1曲线的单调区间判别函数可简化为:

同法，可以求得S2曲线的单调区间判别函数。另外，S1和S2传感器的安装位置相差90°，因而可以很容易得到S2曲线的单调区间判别函数。当主轴顺时针旋转时，传感器S2的单调区间判别函数为

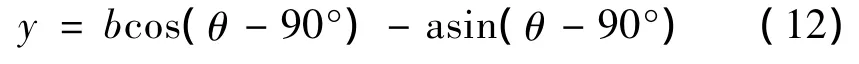
当主轴逆时针旋转时，传感器S2的单调区间判别函数为

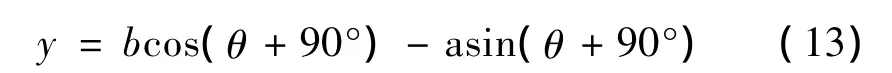
根据式(11)、(12)和(13)，以 45°为一个区间，将主轴一个回转周期分为8个区域，计算3条曲线的单调区间，计算结果见表1示。

由于测试过程的连续性，表1中的角度是一个从0到360°的往复过程，因此从表1可以提取出表2所示连续数据。

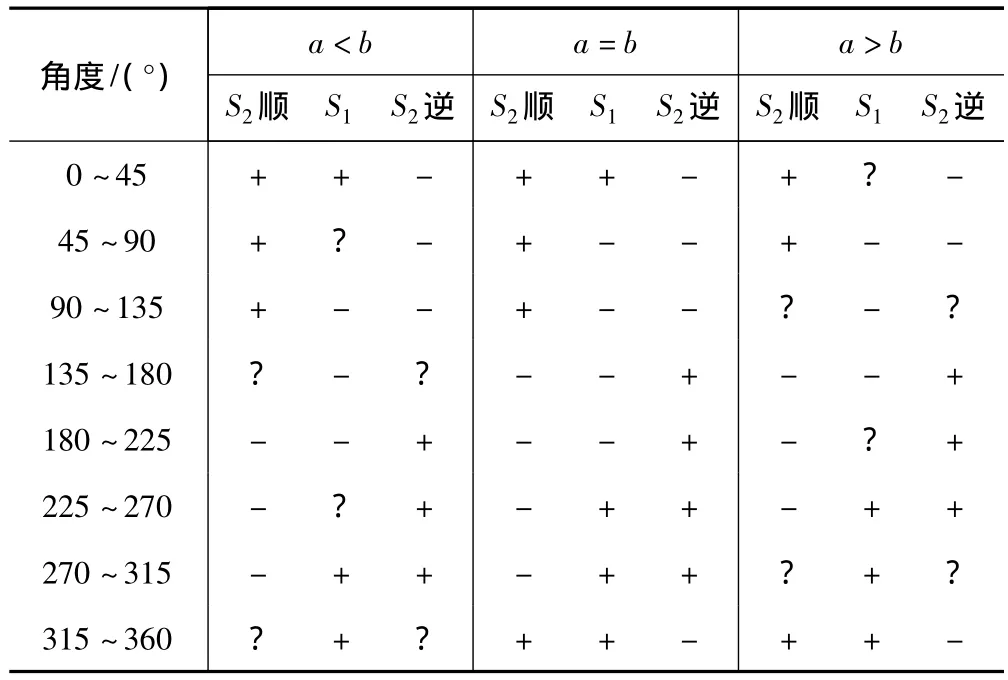
表1 曲线单调区间

从表2可以归纳出如下结论:

无论a、b大小关系如何，主轴顺时针旋转时，当S1曲线和S2曲线都进入单调递增区间后，S1曲线先进入单调递减区间;主轴逆时针旋转时，当S1曲线和S2曲线都进入单调递增区间后，S2曲线先进入单调递减区间。

以上推导过程假设主轴检棒没有圆度误差，但考虑到在实际的测试中使用高精度的球头检棒，一般地，相对于主轴的回转误差来说其圆度误差可以忽略不计，因而以上推导过程是成立的。

表2 关键数据点

在主轴回转误差的3种基本形式中，主轴的轴向窜动对上述分析没有影响，而主轴的安装倾角理论上只是增大主轴的回转半径，因此以上结论同样适合于主轴有安装倾角以及不同形式误差的叠加状态。

据此，可以通过主轴回转误差测试中两个径向位移传感器测量结果的单调性变动情况来判定主轴的回转方向。

3 试验验证

由于a、b变量的存在，以及a、b变量随主轴旋转位置的变动而产生变化的情况，直接通过判别函数式(11)、(12)或(13)来判断主轴的旋转方向是不可能的，因此在实际的应用中采用适合计算机处理的方法。首先将S1和S2曲线展开，然后画一条与S1和S2曲线都相交的直线，一般取S1曲线的算术平均值或有效值作为直线的初始值，如图4所示。

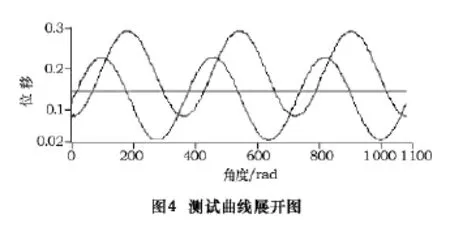
从起点出发，沿曲线向右移动，当两条曲线都位于直线上方时，令先下降与直线相交的曲线所对应的传感器为Sa传感器，另一个为Sb传感器，则主轴旋转方向为Sa经劣弧至Sb。若直线只和其中一个相交时，可以上下平移直线，直到满足要求为止。

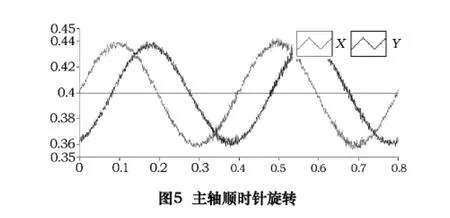
图5和图6是同一次主轴回转误差测试中在1 500 r/min时主轴正反转的测试结果，测试过程中主轴径向传感器的位置始终保持不变。根据本文提出的旋转方向的判定准则，图5中主轴旋转方向为由X向Y，而图6中主轴的旋转方向为由Y至X，分析结果与实际的主轴旋转方向一致。

在实际应用中，由于测试仪器的安装误差和噪声等干扰信号的存在［5］，在分析主轴旋转方向前可对测量数据进行低通滤波或平滑处理。同时，在对比数据时需要设定一个阈值，当对比状态连续次数超过阈值时，才能认为此状态是有效的，以提高判定的稳定性。为了验证以上分析结果，编制了主轴回转误差分析程序，流程图如图7所示。