压力矫直厚壁钢管的载荷-挠度模型研究
2013-09-26马更生田雅琴王海澜
马更生,田雅琴,王海澜
(太原科技大学,太原 030024)
钢管在轧制或热处理后,因受到外力、热应力或组织应力的影响,从而产生弯曲变形。对于钢管端部和大直径钢管的弯曲变形,常用压力矫直[1]。计算钢管矫直行程是钢管自动矫直机的关键技术。基于矫直曲率方程[2]的矫直模型计算必须依据零件轴线拟合出曲线方程,该曲线方程存在多点测量误差和人为拟合误差,计算精度受到影响,应用也不方便。文献[1,3]使用有限元的方法对计算钢管矫直行程进行了研究,所需的时间较长,且没有很好地反映钢管压力矫直过程的变形机理。文献[4]的理论研究中将弹区比假设为定值,且没有考虑截面的塑性压扁,因而产生较大误差。文献[5]提出了载荷-挠度模型,且证明了该模型具有较高精度,但是该文中未给出针对变形较为复杂的厚壁钢管的模型。针对目前计算压力矫直厚壁钢管行程精度低,通常需要重复矫直,效率低下等问题,笔者依据弹塑性理论,建立了能用于压力矫直厚壁钢管过程中的载荷-挠度模型,反映了压力矫直厚壁钢管的变形机理,此模型考虑了截面塑性压扁。
1 弹性阶段的载荷-挠度模型

钢管在弹性弯曲时挠度与载荷的关系为:

2 弹塑性阶段的载荷-挠度模型
压力矫直厚壁钢管时弯矩的分布为:

当钢管发生塑性变形时,钢管中间截面的塑性变形分为没有深入到内径和深入到内径2种情况。由于这2种情况的弯矩与弹区比的关系不同,弹区比为弹性层高度与截面高度的比值,故需要分类讨论。
当塑性变形没有深入到内径时,即 a<ζ1<1时,如图1所示。
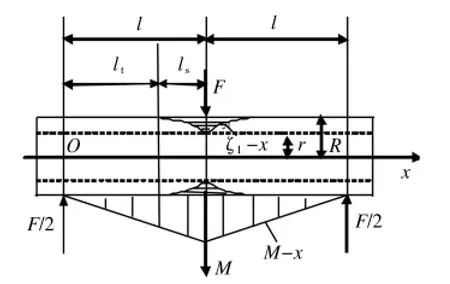
图1 未深入到内径的塑性变形区分布Plastic deformation distribution outside inner diameter
厚壁钢管弹塑性变形区内的弯矩计算公式为:

式中:σs为钢管的屈服应力。
当a=0.8时,管材的弹性极限弯矩为:
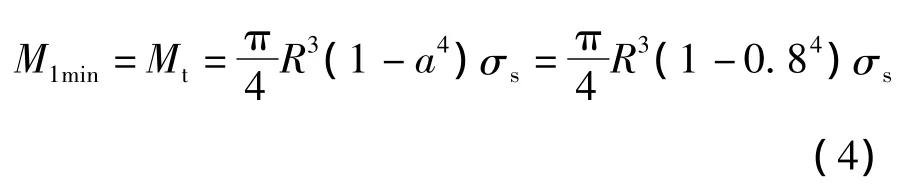
即当ζ1=0.8时,得此种情况下的极限弹塑性弯矩为:

在弹塑性区内,截面弯矩可以由式(1)或者式(2)计算,联立求解两式,可得x-ζ1的关系:

由式(8)—(12)可得厚壁钢管在弹塑性变形阶段的载荷-挠度模型为:

当塑性变形深入到内径时,为了避免压力矫直时厚壁钢管受到塑性压扁而出现畸变,只考虑中间截面的弹区比在a-0.1<ζ1<a时的情况,如图2所示。塑性层长度ls=ls1+ls2,其中ls1为当ζ1从1变化到a时,x相应变化的长度,此种情况的x-ζ1关系如式(8)。
厚壁钢管弹塑性变形区内的弯矩计算公式为:


图2 深入到内径时塑性变形区分布Fig.2 Plastic deformation distribution into the inner diameter
式中:Mt1为粗棒的弹性极限弯矩
当ζ12=a时,管材的弯矩为:
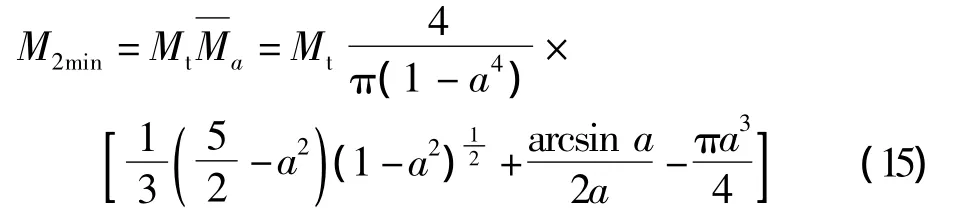
当 ζ12=a -0.1=0.7 时,得此种情况下的极限弹塑性弯矩为:

在弹塑性区内,联立求解式(1)和式(8),可得x-ζ12关系:


3 有限元及实验验证
通过有限元方法及实验验证压力矫直厚壁钢管的载荷-挠度模型。
厚壁钢管的压力矫直是材料非线性的弹塑性问题,文中采用有限元软件Ansys进行厚壁钢管的压力矫直分析。单元选用BEAM188,此种单元提供强大的非线性功能。该例中钢管材料选用45号钢,简化为理想弹塑性材料,弹性模量E为210 GPa,泊松比为0.3,屈服极限σs为355 MPa。截面选择圆环,外半径为50 mm,内半径为40 mm。通过创建关键点连接成直线,构成钢管的几何模型,钢管长度为1000 mm,将其划分为500个单元。根据简支梁的约束条件对钢管两端施加约束,支点距为1000 mm。压力矫直厚壁钢管载荷-挠度模型的计算结果与有限元模型计算结果见表1,图3和图4给出了表1中的关键参数弹区比、挠度和压下力之间的关系。
1)压力矫直厚壁钢管载荷-挠度模型的计算结果与有限元模型计算结果对比,整体趋势一致,误差较小,最大值为2.9%,说明所建立的载荷-挠度数学模型具有较高的精度、正确性和准确性。

表1 载荷-挠度模型与有限元及实验结果对比Table1 The comparison between model,finite element model and experimental results

图3 弹区比-挠度曲线Fig.3 ζ-δ curve
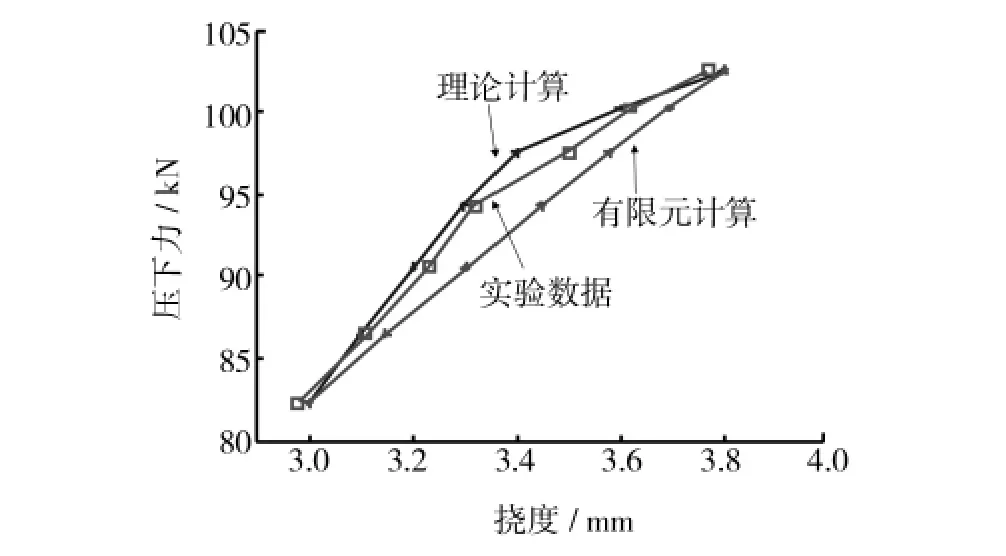
图4 挠度-压下力曲线Fig.4 δ-F curve
2)将有限元模拟的数据和实验数据对比发现,整体趋势一致,误差较小,最大值为4%,证明应用有限元方法分析压力矫直厚壁钢管可行。
4 结语
1)依据弹塑性理论,在对理想弹塑性材料的厚壁钢管进行压力矫直时,考虑其弹塑性弯曲阶段的变形可以分为2种情况,即塑性变形是否深入到内径,分别给出了此2种情况的载荷-挠度数学模型的表达式,最后模拟对照验证了该模型具有较高的一致性。
2)文中只给出了压力矫直理想塑性材料厚壁钢管的载荷-挠度数学模型表达式,具有一定的局限性,若考虑弹塑性材料厚壁钢管的加工硬化,可以使误差减小。
[1]王志飞,田雅琴,黄庆学,等.基于LS-DYNA压力矫直钢管反弯挠度的计算[J].重型机械,2010(6):62-64,68.
[2]崔甫.矫直原理与矫直机械[M].北京:冶金工业出版社,2007:83-94.
[3]李瑞斌,毛春燕.钢管压力矫直过程有限元分析[J].锻压装备与制造技术,2011,46(3):60-62.
[4]高展,刘春旭,朱世忠,等.钢管压力矫直行程计算公式的理论研究[J].宝钢技术,2009(1):52 -55.
[5]李骏.基于校直过程模型的校直工艺理论及实验研究[D].上海:上海交通大学,2005.
[6]陈慧,熊国良,李骏,等.基于F-δ模型的校直压下量确定方法及应用[J].机械设计与研究,2005,21(4):70-73.
