AP/HTPB推进剂扩散火焰结构分析①

叶 锐，余永刚，曹永杰

(南京理工大学能源与动力工程学院，南京 210094)

0 引言

复合固体推进剂在火箭推进领域成为研究热点已超过50年，20世纪60～70年代期间，主要在复合推进剂燃烧特性和理论建模方面进行了广泛的研究，致力解决燃速－压力关系;在其后的15年间，研究步入一个相对低迷期，紧接着由于实验诊断技术和数值模拟的发展，复合固体推进剂的研究又逐渐兴起。AP/HTPB复合固体推进剂燃烧时，出现复杂的多火焰结构，在实际火箭发动机燃烧室中，由于该火焰的微观几何特性，使得研究该火焰结构非常困难。直到1986年，Price［1］采用三明治推进剂(氧化剂/燃料/氧化剂)结构布置后，才使得研究该火焰结构成为可能。复合固体推进剂燃烧过程中，出现明显的扩散火焰，在燃烧表面附近，由于温度较低，扩散火焰不能一直延伸到推进剂表面，因此出现火焰前沿;在火焰前沿与推进剂表面之间，氧化剂和粘合剂分解气体发生掺混，所以前沿结构也表现出部分预混特性，Price称该结构为前沿火焰结构(leading－edge－flame，LEF)。其后，由于实验诊断技术的发展，使得观察该火焰结构成为可能。Chorpening等［2］、Ramakrishna 等［3］通过高速摄影的方式，观察到前沿火焰结构的分离情况，该结构对燃烧表面轮廓有较大影响。Fitzgerald等［4－5］通过紫外发射和透射成像技术讨论了不同条件下前沿火焰结构合并、分离情况，并给出了其合并、分离区域及过渡转变的临界条件。

本文以三明治结构布置，针对复合固体推进剂扩散火焰结构，研究了Pe数和Da对前沿火焰结构的影响，对认识复合固体推进剂燃烧有参考价值。

1 物理模型

AP/HTPB固体推进剂燃烧二维三明治模型如图1所示，仅针对复合固体推进剂燃烧表面上方的扩散火焰结构，未考虑燃面与气相之间的耦合，假设燃烧表面为平面，界面处质量流量为常数，氧化剂和粘合剂在燃烧表面处分解为氧化性气体X和粘合剂产物Y，气相成分只考虑组分X、Y和燃烧产物P，化学效应只考虑与扩散火焰结构相关的一阶有限速率化学反应;气相密度为常数，故忽略气体状态方程;气相区域采用Ossen［6］近似，认为只存在竖直方向的速度分量，消除动量方程;在气相中，Le=1;在实际的固体火箭发动机工作条件下，对流速率和组分输运速率在一个量级［7］，燃烧表面处的边界条件由传统的Dirichlet边界条件变为流量边界条件。

2 数学模型

2.1 控制方程

采用如图1所示坐标系，组分方程和能量方程为

式中 M为沿y方向的质量流量;ρ为气相密度;D为二元扩散系数;cp为气体比定压热容;λ为气体热导率;αX、αY为基于质量的化学计量系数;Ω为化学反应源项;Q为化学反应热释放总量。

2.2 气相化学动力学

AP一步分解反应生成氧化性气体混合物X［8］，X为:1.62H2O+1.105O2+0.265N2+0.12N2O+0.23NO+0.76HCl+0.12Cl2。

当AP/HTPB复合固体推进剂燃烧时，由于AP独特的物化特性，使得AP单元火焰主要在集中在AP表面上方，作用是维持AP自持分解，厚度仅为几个微米。因此，在某种程度上，可把AP单元火焰当做凝聚相表面反应［9］。在实际的火箭发动机工作环境下，Gordon和McBride［10］验证了AP/HTPB的气相化学反应可等效为AP/C2H4的气相反应过程，故HTPB的分解产物Y为C2H4。因此，氧化剂AP在燃烧表面处分解产生氧化性气体混合物X，粘合剂HTPB在燃烧表面出分解产生C2H4，AP/HTPB的气相化学反应简化为X和Y的扩散化学反应。

式中 B′为指前因子;p为燃烧压强;n为燃烧压强指数;E为活化能;R为普适气体常数。

为讨论方便，将压力项包含在指前因子中B=B′pn。

2.3 边界条件

2.4 无量纲化

作无量纲变换:

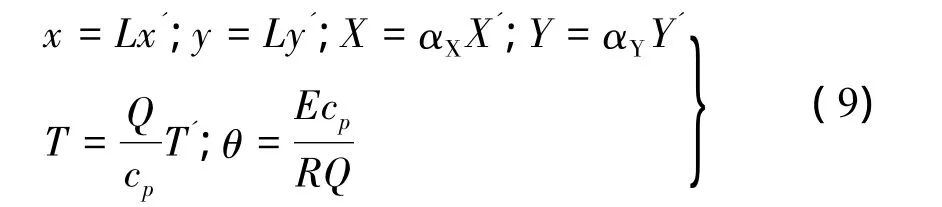
同时，引入贝克莱数Pe=ML/ρD和达姆科勒数Da=BLαXαY/M，Pe表征对流速率与组分输运速率的相对大小，Da表征无量纲化学反应速率大小，那么方程组变为

2.5 参数取值

对AP/HTPB复合固体推进剂，氧化剂蒸气与粘合剂蒸气化学计量比β一般在7左右，满足化学计量配比时，粘合剂含量为α=1/(1+β);Pe的变化范围是0.5～20，Da 的量级大致为 0.1e20，可取 Da=δe20;αX、αY为化学计量参数，其比值满足αX/αY=β即可。假设无量纲绝热火焰温度按Burke－Schumann扩散火焰面温度给出:

本文计算过程中，β=7，δ=0.1～0.5，Ta=1，Tw=1/3，1/αX=16/21，1/αY=16/7。

3 结果分析

3.1 Schvab-Zeldovich 分析

引入 Shvab－Zeldovich 变量 Z= αX(X′－ Y′)，按Burke－Schumann同轴射流扩散火焰理论，在火焰面处，组分X、Y将变为零，即Z=0，那么Z=0可称为化学计量表面(stoichiometric level surface，SLS)，或称为虚拟扩散火焰面，其位置由式(14)求得:

该边界条件为流量边界条件，即考虑了Pe数较小时，对流输运速率与组分扩散速率在相同量级时，来流质量流量等于对流输运质量流量与扩散输运质量流量之和，化学计量表面SLS与推进剂表面的交点在氧化剂与粘合剂交界面处偏向氧化剂侧，见图2。

该偏移将随着Pe数的增大而逐渐趋近于氧化剂和粘合剂交界面|x|=0.125处。假设当Pe→∞时，式(15)的边界条件变将为Dirichlet边界条件，即

采用流量边界条件与Dirichlet边界条件的主要区别在于燃烧表面处的Z值是否连续。当采用Dirichlet边界条件时，在氧化剂和粘合剂交界面处，Z值由1阶跃变化到－β，而流量边界条件则连续，如图3所示。当采用流量边界条件时，Z=0在|x|=0.26处，偏离氧化剂和粘合剂交界面|x|=0.125;当采用Dirichlet边界条件时，从Z值分布可看出，氧化剂不能出现在粘合剂侧，粘合剂不也能出现在氧化剂侧，该结果与实际条件不相符［11－12］。

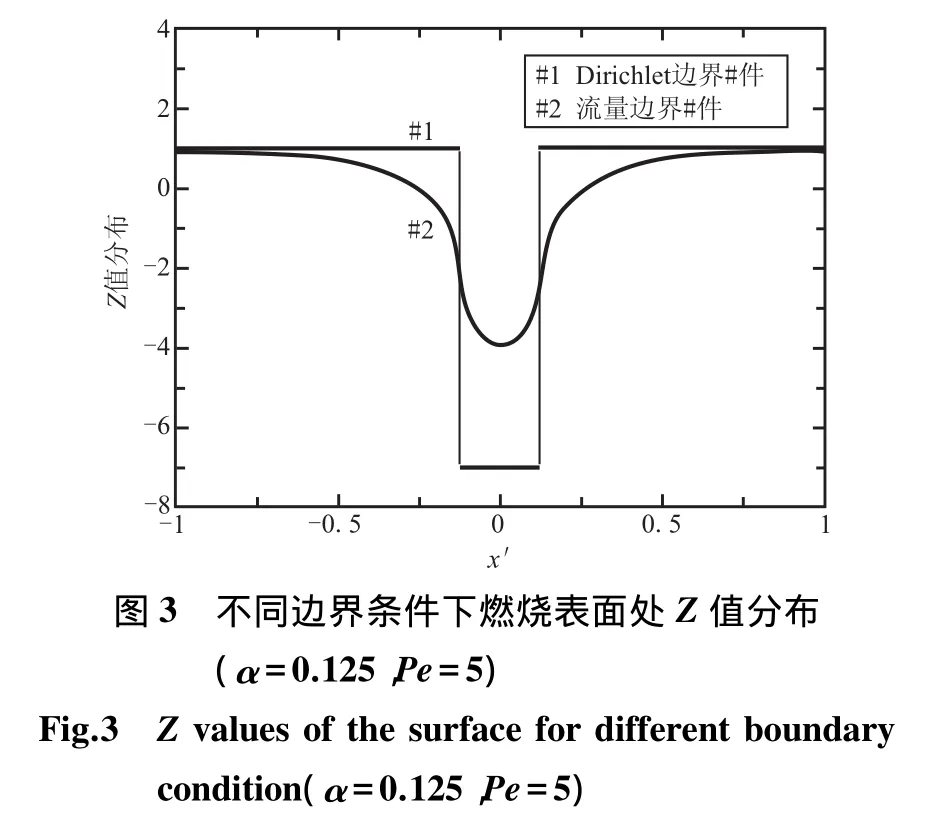
图4给出了采用流量边界时的组分分布，虚线表示化学计量表面SLS。氧化性组分X′穿越化学计量表面SLS出现在粘合剂上方，而粘合剂产物Y′也出现在氧化剂上方。如果不考虑化学反应，仅从组分分布来看，将在粘合剂上方出现富燃预混区，氧化剂上方出现贫燃预混区，而沿着化学计量表面SLS出现弱的扩散火焰区，整个火焰区结构将沿着化学计量表面延伸到燃烧表面。

3.2 化学效应对扩散火焰的影响

图5给出了不同Pe数下的无量纲化学反应速率分布。如果按照Burke－Schumann纯扩散火焰理论，其扩散火焰结构应分布在化学计量表面SLS曲线两侧，并延伸到推进剂表面。但图5表明，该火焰结构仅占据化学计量表面SLS一部分，在SLS曲线之间，出现部分预混的火焰结构。一方面，由于燃烧表面附近温度较低，而不足以使化学反应延伸到燃烧表面，因而出现火焰前沿;另一方面，在火焰前沿与燃烧表面之间，组分X和Y相互扩散混合，在粘合剂上方出现部分预混火焰，最大化学反应速率出现在前沿火焰结构LEF中，该结构在SLS曲线偏向富燃预混区。随着Pe数的增大，对流速率逐渐增强，而扩散混合速率基本不变，组分混合受到抑制，预混火焰区域变薄，扩散火焰高度增加，热释放核心区域的化学反应速率也逐渐增强。

图6给出了不同Da数下的无量纲化学反应速率分布。随着达姆科勒数的增加，化学反应速率逐渐增强，火焰结构逐步靠近燃烧表面;另一方面，随着达姆科勒数的增加，在粘合剂上方所形成的预混化学反应逐渐减弱，合并的前沿火焰结构逐渐分离，形成一个不太明显的三重火焰(Tribrachial or triple flame)［13］的前沿火焰结构LEF，在粘合剂上方，该结构有明显的富燃预混火焰区，但处在氧化剂上方的贫燃预混火焰结构却不明显。气相区的扩散火焰由部分预混的前沿火焰结构LEF和沿着化学计量表面SLS的尾迹扩散火焰组成。当粘合剂含量α为0.2，Pe为10时，Da数的变化并不能改变化学计量表面SLS的位置，但使热释放核心更加集中在前沿火焰结构LEF中，扩散火焰更加集中在化学计量表面SLS两侧。

3.3 粘合剂含量对火焰结构的影响

图7是不同粘合剂含量下的化学反应速率分布。

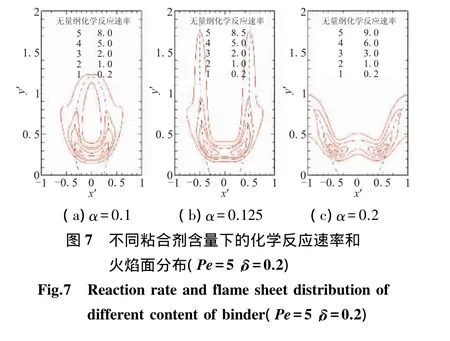
当β=7时，氧化剂和粘合剂的化学计量配比是c=1/(1+β)=0.125，如果粘合剂含量 α＜c，则类似于Burke－Schumann的欠通风情形，如图7(a)所示;如果α＞c，则形成类似于 Burke－Schumann 的过通风情形，如图7(c)所示。同时，随粘合剂含量增加，燃烧表面上方扩散长度尺度增加，扩散混合效果将减弱，粘合剂中心x=0上方的预混化学反应逐渐减弱，扩散火焰结构逐渐延伸到氧化剂中心|x|=1。

3.4 火焰结构对气相热反馈的影响

图8给出了不同Da数下的气相对燃烧表面的无量纲热反馈(∂T′/∂y′)，虚线表示化学计量表面 SLS 与燃烧表面的交点。

气相区的热释放分布呈“W”状，因而气相对燃烧表面的热反馈呈倒“W”的驼峰状，最大热反馈恰好出现在化学计量表面与燃烧表面的交点处，因此在某种程度上说，化学计量表面SLS对气相区域的热反馈有重大影响。由于沿着化学计量表面SLS的尾迹扩散区域的化学反应速率较低且距燃烧表面较远，其作用主要是增加气相区火焰温度，对燃烧表面的热反馈可以忽略;而气相场的热释放核心集中在前沿火焰结构LEF中，且该结构距燃烧表面的距离较近，因此，气相对燃烧表面的热反馈主要由该结构主导。由前述分析知，当粘合剂含量不变时，Pe数决定化学计量表面SLS的位置，而Da数却决定气相对燃烧表面热反馈的大小;当Pe和Da数不变时，粘合剂含量的变化将改变化学计量表面SLS的位置，从而也将影响到燃烧表面的热反馈。因此，它们共同影响着气相区扩散火焰结构，从而影响复合固体推进的燃烧状态。

4 结论

(1)讨论了AP/HTPB复合固体推进剂燃烧过程中，组分扩散输运速率与对流输运速率在同一个量级时，燃烧表面处采用流量边界条件而不是Dirichlet边界条件，化学计量表面SLS与燃烧表面的交点在氧化剂与粘合剂交界面处偏向氧化剂侧，该偏移对气相热反馈有重要影响。

(2)气相区的扩散火焰由部分预混的前沿火焰结构LEF和沿着化学计量表面SLS的尾迹扩散火焰组成，化学反应核心区域出现在前沿火焰结构LEF中。

(3)当粘合剂含量不变时，Pe数增加时，扩散火焰高度增加;当Da数增加时，将改变前沿火焰结构LEF距离燃烧表面的距离，它们共同影响着扩散火焰结构。

［1］Price E W，Sambamurthi J K，Sigman R K，et al.Combustion of ammonium perchlorate polymer sand－wiches［J］.Combustion and Flame，1986，63(63):381－413.

［2］Chorpening T，Knott G M，Brewster M Q.Flame structure and burning rate of ammonium perchlorate/hydroxyl－terminated polybutadiene propellant sandwiches［J］.Proceedings of the Combustion Institute，2000，28(1):847－853.

［3］Ramakrishna P A，Paul P J，Mukunda H S，et al.Combustion of sandwich propellant at low pressures［J］.Proceedings of the Combustion Institute，2005，30(30):2097－2104.

［4］Fitzgerald R P，Genevieve P，Brewster M Q.Flame and surface structure of laminate propellants with coarse and fine ammonium perchlorate［R］.AIAA 2003－1161.

［5］Fitzgerald R P，Brewster M Q.AP/HTPB laminate propellant flame structure:fuel－lean intrinsic instab ility［J］.Proceedings of the Combustion Institute，2007，31(31):2071－2078.

［6］Massa L，Jackson T L，Buckmaster J，et al.Three－dimensional heterogeneous propellant combustion［J］.Proceedings of the Combustion Institute，2002，29(2):2975－2983.

［7］Jia X，Bilger W R.The Burke－Schumann diffusion flame with zero net flux boundary condition［J］.Combustion Science and Technology，1994，99(4):371－376.

［8］Guirao C，Williams F A.A model for aluminum perchlorate deflagration between 20 and 100 atm［J］.AIAA，1971，9(7):1345－1356.

［9］Cai Wei－dong，Thakre P，Yang V.A model of AP/HTPB composite propellant combustion in rocket motor environments［J］.Combustion Science and Technology，2008，180(12):2143－2169.

［10］Gordon S，McBride B J.Computer program for calculation of complex chemical equilibrium compositions and applications［M］.NASA Reference Publication，1994.

［11］Jackson J L，Yao J.An elementary discussion of propellant flame geometry［J］.Combustion and Flame，1999，117(3):541－552.

［12］Buckmaster J.The effects of time－periodic shear on a diffusion flame anchored to a propellant［J］.Combustion and Flame，2000，120(1/2):211－221.

［13］Kioni P N，Rogg B，Bray K C，et al.Flame spread in laminar mixing layers:the triple flame［J］.Combustion and Flame，1993，95(3):276－292.