固体燃料超燃冲压发动机燃烧室流场准一维计算方法研究①

王利和，武志文，迟鸿伟，魏志军，王宁飞

(北京理工大学 宇航学院，北京 100081)

0 引言

固体燃料超燃冲压发动机(Solid Fuel Scramjet)是一种将固体燃料浇注或粘贴在燃烧室内与超声速气流直接燃烧的冲压发动机。关于固体燃料超燃冲压发动机研究的公开文献较少，美国海军研究生院的Witt［1］和Angus［2］在1989年和1991年，对固体燃料超燃冲压发动机概念进行了初步的研究，他们在燃烧室内加入了少量的氢气作为点火炬;以色列理工学院的Ben-Yakar和 Gany 等［3－6］在 1994～1998年间，对固体燃料超燃冲压发动机燃烧室进行了一系列的实验研究，实验证明了固体燃料在超声速气流中能够自燃和维持火焰稳定，并初步给出了平均燃面退移速率和入口气流参数的关系。

固体燃料超燃冲压发动机燃烧室内的燃烧流动是一个典型的非定常问题。利用二维或三维的数值方法，计算超声速燃烧耗时巨大［7］，在初始研究阶段如何利用一维或者准一维方法，将非定常问题简化显得非常重要。Gany［3］提到了燃烧室流场准一维计算方法，但用到的一维方法里，未耦合固体燃料燃面退移速率模型，无法计算沿轴线的燃面推移速率，且无法分析燃烧室参数随着时间的变化情况。本文将燃面推移速率模型耦合到准一维流场计算方法中，由前一时刻的燃烧室直径加上燃面退移速率，得出下一时刻的燃烧室直径，算出每一时刻的边界条件，将非定常问题转化为每一时刻的定常问题。该方法除了能快速计算每一时刻流场参数和燃面推移速率沿轴线的变化情况外，还能研究相关参数随着时间的变化情况。

1 燃烧室模型

Gany等所用到的固体燃料超燃冲压发动机的燃烧室构型如图1所示，其设计理念是火焰稳定区、等直段燃烧室和扩张段燃烧室。本文采用突扩台阶作为火焰稳定区，则计算模型如图2所示，由突扩台阶、等直段燃烧室和扩张段燃烧室构成。

超声速气流从进气道流出后，在突扩台阶处形成回流，同时马赫数增大，台阶处产生的高温低速回流区能起到稳定火焰的作用;同时，回流产生的漩涡在燃烧室内脱落、移动能促进燃气掺混。在燃烧室内近壁面处，高温高速的气流与固体燃料壁面作用，固体燃料融化、分解、燃烧，燃料的化学能转化为内能。由于气流加热造成的总压损失随着马赫数的增大而增大，等截面燃烧室能起到降低马赫数的作用;又由于等截面燃烧室的加热能力有限［8］，等截面燃烧室后需接扩张燃烧室，以提高燃烧室的性能。

2 准一维计算方法

2.1 流动控制方程

如图3所示，已知燃烧室入口气流初值和等式右边的导数值，用四阶龙格库塔法由j节点的气流参数计算出j+1节点的气流参数。由i时刻的燃烧室直径加上燃面退移速率得出(i+1)时刻的燃烧室直径，然后计算(i+1)时刻的初值和边界条件。文中下标j表示沿轴向的空间，下标i表示时间。

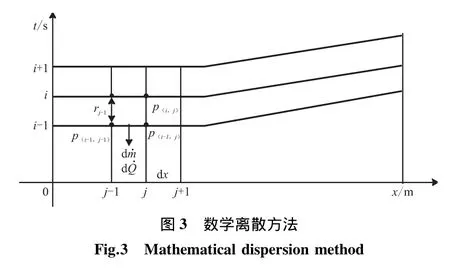
在计算时，有以下几点假设:

(1)燃烧室内气体为理想气体，满足理想气体状态方程。

(2)固体燃料热分解后的气体加入到流场中的速度在1 m/s级别，流场主流速度在1 000 m/s级别，因此忽略燃料加入的动量增量。

(3)固体燃料的燃烧满足化学平衡假设。则式(1)中右边:

式中 f为摩擦系数，f=0.002［3］;De为水力直径;ρf为固体燃料的密度;为j点的燃面退移速率;c为气体p的比定压热容;Q为固体燃料的燃烧热，以有机玻璃(PMMA)为例，参考文献［3］，Q=1×107J/kg。

2.2 燃面退移速率

燃面退移速率的计算方法如式(5)［10］所示:

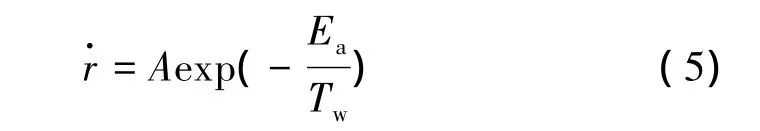
式中 A为指前因子;Ea为活化能;Tw为壁面温度。

对于 PMMA 而言，A=72.1 mm/s，Ea=6 385 J/(mol·K)［11］。壁面温度由近壁面处能量方程计算，近壁面处能量方程为

式中 h为对流换热系数;Tf为近壁面处气体的温度，在准一维方程中，Tf近似为气体的总温;hg为PMMA有效汽化热，hg=1.12×106J/kg［10］;Ts0、ρs和 csp分别为固体燃料的初始温度、密度和比定压热容。

对流换热系数:

式中 λf为气体的热导率;d为内腔的特征长度，对于圆柱体取其内径;Nuf为气体的努塞尔数。

Nuf采用齐德-泰特公式［12］(Sieder-Tate)计算:

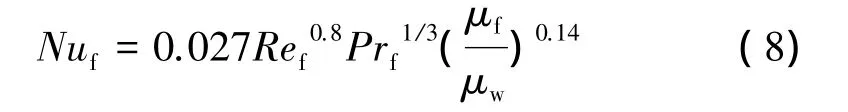
式中 μf和μw是按气体平均温度和壁面温度下的动力粘性系数;Ref和Prf为气体的雷诺数和普朗特数［12］。

μf和 μw由萨特兰公式［13］计算，空气温度为 T 时的动力粘性系数为

式中 μ0为288.15 K时空气的动力粘性系数，μ0=1.789 4×10－5N·s/m2;c 为与气体种类有关的常数，空气的 c=100.4 K。

将图3中j点相关气流参数、燃料物性参数和燃烧尺寸代入式(5)、式(6)中，迭代计算可得到。

2.3 边界条件

(1)燃烧室入口气流参数

如图1所示，燃烧室入口处有突扩台阶，超声速气流经过突扩台阶后有总压损失，由于产生局部损失的情况多种多样及其流动情况的复杂性，对于大多数情况局部损失，只能通过试验来确定［9］。本文通过数值计算，得出突扩台阶的总压恢复系数p02/p01［14］;然后，通过连续方程，得出突扩后的气流参数;表1为进气道出口气流参数;表2为不同台阶面积比下的总压恢复系数。

表1 入口气流条件Table 1 Entrance flow conditions

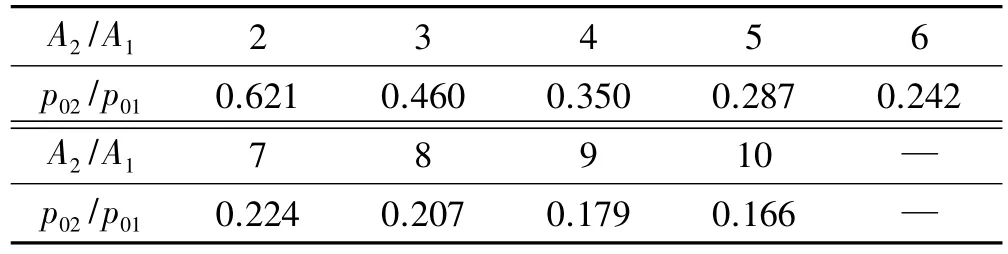
表2 不同A2/A1下的总压恢复系数Table 2 Total pressure recovery coefficient at different A2/A1

将表2中p02/p01与A2/A1的关系拟合成函数得

由进气道出口的总压和面积比代入式(10)，可求出突扩后的气流总压;然后，由连续方程可求出损失后的气流参数。

随着燃烧的进行，燃烧室入口内径发生变化，突扩台阶的面积比会相应发生变化，每一时刻的面积比为

求出相应时刻的突扩台阶面积比，用以上方法可求出该时刻的气流初值。

(2)燃烧室直径

根据给定的燃烧室初始型面尺寸，可得出初始时刻的dA/dx。随着燃烧的进行，燃面退移，由前一时刻的直径加上燃面退移值，得出下一时刻的直径，则下一时刻的燃烧室面积随着轴线的变化由式(12)计算。

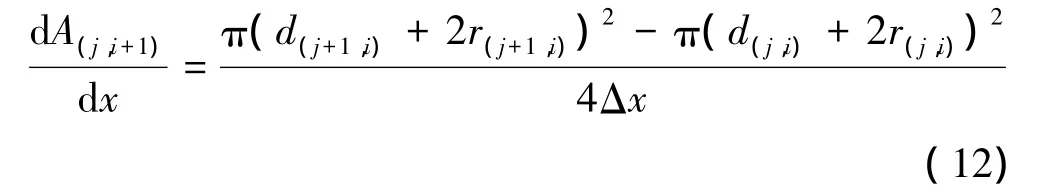
将以上介绍的流场参数和燃面推移速率计算方法编制成计算机程序，程序流程图如图4所示。

2.4 计算方法验证

利用上述方法，对Gany等［3］实验燃烧室进行了计算，结构如图1所示。燃烧室尺寸及燃烧室入口气流参数见文献［3］。

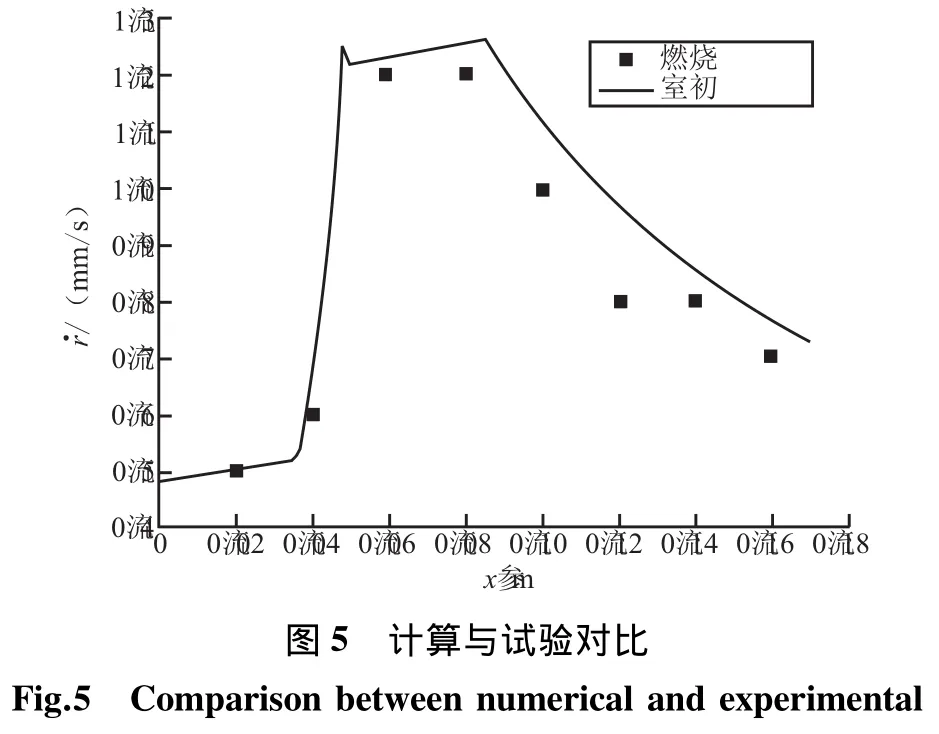
计算了初始时刻燃面退移速率，并和文献［3］中的实验数据进行了对比，如图5所示。从图5可见，计算结果和试验的趋势非常吻合。因为计算时采用化学平衡假设，沿轴线采用固定的燃烧效率，在某些点上误差较大。

3 结果与讨论

流场参数和燃面推移速率计算程序的功能有:

(3)由式(13)计算每一时刻的燃料与空气质量流量的比值(即燃空比)。其中为燃烧室出口质量流量;为入口质量流量。

入口气流参数如表1所示，以R1=13.2mm、R2=R3=26.4mm、L1=155 mm、L2=240 mm、dA=(R3/R2)2=4，工作时间10 s为例。图6是工作过程流场的马赫数，图7是工作过程中燃面推移速率;图8是工作过程中燃空比。

由图6可看出，工作过程中流场马赫数大于1，说明燃烧室维持在超声速燃烧状态。受摩擦和加热等因素的影响，气流马赫数在等直段逐渐下降，合理设计等直段的长度，使气流在等直段出口处马赫数略大于1。扩张段内，加热使气流马赫数降低，面积扩张使马赫数增大，在前段面积扩张的影响大于加热的影响，马赫数增大，在后段加热的影响大于面积扩张的影响，马赫数减小。随着燃面的退移，燃烧室内腔增大，气流膨胀得更厉害，等直段出口马赫数在燃烧室工作过程中逐渐增大。

从图7可看出，在同一时刻内，燃面退移速率先增大，然后趋于平稳。当地燃面退移速率在燃烧室工作过程中逐渐减小。因为燃面退移速率和气流的对流换热系数成正关系，对流换热系数随着气流温度的增大而增大，随着燃烧室直径的增大而减小。在等直段内，气流的温度逐渐上升，燃烧室直径不变。因此，燃面退移速率逐渐增大。在扩张段内，气流温度逐渐上升，而燃烧室直径也逐渐增大，在这2个作用相反的因素作用下，燃面退移速率趋于稳定。随着燃面的退移，燃烧室直径增大，对流换热系数减小。所以，当地燃面退移速率逐渐减小。

从图8可看出，燃空比相对稳定，维持在PMMA的最佳燃空比0.121［3］附近。由图7可看出，燃面退移速率随着时间逐渐较小，而燃面随着时间逐渐增大。因此，工作过程中，沿燃烧室轴向加入燃料质量流量变化不大。

4 结论

(1)将固体燃料燃面退移速率模型耦合到准一维流动方程中。通过独立求解每一时刻的边界条件，将固体燃料超燃冲压发动机燃烧流动这一典型的非定常问题转化为每一时刻的定常问题，从而为固体燃料超燃冲压发动机的燃烧室的初步设计和优化提供了一个快速的计算方法。

(2)燃烧室构型计算结果显示，工作过程中，燃烧室能维持超声速流动;同一时刻内，燃面退移速率沿轴线先增大后趋于稳定，工作过程中，整体燃面退移逐渐减小;由于燃面增大，燃面退移速率减小，工作过程中，燃空比相对稳定。

(3)加热是按照化学平衡假设计算的，如能根据实验数据拟合出合理的加热规律，则计算结果更准确。

［1］Witt M A.Investigation into the feasibility of using solid fuel ramjets for high supersoic/low hypersonic tactical missiles［D］.The USA:Naval Postgraduate School，1989.

［2］Angus W J.An investigation into the performance characteristics of a solid fuel scramjet propulsion dvice［D］.The USA:Naval Postgraduate School，1991.

［3］Ben Y A，Gany A.Experimental study of a solid fuel scramjet［R］.AIAA 94-2815.

［4］Ben Y A，Natan B，Gany A.Investigation of a solid fuel scramjet combustor［J］.Journal of Propulsion and Power，1998，14(4):447-455.

［5］Cohen Z A，Natan B.Experimental investigation of a supersonic combustion solid fuel ramjet［J］.Journal of Propulsion and Power，1998，14(6):880-889.

［6］Ben A R，Spiegler E.Theoretical study of a solid fuel scramjet combustor［J］.Acta Astronautica，1999，45(3):155-166.

［7］王兰，邢建文，郑忠华，等.超燃冲压发动机内流性能的一维评估［J］.推进技术，2008，29(6):641－645.

［8］刘陵，刘敬华，张榛，等.超音速燃烧与超音速燃烧冲压发动机［M］.西安:西北工业大学出版社，1993.

［9］童秉纲，孔祥言，邓国华.气体动力学［M］.北京:高等教育出版社.1989.

［10］夏强.固体燃料冲压发动机工作过程研究［D］.南京:南京理工大学，2011.

［11］Wilde J P de.Fuel pyrolysis effect on hybrid rocket and solid fuel ramjet combustor performance［D］.Netherland:Delft University of Technology，1991.

［12］吉洪湖，张靖周，王锁芳，等.传热学［M］.南京:南京航空航天大学出版社，2004.

［13］王保国，刘淑艳，于勇，等.空气动力学基础［M］.北京:北京理工大学出版社，2008.

［14］Uenishi K，Rogers R C，Northamt G B.Numerical predictions of a rearward－facing－step flow in a supersoic combustor［J］.J.Propulsion，1989，5(2):158－164.

［15］陈灏，胡春波，孙得川，等.固体燃料热分解特性分析［J］.固体火箭技术，2008，31(1).

［16］田辉，蔡国飙，王慧玉，等.固液混合火箭发动机固体燃料的燃速计算［J］.北京航空航天大学学报，2005，31(6).

［17］杨向明，刘伟凯，陈林泉，等.固体燃料超燃冲压发动机原理性实验研究［J］.固体火箭技术，2012，35(3).