动车组修程修制模糊综合评价方法与应用
2013-09-25费良飞王灵芝
费良飞 王 鹏 王灵芝
(1.沈阳地铁集团有限公司运营分公司,110000,沈阳;2.北京交通大学机械与电子控制工程学院,100044,北京;3.中国铁道科学研究院机车车辆研究所,100081,北京∥第一作者,工程师)
动车组的修程、修制主要包括检修规程、检修标准和检修细则(工艺)等基本内容。修程是指机车车辆的修理类型、修理周期(以走行公里、走行时间表示)和具体修理内容。修制主要指机车车辆的检修制度,分为计划预防修理制度和按车辆技术状态的修理制度[1]。
动车组设备复杂、关联性强,受资源限制,对每一设备都进行状态检测并及时修复难度很大,一般是根据不同设备的重要性、可控性和可维修性,科学合理地选择不同的维修方式,形成一套融故障维修、定期维修和状态维修为一体的、优化的综合维修方式[2],以此保证动车组的安全和高效运营。
目前,针对国产高速动车组拟定的修程、修制方案基本上是国外原型动车组修程、修制的简单综合[3],国内在高速动车组运用与维修方面也面临着先期经验匮乏的客观现实,因此其修程、修制是否科学、合理,分析评价方法是否科学、系统,至关重要。此外,评价动车组修程、修制的制定过程及其合理性是一项非常复杂的任务,它受到多种因素的影响,其指标是多种多样的,难于用一项单一指标来度量。
因此,本文提出采用多指标模糊综合评价方法,针对现有修程、修制进行评价和分析,重点探讨可靠性、可用性和经济性等修程、修制决策的影响因素,根据综合评价指标体系确定的原则,进一步建立动车组修程、修制评价指标体系;同时运用模糊综合评价方法对动车组设备重要度进行综合分析,为动车组维修决策提供科学依据。
1 模糊综合评价模型
1.1 模糊综合评价数学模型
模糊综合评判B=A·R是通过模糊评判矩阵(也称模糊关系矩阵)R将运算模糊向量A转变为等级模糊向量B。A·R采取不同的计算模式,可得到不同的综合评判数学模型。一般采用的数学模型(模糊算子)有四种,如表1所示[4]。

表1 四种常用的模糊数学模型
1.2 多层次模糊综合评价模型
当评判系统相当复杂时,需要考虑的因素很多,由此可设计出多层次模糊综合评判模型[5]。多层次模糊综合评判模型的步骤如下。
第一步,将因素集U={u1,u2,…,un}按某些属性分成S个子集合:

其满足条件n1+n2+…+ns=n,U1∪U2∪…∪Us=U,Ui∩Uj=φ(i≠j)。
第二步,对每一子因素集Ui分别作出综合评判。设V={v1,v2,…,vm}为评判集,Ui中各因素相对V的权重分配为:

其中ai1+ai2+…+aint=1。若Ri为单因素评判矩阵,则得出一级评判向量:

第三步,将每个Ui视为一个因素,记μ={U1,U2,…,Us},则μ的单因素评判矩阵为:

每个Ui作为U的一部分,反映了U的某种特性,可按其重要性给出权重分配:

则得到二级向量:

如果每个子因素集Ui仍含有较多因素,可将Ui再行划分,于是有三级模型、四级模型、五级模型等。
2 动车组修程、修制评价体系与指标
2.1 动车组修程、修制评价体系
以修程、修制决策影响因素的综合分析、专家意见及相关国内外资料为基础,根据综合评价指标体系确定的原则,将修程、修制评价体系分为以下三个方面:
(1)可靠性评价。从设备运行过程中的可靠性角度来评价修程、修制。迄今世界范围内并没有统一的评价机车车辆可靠性的指标。综合相关专家经验和各国常用可靠性指标,并结合我国动车组实际运行要求,拟定的影响可靠性的因素包括维修后的预期寿命、平均失效概率、平均无故障时间、完好率、年度运行时间等。此处的运行时间是广义概念,针对不同的设备其含义不同,有的指设备运行时间,有的指设备运行里程[6]。
(2)可用性评价。在工程中,常常根据需要选定产品能工作时间和不能工作时间的不同区间,组成不同的有效度参数。其中使用有效度包含了产品总工作时间内的所有区段,提供了产品处于实际环境条件下的真实有效性度量。因此,它能够反映维修效果的好坏。
(3)经济性评价。维修费用是衡量维修经济性的一个重要指标,也是衡量修程、修制制定得是否合理的重要因素[7],主要包括修复性维修费用、定期预防修费用、状态预防修费用等。其中,每项费用又分别包括维修工时的人工费用、备件费用和后勤保障费用。待工费用分为短期待工费用和长期待工费用。短期待工费用是在设备进行修复性维修时造成短时间的待工而发生的费用。这种短期待工费用主要是对铁路的信誉造成损失、影响未来旅客的多少。长期待工费用包括列车停运造成的收益损失、对旅客的经济赔偿,以及由于列车延误而让旅客选择其他运输方式所花费的费用。设备的故障或不可用性也可能是由于风险事件(事故或偶然事件)造成的,因此发生了风险费用。风险费用分为人员风险费用(例如人员的伤亡)、环境风险费用,以及可能发生的维修、重造费用[8]。
由此,建立了动车组修程、修制评价体系,如图 1所示。

图1 动车组修程、修制评价体系
2.2 评价指标的权重分配
基于三角模糊数加权对数最小二乘法的模型,对评价指标进行权重分配。在群组评价过程中,判断矩阵A中的元素aij有多个值(表示不同人员或小组的意见),且决策者可根据专家经验的多少,赋予每位专家不同的权重,建立对数优化模型[9]:

式中:
b——常数,表示专家或评价小组的数目;
qk——第k个专家或评价小组的权重,由决策者根据各个专家或评价小组的经验丰富程度进行赋值[10]
为求Z的最小值,将式(3)两边对ωp(p=1,2,…,n)取偏导数,并使其等于0。由于化简得到:

考虑个人对待评价事物的判断存在一定的模糊性,采用三角模糊数代替式(4)中的元素,令ωp=(lp, mp,up),apjk= (rpjk,spjk,tpjk),得:
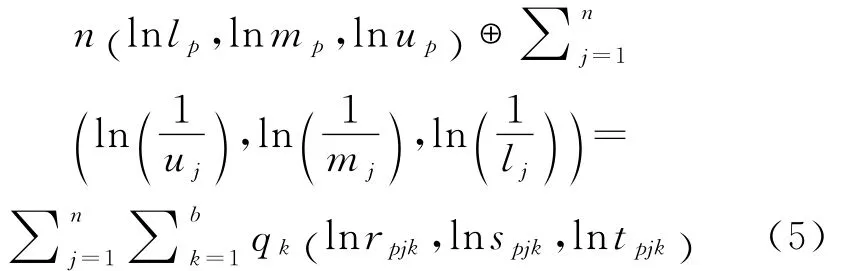
根据三角模糊数的运算规则,由式(5)推导得
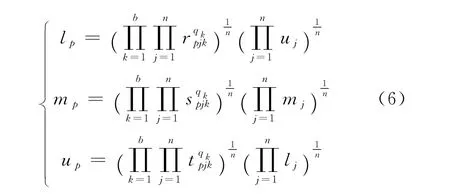

结合式(6)和式(7),由于rijk·tjik=1,可得

wp的左期望值为:右期望值为:I,则 wp的期望值为:

η为乐观-悲观系数。η>0.5,表明决策者是悲观的;η=0.5,表明决策者是中性的;η<0.5,则表明决策者是乐观的。越大,表明与其对应的三角模糊数wp越大。
3 动车组设备重要度模糊综合评价实例
3.1 动车组设备重要度影响因素
对动车组设备进行故障模式和影响分析(FMECA),得到4大类影响设备重要度的因素:可靠性因素(包括设备故障对人员安全性影响、失效对系统功能的影响、失效频率),维修性因素(包括平均修复时间、维修难易程度),经济性因素(维修费用、待工费用),监测性因素(故障可检测性)[11]。在各项因素分析中,考虑到既不使设备重要度评价过于复杂又兼顾评价的精确性,每个影响因素分为4~8个等级。具体评分标准根据表2~7确定,并可在今后根据评价反馈信息和更多的运营经验进行修正。
(1)设备故障对安全性的影响(S):如表2所示。

表2 设备故障等级评分标准
(2)设备失效对动车组系统功能的影响(SF):动车组设备众多,有些设备的失效对安全运行不会产生明显的影响;有些重要设备具有备用件,设备失效也不会对机车的运行造成大的影响;而有些设备故障后必须马上对其进行修理[12]。设备失效对系统功能影响见表3。

表3 失效对系统功能影响评分标准
(3)失效频率:即平均故障率(MFR),如表4所示。平均故障率可根据λ=Nf/∑t计算得到。其中,Nf表示设备在所统计的走行公里或时间内发生的故障总数;∑t表示机车车辆累积走行公里或运行时间[13]。

表4 设备故障概率评分标准
(4)故障可检测性(FD):动车组故障多种多样,有的很容易被发现,有的需要特殊的检测仪器才能检测到,因此,应将设备的可检测性作为影响设备重要度的一个因素。该因素主要考虑检测费用和对检测技术的要求(见表5)。

表5 故障可检测性评分标准
(5)平均修复时间(MTTR):排除故障所需实际修复时间的平均值,即设备修复一次平均需要的时间。排除故障的实际时间包括准备、检测诊断、换件、调校、校验和原件修复等的时间。由于修复时间是随机变量,故MTTR是修复时间的均值或数学期望,即其中表示修复时间t的总和;n表示修复次数[14]。根据德国ICE高速列车的维修指标给出了动车组平均修复时间的评分标准(见表6),在实际应用中可根据具体的车型和维修状况进行修改。

表6 动车组平均修复时间评分标准
(6)维修费用(MC):包括工时费、备件消耗费、后勤保障费等。根据现场记录的维修费用数据,给出了动车组维修费用评分标准(见表7)。

表7 维修费用评分标准
(7)维修难易程度(RD):从维修角度来说,维修难易程度也是影响设备重要度级别的重要因素,其与设备的接近难易程度(包括高度、周围环境)、设备复杂程度和备品备件供应程度有关。其评分标准可通过与现场维修人员讨论确定。
(8)其他影响因素(OTHERS):设备发生临时故障,可能对铁路的信誉造成损失,影响未来客流量;还有对环境造成的影响等。
3.2 重要度评价指数的确定
在确定上述各影响因素的基础上,采用线性加权模型来计算动车组设备重要度评价指数[15]:

式中:
n——影响因素的个数;
mi——对某个被评价设备的第i个影响因素的评分,可根据设备的具体情况和给出的评分标准得到;
βi——第i个影响因素的权重,由权重确定方法得到。
3.3 评价与分析
就8项设备重要度影响因素向三位动车组方面的专家咨询,得到三角模糊判断矩阵如下:
专家1
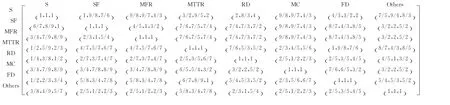
专家2

专家3
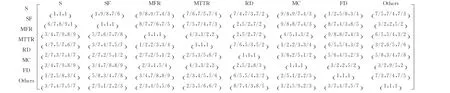
根据2.2节中的方法得到影响因素的权重。再根 据式(9)得到各影响因素权重的期望值,结果见表8。
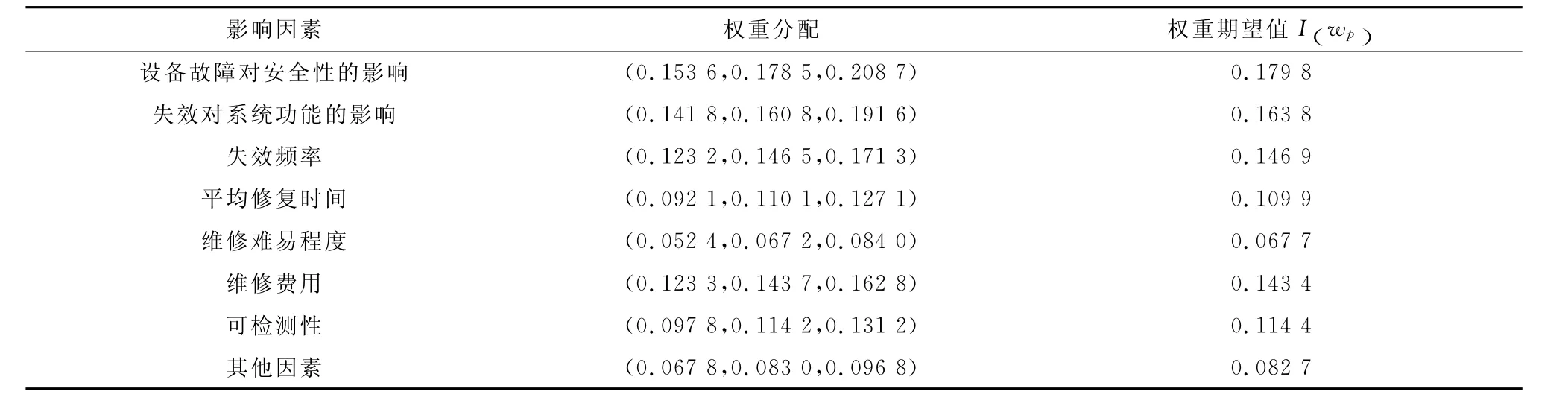
表8 各影响因素的权重分配
根据各设备的运行、维修历史记录以及相关可靠性数据库,按照设备重要度影响因素的评分标准,对每一被评设备的各评价因素进行打分,得到mi的值。根据式(10)可求得设备重要度的排序。以动车组牵引电机、轮对、盘形制动、减振器、车钩和车窗为研究对象,应用上述方法得出其重要度评价指数,如表9所示。

表9 部件重要度得分
目前,动车组的各种运营维修数据和经验相对较少,评价结果尚不够精确;但随着运行时间的增长,可对此评价模型进行改进,以达到更高的评价精度。
4 结语
模糊综合评价法运用模糊数学的思想建立模糊综合评价模型,分析评价指标和影响因素,确定权重分配,计算综合评价值进行综合评判。该方法可应用于多因素的复杂评判系统。
本文运用模糊综合评价方法对动车组设备重要度进行综合评价,并以动车组牵引电机、轮对、盘形制动、减振器、车钩和车窗为研究对象,得出其重要度评价指数。研究表明,牵引电机和车钩的重要度最高,减振器和车窗的重要度最低。该结论可为优化动车组修程、修制提供科学依据。
模糊综合评价方法可有效评价并完善我国动车组修程、修制,其运用的关键在于评价体系的建立和指标权重的分配。然而,各指标数据仍需根据今后的评价反馈信息和更多的运营经验进行修正。
[1]夏胜利,刘芳.国内外铁路机车车辆运用及检修情况对比分析[J].铁道运输与经济,2005(4):39.
[2]张曙光.京沪高速铁路系统优化研究[M].北京:中国铁道出版社,2009.
[3]阮邵勇.国产动车组修程修制评价系统信息编码的研究[D].北京:北京交通大学,2006.
[4]张国立,孔辉,孔倩.模糊数学基础及应用[M].北京:化学工业出版社,2011.
[5](美)坎塔尔季奇.数据挖掘:概念、模型、方法和算法[M].2版.王晓海,译.北京:清华大学出版社,2013.
[6]董锡明.机车车辆维修基本理论[M].北京:中国铁道出版社,2005.
[7]刘刚,王华胜,文礼.高速列车修程修制技术[J].中国铁路,2010(12):62.
[8]陈煜.基于EAM的高速铁路动车段检修作业工单优化模型与方法的研究[D].北京:北京交通大学,2008.
[9]肖明耀.矩阵最小二乘法及其应用[M].北京:中国计量科学研究院,1978.
[10]李登辉.直觉模糊集决策与对策分析方法[M].北京:国防工业出版社,2012.
[11]刘丽影,刘继刚,刘继.我国高速动车组检修制度[J].同济大学学报:自然科学版,2001(8):58.
[12]孙研婷.动车组关键零部件维修决策模型的研究[D].北京:北京交通大学,2012.
[13]王彩霞.高速动车组主要零部件损伤规律及维修周期的研究[D].北京:北京交通大学,2012.
[14]曹新平.国产动车组零部件维修管理信息系统的开发[D].北京:北京交通大学,2008.
[15]曹炳元.应用模糊数学与系统[M].北京:科学出版社,2005.
