铁电薄膜漏电流的应变调控*

文娟辉 杨琼 曹觉先 周益春

1 引言

由于铁电材料具有压电、电光、声光、热释电、光折变和高介电系数等优良特性,铁电材料在铁电随机存取存储器(FRAM)、动态随机存储器(DRAM)、高介电常数电容器、声学器件、热释电探测器等多功能器件具有广泛的应用.特别值得提出的是,由于铁电薄膜材料具有很稳定的化学性能和抗辐射性能强等优点,纳米尺度铁电材料在非易失性FRAMs中具有潜在应用前景.随着薄膜制备技术的发展,在研究铁电薄膜材料的过程中,研究人员发现铁电薄膜比块体材料性能更优良、更容易向实用化方向发展.当铁电薄膜的厚度接近几纳米时,漏电流成了一个决定器件完整性和可靠性的重要指标[1-5].影响铁电薄膜漏电流的因素有很多.例如,李建军等[6]通过La,V共掺杂的Bi4Ti3O12铁电薄膜的溶胶-凝胶法制备及性能测试研究,发现La,V掺杂后薄膜的漏电流密度明显降低,提高了薄膜漏电流特性;Sim˜Oes等[7]研究指出,不同电极对Bi3.25La0.75Ti3O12铁电薄膜的铁电性能和漏电流具有十分大的影响;通过研究BiFeO3多铁性材料的电子输运特性,Seidel等[8]发现可以通过增减铁电畴壁来控制器件的漏电流.漏电流不仅影响器件的保持性能,而且对铁电薄膜中的畴壁运动、缺陷演化、极化强度都具有重要的影响.沈效农和王弘[9]在研究铁电薄膜导电过程与机理时,认为铁电薄膜的极化强度随时间变小时伴随着漏电流逐渐增大,漏电流增加预示着铁电薄膜的电学性质劣化.因此,漏电流是影响铁电薄膜材料性能至关重要的因素.有效抑制铁电薄膜中的漏电流、提高材料的铁电性能是当前铁电材料领域的热点问题.Cheng等[10]通过对磁性隧道结的漏电流研究指出,增加薄膜厚度,漏电流明显减小,整流效应显著加强;贾建峰等[11]在MgO/(Ba0.8Sr0.2)TiO3多层薄膜的介电和漏电特性研究中,发现MgO层的引入改变了(Ba0.8Sr0.2)TiO3的介电特性和漏电流行为,使薄膜的漏电流降低了3个数量级.

本文主要采用第一性原理探讨应变对铁电薄膜漏电流的调控.实际上,由于多层膜的制备,铁电薄膜与衬底及电极之间的界面状态不可避免地会使铁电薄膜存在应变.应变是影响铁电薄膜材料性能的重要因素,尤其是当薄膜的厚度降低到纳米尺度以后,应力对薄膜的形貌、结构、性能、界面处的缺陷和电子密度都会产生至关重要的影响.如果能有效控制铁电薄膜中的应变为我所用,铁电薄膜的物理性能将得到极大提高.Scott[12]指出衬底/铁电薄膜界面和高应变态将是今后的铁电材料的重点研究方向.王彪课题组通过理论研究发现应变会诱发PbTiO3的顺电-铁电相变,并且分别研究了顺电和铁电PbTiO3的输运性质[13,14].极化、畴壁、应变等因素是影响铁电薄膜漏电流的重要因素.在本文中,仅仅以BaTiO3的顺电相为例,采用非平衡格林函数来探讨外加应变对其输运性质的影响及其机理.我们发现压应变能有效抑制漏电流,特别是当压应变为4%时,其漏电流相对于无应变状态降低近10倍.

2 计算方法

本文采用基于密度泛函理论的VASP软件包来实现Pt/BaTiO3/Pt界面结构优化.计算中采用投影缀加波法(PAW)[15]描述离子和电子之间的相互作用,而交换关联函数采用GGA-PBEsol[16];平面波截断动能为450 eV;采用6×6×1 Monkhorst-Pack[17]K点网格;结构优化的收敛标准为所有原子间Hellmann-Feynman力均小于0.005 eV/˚A.

如图1所示,本文构建了以TiO2为终端的Pt/TiO2-(BaO-TiO2)n/Pt三明治界面结构,O原子位于Pt原子的正上方.为了得到顺电相的BaTiO3薄膜,在结构优化的过程中,保持体系关于中心TiO2原子层镜面对称.平面内晶格常数固定在顺电相BaTiO3优化晶格常数3.987˚A,真空层厚度为15˚A.铁电薄膜的漏电流和传输概率的研究采用ATOMISTIX TOOLKIT(ATK)[18]来模拟计算,它是基于密度泛函理论,利用非平衡格林函数方法来处理纳米器件在外置偏压下的电子输运性质.采用的交换关联泛函是GGA-PBE,横向布里渊区积分采用8×8的k点网格.

3 结果分析和讨论

3.1 BaTiO3铁电薄膜的结构分析

为了探索应变对铁电隧道结输运性质的影响,首先构建了一个Pt/TiO2-(BaTiO3)m/Pt的顺电态模型如图1所示(m=5).它分为左电极、中间散射区和右电极,中间散射区是由钛酸钡层和左右电极表层所组成,所研究的钛酸钡模型是以TiO2为终端界面,并且氧原子位于最外层Pt电极的上面.本文考虑的外加应变ε=(as-a0)/as[19],其中as是加应变的铁电隧道结的平面内晶格常数,a0是不加应变时的结构的晶格常数.当加上应变时,产生应变场,平面内晶格常数由a0变为as,而原子位置会沿界面法线方向弛豫[13].

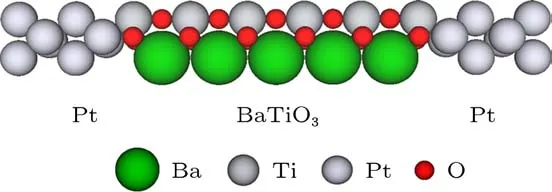
图1 Pt/BaTiO3/Pt的结构示意图

3.2 漏电流

为了研究BaTiO3铁电隧道结在外加应变下的电子输运性质,本文使用ATOMISTIX TOOLKIT(ATK 2008.10)软件包计算不同应变下BaTiO3铁电隧道结的输运性质.在纳米器件中,漏电流可以由Landauer—B¨uttiker表示为[20,21]

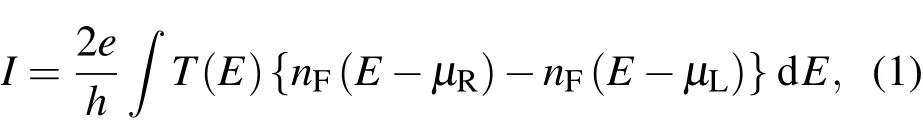
式中µL和µR分别为左右电极的化学势而nF(E)为费米狄拉克分布函数,T(E)为电子的传输概率.当温度为0 K时,漏电流表达式(1)可以简化成

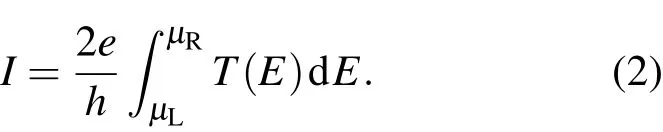
我们主要利用(2)式探讨应变对有限偏压下铁电薄膜漏电流的影响特征.图2分别给出了铁电薄膜应变为ε=-4%,-2%,0,2%,4%时,漏电流随偏压的变化关系.图中的正负号分别对应拉应变和压应变.从图中可以发现,随着拉伸应变的增加,漏电流显著增加,而在压应变状态下,漏电流急剧减小.特别值得提出的是,当压应变ε=-4%时,漏电流相对于无应变状态的铁电薄膜降低近一个数量级,这说明漏电流得到了极大抑制.因此,我们的研究结果显示,可以通过应变来调控铁电薄膜的漏电流,提高铁电薄膜及其器件的电学性能.

铁电薄膜的厚度是影响材料漏电流的一个重要因素,图3给出了钛酸钡薄膜厚度对其漏电流的影响.通过不同厚度下钛酸钡的I-V特征曲线分析,发现随着厚度的增加其漏电流逐渐减小.图3中插图给出了偏压为1 V时,漏电流随钛酸钡层数的变化关系.通过拟合,发现漏电流与薄膜厚度呈现指数变化关系.依据Es-Souni等[22]给出的SCLC导电机制,漏电流与薄膜厚度的关系可表述为I=,其中C,n,m均为常数,I为漏电流密度,d为薄膜厚度,V为电场强度.因此,随着铁电薄膜厚度的增加,漏电流将明显受到抑制.由此可见,要降低铁电薄膜的漏电流,提高铁电薄膜的性能,薄膜厚度不能太小.

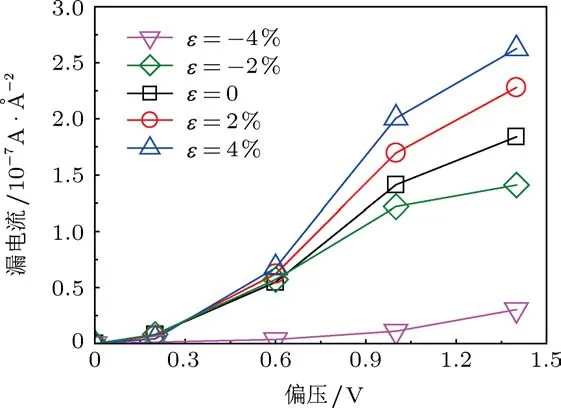
图2 BaTiO3铁电隧道结在不同应变下的漏电流与偏压的关系曲线图

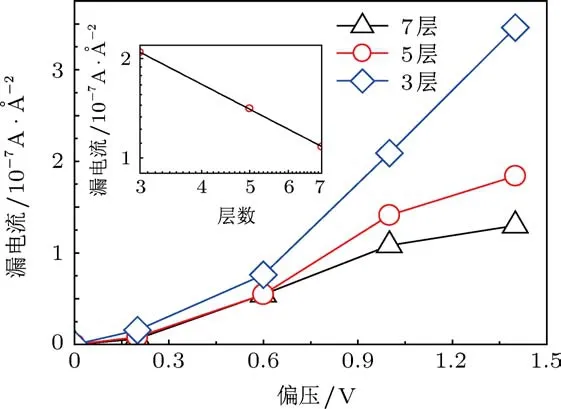
图3 不同钛酸钡层的I-V特征曲线 黑色线、红色线、蓝色线分别表示7层、5层、3层钛酸钡在器件中的I-V特征曲线;插图给出了偏压为1 V时,漏电流随薄膜厚度的变化关系(分别取的对数坐标)

3.3 机理分析

3.3.1 透射系数

为探讨应变影响漏电流机理,我们详细地探讨了不同应变下电子的输运机制.图4给出了不同应变下电子的透射概率.透射系数越大,电子穿过铁电薄膜越容易,漏电流就越大.反之,电子难以穿过铁电薄膜,漏电流就越小.从图中可以发现,在拉伸应变状态下,电子的透射概率幅度相对于无应变状态下有所增加.这意味着电子透射通过铁电薄膜的能力加强,从而导致了在拉伸应变下漏电流增加的主要原因.与拉伸应变状态相反,在压应变状态下,电子的透射概率急剧减小,从而使得压应变状态下铁电薄膜中漏电流受到极大抑制.

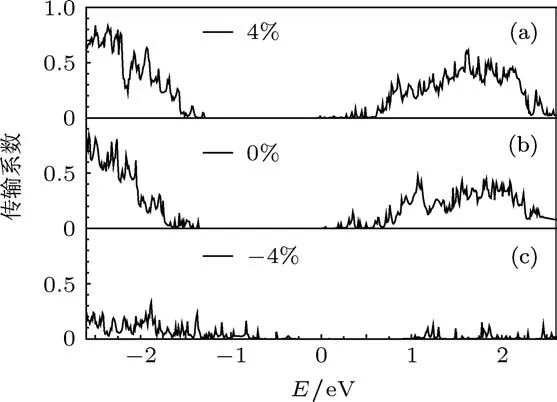
图4 BaTiO3铁电隧道结在零偏压下传输系数与能量的关系(a),(b),(c)分别为5层BaTiO3在应变为4%,0%,-4%时的透射系数,费米能为零

3.3.2 态密度分析

为了解释不同应变下铁电薄膜漏电流的变化,研究了五层钛酸钡薄膜在不同应变下的电子态密度(DOS),如图5所示.图5(a),(b)分别为不同应变下,铁电薄膜内部O原子和Ti的电子态密度.从图中可见,随着拉伸应变的增加,其价带逐渐移向高能区而导带向低能区偏移.这意味着铁电薄膜在拉伸应变状态下,电子带隙将随着拉应变的增加而逐渐减小,从而使得电子穿透本领加强,导致了拉伸应变下铁电薄膜漏电流的增加.然而,当施加压应变时,其价带明显向低能区移动而导带向高能区移动,从而使得电子禁带宽度明显增宽,有效抑制了电子由价带激发到导带的概率.

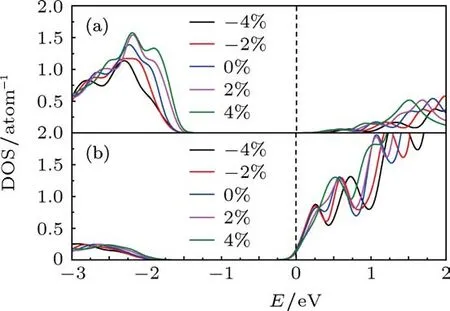
图5 (a),(b)分别为不同应变下,铁电薄膜内部O2,铁电薄膜内部Ti的DOS图

4 结论

结合非平衡格林函数,采用基于密度泛函理论的第一性原理方法,以BaTiO3薄膜为例系统研究了双轴应变对铁电薄膜漏电流的影响.研究结果表明,张应变会使铁电薄膜的漏电流增大,而压应变可以减小铁电薄膜漏电流,从而提高铁电薄膜的保持性能.双轴应变对铁电薄膜漏电流的调控机理来源于：1)在压应变状态下,电子穿透铁电薄膜的本领受到极大抑制;2)当施加压应变时,电子的禁带宽度明显增宽,有效抑制了电子由价带激发到导带的概率.我们的研究表明了双轴应变对铁电薄膜漏电流具有调控作用,这些结论对提高铁电薄膜及铁电存储器的性能,有重要的理论意义和应用价值.

[1]Yang Y,Zhang S R,Liu J S,Zhang H W,Liu M 2006 Insulating Mater.39 51(in Chinese)[杨艳,张树人,刘敬松,张洪伟,刘蒙2006绝缘材料39 51]

[2]Velev J P,Duan C G,Belashchenko K D,Jaswal S S,Tsymbal E Y 2007 Phys.Rev.Lett.98 137201

[3]Tsymbal E Y,Kohlstedt H 2006 Science 313 181

[4]Wang H 2004 Acta Phys.Sin.53 1265(in Chinese)[王华2004物理学报53 1265]

[5]Wang Y L,Wei T R,Liu B T,Deng Z C 2007 Acta Phys.Sin.56 2931(in Chinese)[王英龙,魏同茹,刘保亭,邓泽超2007物理学报56 2931]

[6]Li J J,Yu J,Li J,Wang M,Li Y B,Wu Y Y,Gao J X,Wang Y B 2010 Acta Phys.Sin.59 1302(in Chinese)[李建军,于军,李佳,王梦,李玉斌,吴云翼,高俊雄,王耘波2010物理学报59 1302]

[7]Sim˜oes A Z,Ram´ırez M A,Longo E,Varela J A 2008 Mater.Chem.Phys.107 72

[8]Seidel J,Martin L W,He Q,Zhan Q,Chu Y H,Rother A,Hawkridge M E,Maksymovych P,Yu P,Gajek M,Balke N,Kalinin S V,Gemming S,Wang F,Catalan G,Scott J F,Spaldin N A,Orenstein J,Ramesh R 2009 Nat.Mater.8 229

[9]Shen X N,Wang H 1996 Funct.Mater.27 295(in Chinese)[沈效农,王弘1996功能材料27 295]

[10]Cheng H G,Liu Z L,Yao K L 2011 Appl.Phys.Lett.98 172107

[11]Jia J F,Huang K,Pan Q T,Li S G,He D Y 2006 Acta Phys.Sin.55 2069(in Chinese)[贾建峰,黄凯,潘清涛,李世国,贺德衍2006物理学报55 2069]

[12]Scott J F 2007 Science 315 954

[13]Luo X,Lin S P,Wang B,Zheng Y 2010 Appl.Phys.Lett.97 012905

[14]Luo X,Wang B,Zheng Y 2011 ACS Nano 5 1649

[15]Kresse G,Joubert D 1999 Phys.Rev.B 59 1758

[16]Perdew J P,Ruzsinszky A,Csonka G I,Vydrov O A,Scuseria G E,Constantin L A,Zhou X L,Burke K 2008 Phys.Rev.Lett.100 136406

[17]Monkhorst H J,Pack J D 1976 Phys.Rev.B 13 5188

[18]Brandbyge M,Mozos J L,Ordej´on P,Taylor J,Stokbro K 2002 Phys.Rev.B 65 165401

[19]Pertsev N A,Zembilgotov A G,Tagantsev A K 1998 Phys.Rev.Lett.80 1988

[20]DattaS1995ElectronicTransportinMesoscopicSystems(Cambridge：Cambridge University Press)p7

[21]Luo X,Wang B,Zheng Y 2009 J.Appl.Phys.106 073711

[22]Es-Souni M,Zhang N,Iakovlev S,Solterbeck C H,Piorra A 2003 Thin Solid Films 440 26